13: Temperature, Kinetic Theory, and the Gas Laws (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
13.1: Temperature
1. What does it mean to say that two systems are in thermal equilibrium?
2. Give an example of a physical property that varies with temperature and describe how it is used to measure temperature.
3. When a cold alcohol thermometer is placed in a hot liquid, the column of alcohol goes down slightly before going up. Explain why.
4. If you add boiling water to a cup at room temperature, what would you expect the final equilibrium temperature of the unit to be? You will need to include the surroundings as part of the system. Consider the zeroth law of thermodynamics.
13.2: Thermal Expansion of Solids and Liquids
5. Thermal stresses caused by uneven cooling can easily break glass cookware. Explain why Pyrex®, a glass with a small coefficient of linear expansion, is less susceptible.
6. Water expands significantly when it freezes: a volume increase of about 9% occurs. As a result of this expansion and because of the formation and growth of crystals as water freezes, anywhere from 10% to 30% of biological cells are burst when animal or plant material is frozen. Discuss the implications of this cell damage for the prospect of preserving human bodies by freezing so that they can be thawed at some future date when it is hoped that all diseases are curable.
7. One method of getting a tight fit, say of a metal peg in a hole in a metal block, is to manufacture the peg slightly larger than the hole. The peg is then inserted when at a different temperature than the block. Should the block be hotter or colder than the peg during insertion? Explain your answer.
8. Does it really help to run hot water over a tight metal lid on a glass jar before trying to open it? Explain your answer.
9. Liquids and solids expand with increasing temperature, because the kinetic energy of a body’s atoms and molecules increases. Explain why some materials shrink with increasing temperature.
13.3: The Ideal Gas Law
10. Find out the human population of Earth. Is there a mole of people inhabiting Earth? If the average mass of a person is 60 kg, calculate the mass of a mole of people. How does the mass of a mole of people compare with the mass of Earth?
11. Under what circumstances would you expect a gas to behave significantly differently than predicted by the ideal gas law?
12. A constant-volume gas thermometer contains a fixed amount of gas. What property of the gas is measured to indicate its temperature?
13.4: Kinetic Theory: Atomic and Molecular Explanation of Pressure and Temperature
13. How is momentum related to the pressure exerted by a gas? Explain on the atomic and molecular level, considering the behavior of atoms and molecules.
13.5: Phase Changes
14. A pressure cooker contains water and steam in equilibrium at a pressure greater than atmospheric pressure. How does this greater pressure increase cooking speed?
15. Why does condensation form most rapidly on the coldest object in a room—for example, on a glass of ice water?
16. What is the vapor pressure of solid carbon dioxide (dry ice) at –78.5ºC?
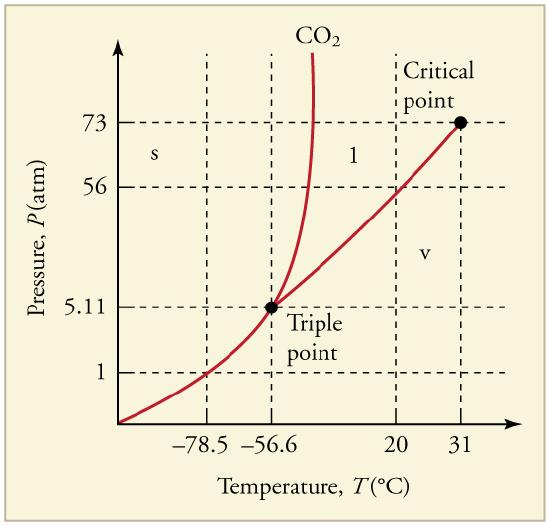
The phase diagram for carbon dioxide. The axes are nonlinear, and the graph is not to scale. Dry ice is solid carbon dioxide and has a sublimation temperature of –78.5ºC.
17. Can carbon dioxide be liquefied at room temperature (20ºC)? If so, how? If not, why not? (See Figure.)
18. Oxygen cannot be liquefied at room temperature by placing it under a large enough pressure to force its molecules together. Explain why this is.
19. What is the distinction between gas and vapor?
13.6: Humidity, Evaporation, and Boiling
20. Because humidity depends only on water’s vapor pressure and temperature, are the saturation vapor densities listed in Table valid in an atmosphere of helium at a pressure of 1.01×105N/m2, rather than air? Are those values affected by altitude on Earth?
21. Why does a beaker of 40.0ºC water placed in a vacuum chamber start to boil as the chamber is evacuated (air is pumped out of the chamber)? At what pressure does the boiling begin? Would food cook any faster in such a beaker?
22. Why does rubbing alcohol evaporate much more rapidly than water at STP (standard temperature and pressure)?
Problems & Exercises
13.1: Temperature
23. What is the Fahrenheit temperature of a person with a 39.0ºC fever?
Solution
102ºF
24. Frost damage to most plants occurs at temperatures of 28.0ºF or lower. What is this temperature on the Kelvin scale?
25. To conserve energy, room temperatures are kept at 68.0ºF in the winter and 78.0ºF in the summer. What are these temperatures on the Celsius scale?
Solution
20.0ºC and 25.6ºC
26. A tungsten light bulb filament may operate at 2900 K. What is its Fahrenheit temperature? What is this on the Celsius scale?
27. The surface temperature of the Sun is about 5750 K. What is this temperature on the Fahrenheit scale?
Solution
9890ºF
28. One of the hottest temperatures ever recorded on the surface of Earth was 134ºF in Death Valley, CA. What is this temperature in Celsius degrees? What is this temperature in Kelvin?
29. (a) Suppose a cold front blows into your locale and drops the temperature by 40.0 Fahrenheit degrees. How many degrees Celsius does the temperature decrease when there is a 40.0ºF decrease in temperature?
(b) Show that any change in temperature in Fahrenheit degrees is nine-fifths the change in Celsius degrees.
Solution
(a) 22.2ºC
(b) ΔT(ºF)=T2(ºF)−T1(ºF)
=95T2(ºC)+32.0º−(95T1(ºC)+32.0º)
=95(T2(ºC)−T1(ºC))=95ΔT(ºC)
30. (a) At what temperature do the Fahrenheit and Celsius scales have the same numerical value?
(b) At what temperature do the Fahrenheit and Kelvin scales have the same numerical value?
13.2: Thermal Expansion of Solids and Liquids
31. The height of the Washington Monument is measured to be 170 m on a day when the temperature is 35.0ºC. What will its height be on a day when the temperature falls to −10.0ºC? Although the monument is made of limestone, assume that its thermal coefficient of expansion is the same as marble’s.
Solution
169.95 m
32. How much taller does the Eiffel Tower become at the end of a day when the temperature has increased by 15ºC? Its original height is 321 m and you can assume it is made of steel.
33. What is the change in length of a 3.00-cm-long column of mercury if its temperature changes from 37.0ºC to 40.0ºC, assuming the mercury is unconstrained?
Solution
5.4×10−6m
34. How large an expansion gap should be left between steel railroad rails if they may reach a maximum temperature 35.0ºC greater than when they were laid? Their original length is 10.0 m.
35. You are looking to purchase a small piece of land in Hong Kong. The price is “only” $60,000 per square meter! The land title says the dimensions are 20m×30m. By how much would the total price change if you measured the parcel with a steel tape measure on a day when the temperature was 20ºC above normal?
Solution
Because the area gets smaller, the price of the land DECREASES by $17,000.
36. Global warming will produce rising sea levels partly due to melting ice caps but also due to the expansion of water as average ocean temperatures rise. To get some idea of the size of this effect, calculate the change in length of a column of water 1.00 km high for a temperature increase of 1.00ºC. Note that this calculation is only approximate because ocean warming is not uniform with depth.
37. Show that 60.0 L of gasoline originally at 15.0ºC size 12{"15" "." 0°C} {} will expand to 61.1 L when it warms to 35.0ºC, size 12{"35" "." 0°"C,"} {} as claimed in Example.
Solution
V=V0+ΔV=V0(1+βΔT)
=(60.00L)[1+(950×10−6/ºC)(35.0ºC−15.0ºC)]
=61.1L
38. (a) Suppose a meter stick made of steel and one made of invar (an alloy of iron and nickel) are the same length at 0ºC. What is their difference in length at 22.0ºC?
(b) Repeat the calculation for two 30.0-m-long surveyor’s tapes.
39. (a) If a 500-mL glass beaker is filled to the brim with ethyl alcohol at a temperature of 5.00ºC, how much will overflow when its temperature reaches 22.0ºC?
(b) How much less water would overflow under the same conditions?
Solution
(a) 9.35 mL
(b) 7.56 mL
40. Most automobiles have a coolant reservoir to catch radiator fluid that may overflow when the engine is hot. A radiator is made of copper and is filled to its 16.0-L capacity when at 10.0ºC. What volume of radiator fluid will overflow when the radiator and fluid reach their 95.0ºC operating temperature, given that the fluid’s volume coefficient of expansion is β=400×10–6/ºC? Note that this coefficient is approximate, because most car radiators have operating temperatures of greater than 95.0ºC.
41. A physicist makes a cup of instant coffee and notices that, as the coffee cools, its level drops 3.00 mm in the glass cup. Show that this decrease cannot be due to thermal contraction by calculating the decrease in level if the 350cm3 of coffee is in a 7.00-cm-diameter cup and decreases in temperature from 95.0ºC to 45.0ºC. (Most of the drop in level is actually due to escaping bubbles of air.)
Solution
0.832 mm
42. (a) The density of water at 0ºC is very nearly 1000kg/m3 (it is actually 999.84kg/m3), whereas the density of ice at 0ºC is 917kg/m3. Calculate the pressure necessary to keep ice from expanding when it freezes, neglecting the effect such a large pressure would have on the freezing temperature. (This problem gives you only an indication of how large the forces associated with freezing water might be.)
(b) What are the implications of this result for biological cells that are frozen?
43. Show that β≈3α, by calculating the change in volume ΔV of a cube with sides of length L.
Solution
We know how the length changes with temperature: ΔL=αL0ΔT. Also we know that the volume of a cube is related to its length by V=L3 , so the final volume is then V=V0+ΔV=(L0+ΔL)3. Substituting for ΔL gives
V=(L0+αL0ΔT)3=L30(1+αΔT)3.
Now, because αΔT is small, we can use the binomial expansion:
V≈L30(1+3αΔT)=L30+3αL30ΔT.
So writing the length terms in terms of volumes gives V=V0+ΔV≈V0+3αV0ΔT, and so
ΔV=βV0ΔT≈3αV0ΔT, or β≈3α.
13.3: The Ideal Gas Law
44. The gauge pressure in your car tires is 2.50×105N/m2 at a temperature of 35.0ºC when you drive it onto a ferry boat to Alaska. What is their gauge pressure later, when their temperature has dropped to –40.0ºC?
Solution
1.623 atm
45. Convert an absolute pressure of 7.00×105N/m2 to gauge pressure in lb/in2. (This value was stated to be just less than 90.0lb/in2 in Example. Is it?)
46. Suppose a gas-filled incandescent light bulb is manufactured so that the gas inside the bulb is at atmospheric pressure when the bulb has a temperature of 20.0ºC.
(a) Find the gauge pressure inside such a bulb when it is hot, assuming its average temperature is 60.0ºC (an approximation) and neglecting any change in volume due to thermal expansion or gas leaks.
(b) The actual final pressure for the light bulb will be less than calculated in part (a) because the glass bulb will expand. What will the actual final pressure be, taking this into account? Is this a negligible difference?
Solution
(a) 0.136 atm
(b) 0.135 atm. The difference between this value and the value from part (a) is negligible.
47. Large helium-filled balloons are used to lift scientific equipment to high altitudes.
(a) What is the pressure inside such a balloon if it starts out at sea level with a temperature of 10.0ºC and rises to an altitude where its volume is twenty times the original volume and its temperature is –50.0ºC?
(b) What is the gauge pressure? (Assume atmospheric pressure is constant.)
48. Confirm that the units of nRT are those of energy for each value of R:
(a) 8.31J/mol⋅K,
(b) 1.99cal/mol⋅K, and
(c) 0.0821L⋅atm/mol⋅K.
Solution
(a) nRT=(mol)(J/mol⋅K)(K)=J
(b) nRT=(mol)(cal/mol⋅K)(K)=cal
(c) nRT=(mol)(L⋅atm/mol⋅K)(K)
=L⋅atm=(m3)(N/m2)
=N⋅m=J
49. In the text, it was shown that N/V=2.68×1025m−3 for gas at STP.
(a) Show that this quantity is equivalent to N/V=2.68×1019cm−3, as stated.
(b) About how many atoms are there in one μm3 (a cubic micrometer) at STP?
(c) What does your answer to part (b) imply about the separation of atoms and molecules?
50. Calculate the number of moles in the 2.00-L volume of air in the lungs of the average person. Note that the air is at 37.0ºC (body temperature).
Solution
7.86×10−2mol
51. An airplane passenger has 100cm3 of air in his stomach just before the plane takes off from a sea-level airport. What volume will the air have at cruising altitude if cabin pressure drops to 7.50×104N/m2?
52. (a) What is the volume (in km3) of Avogadro’s number of sand grains if each grain is a cube and has sides that are 1.0 mm long? (b) How many kilometers of beaches in length would this cover if the beach averages 100 m in width and 10.0 m in depth? Neglect air spaces between grains.
Solution
(a) 6.02×105km3
(b) 6.02×108km
53. An expensive vacuum system can achieve a pressure as low as 1.00×10–7N/m2 at 20ºC. How many atoms are there in a cubic centimeter at this pressure and temperature?
54. The number density of gas atoms at a certain location in the space above our planet is about 1.00×1011m−3, and the pressure is 2.75×10–10N/m2 in this space. What is the temperature there?
Solution
−73.9ºC
55. A bicycle tire has a pressure of 7.00×105N/m2 at a temperature of 18.0ºC and contains 2.00 L of gas. What will its pressure be if you let out an amount of air that has a volume of 100cm3 at atmospheric pressure? Assume tire temperature and volume remain constant.
56. A high-pressure gas cylinder contains 50.0 L of toxic gas at a pressure of 1.40×107N/m2 and a temperature of 25.0ºC. Its valve leaks after the cylinder is dropped. The cylinder is cooled to dry ice temperature (–78.5ºC) to reduce the leak rate and pressure so that it can be safely repaired.
(a) What is the final pressure in the tank, assuming a negligible amount of gas leaks while being cooled and that there is no phase change?
(b) What is the final pressure if one-tenth of the gas escapes?
(c) To what temperature must the tank be cooled to reduce the pressure to 1.00 atm (assuming the gas does not change phase and that there is no leakage during cooling)?
(d) Does cooling the tank appear to be a practical solution?
Solution
(a) 9.14×106N/m2
(b) 8.23×106N/m2
(c) 2.16 K
(d) No. The final temperature needed is much too low to be easily achieved for a large object.
57. Find the number of moles in 2.00 L of gas at 35.0ºC and under 7.41×107N/m2 of pressure.
58. Calculate the depth to which Avogadro’s number of table tennis balls would cover Earth. Each ball has a diameter of 3.75 cm. Assume the space between balls adds an extra 25.0% to their volume and assume they are not crushed by their own weight.
Solution
41 km
59. (a) What is the gauge pressure in a 25.0ºC car tire containing 3.60 mol of gas in a 30.0 L volume?
(b) What will its gauge pressure be if you add 1.00 L of gas originally at atmospheric pressure and 25.0ºC? Assume the temperature returns to 25.0ºC and the volume remains constant.
60. (a) In the deep space between galaxies, the density of atoms is as low as 106atoms/m3, and the temperature is a frigid 2.7 K. What is the pressure?
(b) What volume (in m3) is occupied by 1 mol of gas?
(c) If this volume is a cube, what is the length of its sides in kilometers?
Solution
(a) 3.7×10−17Pa
(b) 6.0×1017m3
(c) 8.4×102km
13.4: Kinetic Theory: Atomic and Molecular Explanation of Pressure and Temperature
61. Some incandescent light bulbs are filled with argon gas. What is vrms for argon atoms near the filament, assuming their temperature is 2500 K?
Solution
1.25×103m/s
62. Average atomic and molecular speeds (vrms) are large, even at low temperatures. What is vrms for helium atoms at 5.00 K, just one degree above helium’s liquefaction temperature?
63. (a) What is the average kinetic energy in joules of hydrogen atoms on the 5500ºC surface of the Sun?
(b) What is the average kinetic energy of helium atoms in a region of the solar corona where the temperature is 6.00×105K?
Solution
(a) 1.20×10−19J
(b) 1.24×10−17J
64. The escape velocity of any object from Earth is 11.2 km/s.
(a) Express this speed in m/s and km/h.
(b) At what temperature would oxygen molecules (molecular mass is equal to 32.0 g/mol) have an average velocity vrms equal to Earth’s escape velocity of 11.1 km/s?
65. The escape velocity from the Moon is much smaller than from Earth and is only 2.38 km/s. At what temperature would hydrogen molecules (molecular mass is equal to 2.016 g/mol) have an average velocity vrms equal to the Moon’s escape velocity?
Solution
458K
66. Nuclear fusion, the energy source of the Sun, hydrogen bombs, and fusion reactors, occurs much more readily when the average kinetic energy of the atoms is high—that is, at high temperatures. Suppose you want the atoms in your fusion experiment to have average kinetic energies of 6.40×10–14J. What temperature is needed?
67. Suppose that the average velocity (vrms) of carbon dioxide molecules (molecular mass is equal to 44.0 g/mol) in a flame is found to be 1.05×105m/s. What temperature does this represent?
Solution
1.95×107K
68. Hydrogen molecules (molecular mass is equal to 2.016 g/mol) have an average velocity vrms equal to 193 m/s. What is the temperature?
69. Much of the gas near the Sun is atomic hydrogen. Its temperature would have to be 1.5×107K for the average velocity vrms to equal the escape velocity from the Sun. What is that velocity?
Solution
6.09×105m/s
70. There are two important isotopes of uranium— 235U and 238U; these isotopes are nearly identical chemically but have different atomic masses. Only 235U is very useful in nuclear reactors. One of the techniques for separating them (gas diffusion) is based on the different average velocities vrms of uranium hexafluoride gas, UF6.
(a) The molecular masses for 235U UF6 and 238U UF6 are 349.0 g/mol and 352.0 g/mol, respectively. What is the ratio of their average velocities?
(b) At what temperature would their average velocities differ by 1.00 m/s?
(c) Do your answers in this problem imply that this technique may be difficult?
13.6: Humidity, Evaporation, and Boiling
71. Dry air is 78.1% nitrogen. What is the partial pressure of nitrogen when the atmospheric pressure is 1.01×105N/m2?
Solution
7.89×104Pa
72. (a) What is the vapor pressure of water at 20.0ºC?
(b) What percentage of atmospheric pressure does this correspond to?
(c) What percent of 20.0ºC air is water vapor if it has 100% relative humidity? (The density of dry air at 20.0ºC is 1.20kg/m3.)
73. Pressure cookers increase cooking speed by raising the boiling temperature of water above its value at atmospheric pressure.
(a) What pressure is necessary to raise the boiling point to 120.0ºC?
(b) What gauge pressure does this correspond to?
Solution
(a) 1.99×105Pa
(b) 0.97 atm
74. (a) At what temperature does water boil at an altitude of 1500 m (about 5000 ft) on a day when atmospheric pressure is 8.59×104N/m2?
(b) What about at an altitude of 3000 m (about 10,000 ft) when atmospheric pressure is 7.00×104N/m2?
75. What is the atmospheric pressure on top of Mt. Everest on a day when water boils there at a temperature of 70.0ºC?
Solution
3.12×104Pa
76. At a spot in the high Andes, water boils at 80.0ºC, greatly reducing the cooking speed of potatoes, for example. What is atmospheric pressure at this location?
77. What is the relative humidity on a 25.0ºC day when the air contains 18.0g/m3 of water vapor?
Solution
78.3%
78. What is the density of water vapor in g/m3 on a hot dry day in the desert when the temperature is 40.0ºC and the relative humidity is 6.00%?
79. A deep-sea diver should breathe a gas mixture that has the same oxygen partial pressure as at sea level, where dry air contains 20.9% oxygen and has a total pressure of 1.01×105N/m2.
(a) What is the partial pressure of oxygen at sea level?
(b) If the diver breathes a gas mixture at a pressure of 2.00×106N/m2, what percent oxygen should it be to have the same oxygen partial pressure as at sea level?
Solution
(a) 2.12×104Pa
(b) 1.06
80. The vapor pressure of water at 40.0ºC is 7.34×103N/m2. Using the ideal gas law, calculate the density of water vapor in g/m3 that creates a partial pressure equal to this vapor pressure. The result should be the same as the saturation vapor density at that temperature (51.1g/m3).
81. Air in human lungs has a temperature of 37.0ºC and a saturation vapor density of 44.0g/m3.
(a) If 2.00 L of air is exhaled and very dry air inhaled, what is the maximum loss of water vapor by the person?
(b) Calculate the partial pressure of water vapor having this density, and compare it with the vapor pressure of 6.31×103N/m2.
Solution
(a) 8.80×10−2g
(b) 6.30×103Pa; the two values are nearly identical.
82. If the relative humidity is 90.0% on a muggy summer morning when the temperature is 20.0ºC, what will it be later in the day when the temperature is 30.0ºC, assuming the water vapor density remains constant?
83. Late on an autumn day, the relative humidity is 45.0% and the temperature is 20.0ºC. What will the relative humidity be that evening when the temperature has dropped to 10.0ºC, assuming constant water vapor density?
Solution
82.3%
84. Atmospheric pressure atop Mt. Everest is .30×104N/m2.
(a) What is the partial pressure of oxygen there if it is 20.9% of the air?
(b) What percent oxygen should a mountain climber breathe so that its partial pressure is the same as at sea level, where atmospheric pressure is 1.01×105N/m2?
(c) One of the most severe problems for those climbing very high mountains is the extreme drying of breathing passages. Why does this drying occur?
85. What is the dew point (the temperature at which 100% relative humidity would occur) on a day when relative humidity is 39.0% at a temperature of 20.0ºC ?
Solution
4.77ºC
86. On a certain day, the temperature is 25.0ºC and the relative humidity is 90.0%. How many grams of water must condense out of each cubic meter of air if the temperature falls to 15.0ºC? Such a drop in temperature can, thus, produce heavy dew or fog.
87. Integrated Concepts
The boiling point of water increases with depth because pressure increases with depth. At what depth will fresh water have a boiling point of 150ºC, if the surface of the water is at sea level?
Solution
38.3m
88. Integrated Concepts
(a) At what depth in fresh water is the critical pressure of water reached, given that the surface is at sea level?
(b) At what temperature will this water boil?
(c) Is a significantly higher temperature needed to boil water at a greater depth?
89. Integrated Concepts
To get an idea of the small effect that temperature has on Archimedes’ principle, calculate the fraction of a copper block’s weight that is supported by the buoyant force in 0ºC water and compare this fraction with the fraction supported in 95.0ºC water.
Solution
(FB/wCu)(FB/wCu)′=1.02. The buoyant force supports nearly the exact same amount of force on the copper block in both circumstances.
90. Integrated Concepts
If you want to cook in water at 150ºC, you need a pressure cooker that can withstand the necessary pressure.
(a) What pressure is required for the boiling point of water to be this high?
(b) If the lid of the pressure cooker is a disk 25.0 cm in diameter, what force must it be able to withstand at this pressure?
91. Unreasonable Results
(a) How many moles per cubic meter of an ideal gas are there at a pressure of 1.00×1014N/m2 and at 0ºC?
(b) What is unreasonable about this result?
(c) Which premise or assumption is responsible?
Solution
(a) 4.41×1010mol/m3
(b) It’s unreasonably large.
(c) At high pressures such as these, the ideal gas law can no longer be applied. As a result, unreasonable answers come up when it is used.
92. Unreasonable Results
(a) An automobile mechanic claims that an aluminum rod fits loosely into its hole on an aluminum engine block because the engine is hot and the rod is cold. If the hole is 10.0% bigger in diameter than the 22.0ºC rod, at what temperature will the rod be the same size as the hole?
(b) What is unreasonable about this temperature? (c) Which premise is responsible?
93. Unreasonable Results
The temperature inside a supernova explosion is said to be 2.00×1013K.
(a) What would the average velocity vrms of hydrogen atoms be?
(b) What is unreasonable about this velocity?
(c) Which premise or assumption is responsible?
Solution
(a) 7.03×108m/s size 12{ size 11{7 "." "03" times "10" rSup { size 8{8} } `"m/s"}} {}
(b) The velocity is too high—it’s greater than the speed of light
(c) The assumption that hydrogen inside a supernova behaves as an idea gas is responsible, because of the great temperature and density in the core of a star. Furthermore, when a velocity greater than the speed of light is obtained, classical physics must be replaced by relativity, a subject not yet covered.
94. Unreasonable Results
Suppose the relative humidity is 80% on a day when the temperature is 30.0ºC.
(a) What will the relative humidity be if the air cools to 25.0ºC and the vapor density remains constant?
(b) What is unreasonable about this result?
(c) Which premise is responsible?
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).

