10.6: Deformation of Solids

Last updated
Save as PDF

Page ID: 14499

Boundless
Boundless

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

Learning objectives

Explain how length of an object is determined

Length

In geometric measurements, length is the longest dimension of an object. In other contexts “length” is the measured dimension of an object. For example: it is possible to cut a length of a wire which is shorter than wire thickness. Length may be distinguished from height, which is vertical extent, and width or breadth, which are the distance from side to side, measuring across the object at right angles to the length.

Length is a measure of one dimension, whereas area is a measure of two dimensions (length squared) and volume is a measure of three dimensions (length cubed). In most systems of measurement, the unit of length is a fundamental unit, from which other units are defined.

After Albert Einstein’s Special Relativity Theory, length can no longer be thought of being constant in all reference frames. Thus, a ruler that is one meter long in one frame of reference will not be one meter long in a reference frame that is travelling at a velocity relative to the first frame. This means that the length of an object is variable depending on the observer.

Units

One of the oldest units of length measurement used in the ancient world was the ‘cubit,’ which was the length of the arm from the tip of the finger to the elbow. This could then be subdivided into shorter units like the foot, hand (which at 4 inches is still used today for expressing the height of horses) or finger, or added together to make longer units like the stride. The cubit could vary considerably due to the different sizes of people.

In the physical sciences and engineering, when one speaks of “units of length”, the word “length” is synonymous with “distance”. There are several units that are used to measure length. Units of length may be based on lengths of human body parts, the distance traveled in a number of paces, the distance between landmarks or places on the Earth, or arbitrarily on the length of some fixed object.In the International System of Units (SI), the basic unit of length is the meter and is now defined in terms of the speed of light. The centimeter and the kilometer, derived from the meter, are also commonly used units. In U.S. customary units, English or Imperial system of units, commonly used units of length are the inch, the foot, the yard, and the mile. Units used to denote distances in the vastness of space, as in astronomy, are much longer than those typically used on Earth and include the astronomical unit, the light-year, and the parsec.

Length: The metric length of one kilometre is equivalent to the imperial measurement of 0.62137 miles.

Shape

The shape of an object is a description of space that the object takes up; the shape can change if the object is deformed.

learning objectives

Describe effects of deformations, rotations, and magnifications

Shape

The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as color, content, and material composition

Simple and Complex Shapes

Simple shapes can be described by basic geometry objects such as a set of two or more points, a line, a curve, a plane, a plane figure (e.g. square or circle), or a solid figure (e.g. cube or sphere). Most shapes occurring in the physical world are complex. Some, such as plant structures and coastlines, may be so arbitrary as to defy traditional mathematical description – in which case they may be analyzed by differential geometry, or as fractals.

In geometry, two subsets of a Euclidean space have the same shape if one can be transformed to the other by a combination of translations, rotations (together also called rigid transformations), and uniform scalings. In other words, the shape of a set of points is all the geometrical information that is invariant to translations, rotations, and size changes. Having the same shape is an equivalence relation, and accordingly a precise mathematical definition of the notion of shape can be given as being an equivalence class of subsets of a Euclidean space having the same shape.

Shapes of physical objects are equal if the subsets of space these objects occupy satisfy the definition above. In particular, the shape does not depend on the size and placement in space of the object.

Shapes: Examples of shapes.

Volume

Volume is a measure of the three-dimensional space an object occupies, usually taken in terms of length, width and height.

learning objectives

Explain how is volume measured geometrically

Volume is the quantity of three-dimensional space contained by a closed boundary; it is the space that a substance (solid, liquid, gas or plasma) or shape occupies or contains. Volume is often quantified numerically using an SI derived unit, the cubic meter. However, for liquids the unit of volume used is known as the liter (equivalent to 0.001 cubic meters).

Measuring Volume: A measuring cup can be used to measure volumes of liquids. This cup measures volume in units of cups, fluid ounces and millilitres.

Volume is measured geometrically by multiplying an object’s three dimensions—usually taken as length, width and height. Some common volumes are taken as follows:

The volume of a cube: length times width times height.
The volume of a cylinder: the cross-sectional area times the height of the cylinder.
The volume of a sphere: 4/3 times the radius cubed times pi.

The volume of a solid can be determined by the volume of liquid it displaces when submerged.

The volume of a container is generally understood as the capacity of the container, meaning the amount of fluid (gas or liquid) the container can hold, rather than the amount of space the container itself displaces. Measuring cups, as seen in, work by taking a known cross sectional area of a cup and multiplying that by a variable height. Since liquid will always cover the cross section (if there is enough liquid), adding more liquid will increase the height inside the container.

Liquids take the shape of their container, filling up the minimum height needed. Gases, on the other hand, take up the maximum amount of volume possible. Thus a measuring cup can accurately measure the volume of a liquid, whereas a gas will always fill the entire container, more or less uniformly, no matter how little gas there is.

Stress and Strain

A point charge creates an electric field that can be calculated using Coulomb’s Law.

The electric field of a point charge is, like any electric field, a vector field that represents the effect that the point charge has on other charges around it. The effect is felt as a force and when charged particles are not in motion this force is known as the electrostatic force. The electrostatic force is, much like gravity, a force that acts at a distance. Therefore, we rationalize this action at a distance by saying that charges create fields around them that have effects on other charges.

Given a point charge, or a particle of infinitesimal size that contains a certain charge, electric field lines emanate radially in all directions. If the charge is positive, field lines point radially away from it; if the charge is negative, field lines point radially towards it.

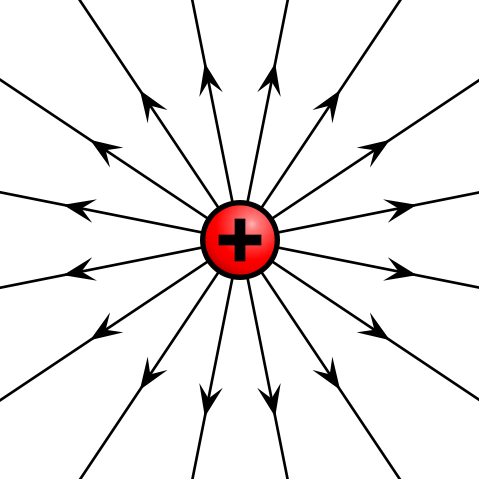
Electric field of positive point charge: The electric field of a positively charged particle points radially away from the charge.

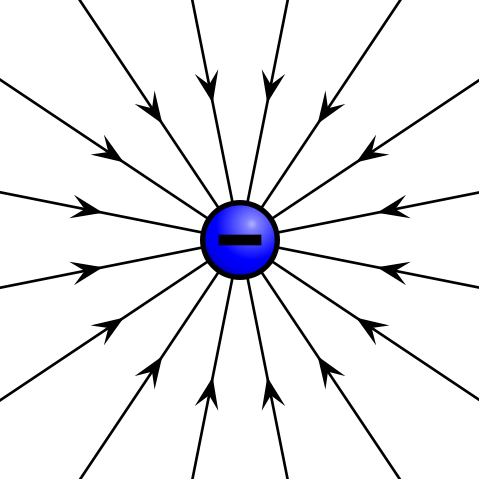
Electric field of negative point charge: The electric field of a negatively charged particle points radially toward the particle.

The reason for these directions can be seen in the derivation of the electric field of a point charge. Let’s first take a look at the definition of electric field of a point particle:

\[\mathrm{\overrightarrow{E}=\dfrac{1}{4πϵ_o}\dfrac{q}{r^2} \hat{r}=k\dfrac{q}{r^2} \hat{r}.}\]

In the above equation, q represents the charge of the particle creating the electric field and the constant k is a result of simply lumping the constants together. This charge is either positive or negative. If the charge is positive, as shown above, the electric field will be pointing in a positive radial direction from the charge q (away from the charge) and the following text explains why. The above equation is defined in radial coordinates which can be seen in.

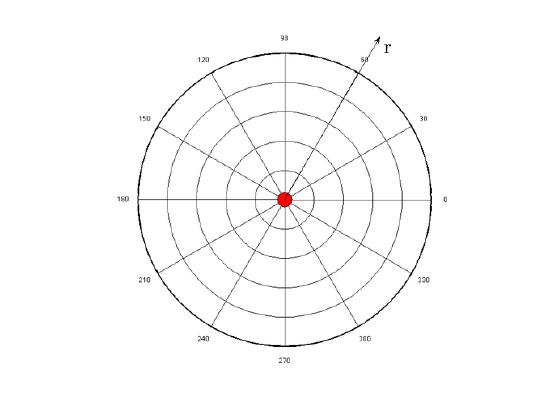
Radial Coordinate System: The electric field of a point charge is defined in radial coordinates. The positive r direction points away from the origin, and the negative r direction points toward the origin. The electric field of a point charge is symmetric with respect to the θ direction.

If we now place another positive charge, Q (called the test charge), at some radial distance, R, away from the original particle, the test charge will feel a force given by

\[\mathrm{\overrightarrow{F}=Q\overrightarrow{E}=Q\dfrac{1}{4πϵ_o}\dfrac{q}{R^2}\hat{r}}\]

The thing to keep in mind is that the force above is acting on the test charge Q, in the positive radial direction as defined by the original charge q. This means that because the charges are both positive and will repel one another, the force on the test charge points away from the original charge.

If the test charge were negative, the force felt on that charge would be

\[\mathrm{\overrightarrow{F}=Q\overrightarrow{E}=-Q\dfrac{1}{4πϵ_o}\dfrac{q}{R^2}\hat{r}}\]

Notice that this points in the negative \(\mathrm{\hat{r}}\) direction, which is toward the original charge. This makes sense because opposite charges attract and the force on the test charge will tend to push it toward the original positive charge creating the field. The above mathematical description of the electric field of a point charge is known as Coulomb ‘s Law.

Key Points

Length is typically a measure of the longest dimension of an object.
The deformation of an object is typically a change in length.
The SI unit of length is the meter.
The shape of an object is a representation of the space taken up by the object.
Deformations can change the shape of an object.
Objects that have the same shape can be transformed into each other by rotation or magnification.
Volume is often quantified numerically using an SI derived unit, the cubic meter. However, for liquids the unit of volume used is known as the liter (equivalent to 0.001 cubic meters).
This can also be understood as the amount of fluid a submerged object displaces.
Volume can be measured for geometrically regular objects by simple formulas. However, more complicated objects are easier to measure with fluid displacement.
The electric field is a vector field around a charged particle that represents the force that other charged particles would feel when placed near the particle creating the electric field.
Given a point charge, or a particle of infinitesimal size, that contains a certain charge, electric field lines emanate from equally in all radial directions.
If the point charge is positive, field lines point away from it; if the charge is negative, field lines point towards it.

Key Terms

dimension: A measure of spatial extent in a particular direction, such as height, width or breadth, or depth.
special relativity: A theory that (neglecting the effects of gravity) reconciles the principle of relativity with the observation that the speed of light is constant in all frames of reference.
plane: A level or flat surface.
Euclidean: Adhering to the principles of traditional geometry, in which parallel lines are equidistant.
cross section: A section formed by a plane cutting through an object, usually at right angles to an axis.
dimension: A measure of spatial extent in a particular direction, such as height, width or breadth, or depth.
coulomb’s law: the mathematical equation calculating the electrostatic force vector between two charged particles
vector field: a construction in which each point in a Euclidean space is associated with a vector; a function whose range is a vector space

Search

Text Color

Text Size

Margin Size

Font Type