21.3: Radioactivity

Radioactive decay is the emission of some particle from an atomic nucleus, accompanied by a change of state or type of the nucleus, depending on the type of radioactivity.

Gamma rays or photons are emitted when a nucleus decays from an excited state to its ground state. No transformation of the nuclear type occurs. Photons are often emitted when some other form of radioactive decay leaves the resulting nucleus in an excited state.

Figure 21.5: Approximate curve for the energy released in alpha decay of a nucleus on the line of stability. Decay is only possible if \(Q > 0\).

Beta minus decay is the conversion of a neutron into a proton, an electron, and an electron antineutrino. This and the inverse reaction, beta plus decay, or conversion of a proton into a neutron, a positron, and an electron neutrino, were described in chapter 18. These processes occur in the nucleons contained in nuclei when they are energetically possible.

Alpha particle emission occurs in heavy elements where it is energetically possible. Since an alpha particle is just a helium 4 nucleus containing two protons and two neutrons, the values of \(Z\) and \(N\) of the emitting nucleus are each reduced by two.

The rest energy of a nucleus (ignoring atomic effects) is just the sum of the rest energies of all the nucleons minus the total binding energy for the nucleus:

\[M(Z, A) c^{2}=Z M_{p} c^{2}+N M_{n} c^{2}-B(Z, A)\label{21.3}\]

where \(M_{p} c^{2}=938.280 \mathrm{MeV}\) is the rest energy of the proton and \(\mathrm{M}_{\mathrm{n}} \mathrm{c}^{2}=939.573 \mathrm{MeV}\) is the rest energy of the neutron.

Energy conservation requires that

\[M(Z, A) c^{2}=M(Z-2, A-4) c^{2}+M(2,4) c^{2}+Q\label{21.4}\]

for the alpha decay of a nucleus. If \(Q > 0\), then the decay is energetically possible. The excess energy, \(Q\), goes into kinetic energy of the new nucleus and the alpha particle, mainly the latter. Substitution of equation (\ref{21.3}) into equation (\ref{21.4}) yields

\[Q=B(Z-2, A-4)+B(2,4)-B(Z, A) \quad(\text { alpha decay })\label{21.5}\]

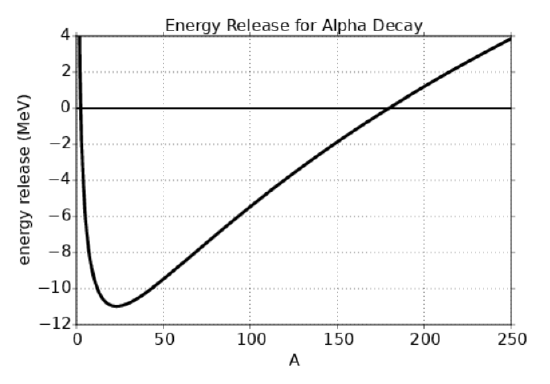
The binding energy of the alpha particle is not accurately represented by equation (21.2.1), but is known to be about \(B(2,4)=28.3 \mathrm{MeV}\). On the other hand, the heavy elements are generally well represented by equation (21.2.1). The curve of \(Q\) versus A is plotted in figure 21.5, and it shows that alpha decay for nuclei along the line of stability is energetically impossible (i. e., Q < 0) for nuclei with A less than about 175.

Figure 21.6: Schematic illustration of the paths of nuclear transformations in the N-Z plane due to alpha and beta decay. The thick line represents the line of stability. \(\beta^{+}\) is the decay of a proton into a neutron, positron, and electron neutrino, while \(\beta^{-}\) is the decay of a neutron into a proton, electron, and electron antineutrino.

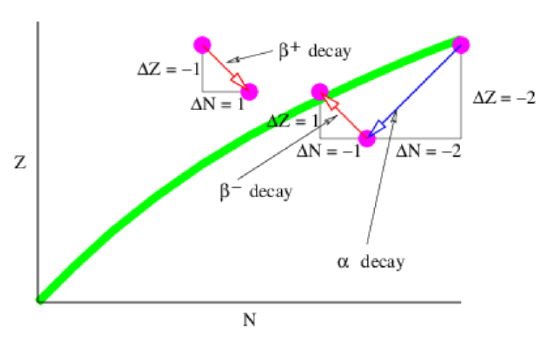
Figure 21.6 shows schematically how alpha and beta decay transform atomic nuclei in the \(N-Z\) plane. As previously indicated, alpha decay decreases both \(Z\) and \(N\) by two. Ordinary beta decay (i. e., \(n \rightarrow p^{+}+e^{-}+v_{e}\)) decreases \(N\) by one and increases \(Z\) by one. This is sometimes called β^- decay since it produces an electron with negative charge. Though the proton in isolation is stable, the energetics of atomic nuclei are such that a nucleus with a higher proton-neutron ratio than specified by the line of stability can sometimes release energy by the reaction \(\mathrm{p}^{+} \rightarrow \mathrm{n}+\mathrm{e}^{+}+\mathrm{v}_{\mathrm{e}}\). This is called \(\beta^{+}\) decay since it produces a positively charged positron.

Certain isotopes of very heavy elements are at the head of a chain of radioactive decays. This chain consists of a combination of alpha decays interspersed with \(\beta^{-}\) decays. The latter are needed because the alpha decays create nuclei with too low a ratio of protons to neutrons relative to the line of stability, as illustrated in figure 21.6. The beta decays push the chain back toward this line. An example of a chain is one that starts with the element thorium \((Z = 90, A = 232)\) and ends with lead (Z = 82, A = 208). Radioactive decay thus accomplishes what medieval alchemists tried, but failed, to do: transmute elements from one type into another. Unfortunately, no radioactive chain ends at the element gold!

Radioactive decay is governed by a simple law, namely that the rate at which nuclei decay is proportional to the number of remaining nuclei. In mathematical terms, this is expressed as follows:

\[\frac{d N}{d t}=-\lambda N\label{21.6}\]

where \(N(t)\) is the number of remaining nuclei at time \(t\) and \(\lambda\) is called the decay rate. This differential equation has the solution

\[N(t)=N(0) \exp (-\lambda t) \quad \text { (radioactive decay) }\label{21.7}\]

which shows that the number of nuclei decreases exponentially with time.

The half-life, \(\mathrm{t}_{1 / 2}\) of a certain nuclear type, is the time required for half the nuclei to decay. Setting \(N\left(t_{1 / 2}\right)=N(0) / 2\), we find that

\[t_{1 / 2}=\frac{\ln (2)}{\lambda} \quad \text { (half-life). }\label{21.8}\]

The nature of exponential decay means that half the particles are left after one half-life, a quarter after two half-lives, an eighth after three half-lives, etc. The actual value of \(\lambda\), and hence \(\mathrm{t}_{1 / 2}\), depends on the character of the nucleus in question, with half-lives ranging from a small fraction of a second to many billions of years.