21.2: Nuclear Binding Energies
- Page ID
- 32882
It is impossible to specify an accurate inter-nucleon force valid under all circumstances, but figure 21.1 gives an approximate representation of the potential energy associated with the strong force as the function of nucleon separation. The binding energy is of order 2 MeV, with an attractive force for separations greater than about \(2 \times 10^{-15}\) m and an intense repulsive force for smaller separations. At large distances the potential energy decays exponentially with distance rather than according to the \(r^{-1}\) law of the Coulomb potential.
The short range of the inter-nuclear force means that atomic nuclei can be thought of as conglomerations of “sticky billiard balls”. The nuclear force is essentially a contact force and each nucleon simply binds to all its nearest neighbors. When nucleons are close-packed, the binding energy per nucleon due to the strong force is simply the number of nearest neighbors for each nucleon, multiplied by the binding energy per nucleon pair, divided by 2. The factor of \(1 / 2\) accounts for the fact that each nuclear bond is shared by two nucleons.
Several other effects need to be accounted for in the nucleus. The nucleons on the surface of the nucleus do not have as many bonds as nucleons in the interior. Thus, to compute the nuclear binding energy of a nucleus with a finite number of nucleons, a correction must be made for this effect. This contributes negatively to the nuclear binding energy in proportion to the surface area of the nucleus, which scales as the number of nucleons to the two-thirds power.
In addition to the nuclear force, the repulsive electrostatic force between protons needs to be accounted for. Since the electrostatic force is a long range force, the (negative) contribution to the binding energy of the nucleus goes as the square of the number of protons divided by the radius of the nucleus. The latter goes as the cube root of the number of nucleons.
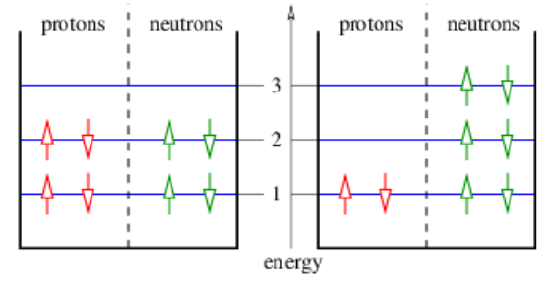
The Pauli exclusion principle operates in nuclei so as to favor equal numbers of protons and neutrons. This effect is illustrated in figure 21.2. If a proton is converted into a neutron in a nucleus in which equal numbers of the two particles occur, then the exclusion principle forces these nucleons to move to a higher energy level than they previously occupied. The binding energy of the nucleus is correspondingly decreased. This effect opposes the weaker, repulsive Coulomb potential that occurs when there are more neutrons and fewer protons.
The net result of all these effects is a nuclear binding energy equation with four terms representing the four above-mentioned effects:
\[B(Z, A)=a_{v} A-a_{s} A^{2 / 3}-a_{c} Z^{2} / A^{1 / 3}-a_{a}(2 Z-A)^{2} / A\label{21.1}\]
where Z is the atomic number or the number of protons, N is the number of neutrons, and \(A = Z + N\) is the atomic mass number, or number of nucleons. Equation (\ref{21.1}) represents the binding energy of the entire nucleus. The binding energy per nucleon is just \(\mathrm{B} / \mathrm{A}\).
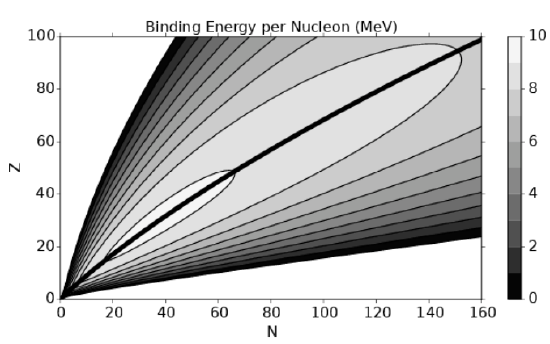
Fitting Equation \ref{21.1} to observed binding energies in nuclei yields the following values for the coefficients of the above equation: \(a_{v} \approx 16 \mathrm{MeV}\), \(a_{s} \approx 17 \mathrm{MeV}\), \(a_{c} \approx 0.70 \mathrm{MeV}\), and \(a_{a} \approx 23 \mathrm{MeV}\). A contour plot of binding energy per nucleon, \(B ∕ A\), is shown in figure 21.3. We note that this equation doesn’t work well for nuclei with only a few nucleons. For instance, the helium nucleus with \(A = 4\) is more stable than the lithium nucleus with \(A = 6\), and there is no stable nucleus at all with \(A = 5\).
Part of the reason for the problem at small A is that even numbers of protons and neutrons tend to bind more strongly together than nuclei containing odd numbers of either. This is because pairs of protons or neutrons with opposite spins fully occupy nuclear states while an odd nucleon occupies a state by itself with energy greater than that of all the other occupied states. This behavior can be approximately accounted for by adding the term \(a_{p} / A^{1 / 2}\) to equation (\ref{21.1}), where \(a_{p}=12 \mathrm{MeV}\) if \(N\) and \(Z\) are both even, \(a_{p}=0\) if either \(N\) or \(Z\) is odd, and \(a_{p}=-12 \mathrm{MeV}\) if both are odd. We leave this term off even though it is sometimes quite important, in order to make equation (\ref{21.1}) a smooth function of \(Z\) and \(A\) and thus representative of the general trend of binding energy.
For a given value of A, it is easy to demonstrate that the maximum nuclear binding energy in equation (\ref{21.1}) occurs when
\[Z=\frac{A}{2\left(1+a_{c} A^{2 / 3} / 4 a_{a}\right)}\label{21.2}\]
This formula confirms the trend seen in figure 21.3 that the most stable nuclear configuration contains an increasing fraction of neutrons as A increases. The function \(Z(N)\) given by equation (\ref{21.2}) and illustrated by the curve starting near the origin in figure 21.3 defines the line of stability for atomic nuclei.
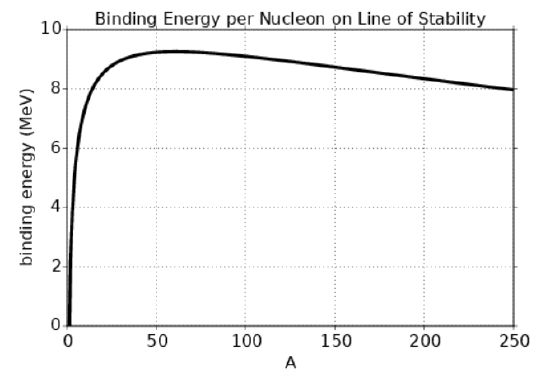
Figure 21.4 shows the binding energy per nucleon as a function of nucleon number \(A\) along the line of stability. The rapid increase in binding energy for small A reflects the decreasing surface effect as the number of nucleons increases. The subsequent decrease is a result of the combined effects of Coulomb repulsion of protons and the Pauli exclusion principle. Notice that the maximum binding energy per nucleon occurs near \(A = 60\).
The chemical properties of the atom associated with an atomic nucleus are determined by the number of protons, \(Z\), in the nucleus. In many cases there exists more than one stable or long-lived nucleus with a given value of \(Z\). These nuclei differ in their neutron number, \(N\). Nuclei with the same \(Z\) and differing \(N\) are called isotopes of the element defined by the specified value of \(Z\). For instance, there are three isotopes of the element hydrogen, normal hydrogen, deuterium, and tritium, with zero, one, and two neutrons respectively.
