1.2: Sine Waves

Figure \(\PageIndex{1}\): .2: Definition sketch for a sine wave, showing the wavelength \(\lambda\) and the amplitude \(h_{0}\) and the phase \(\phi\) at various points.

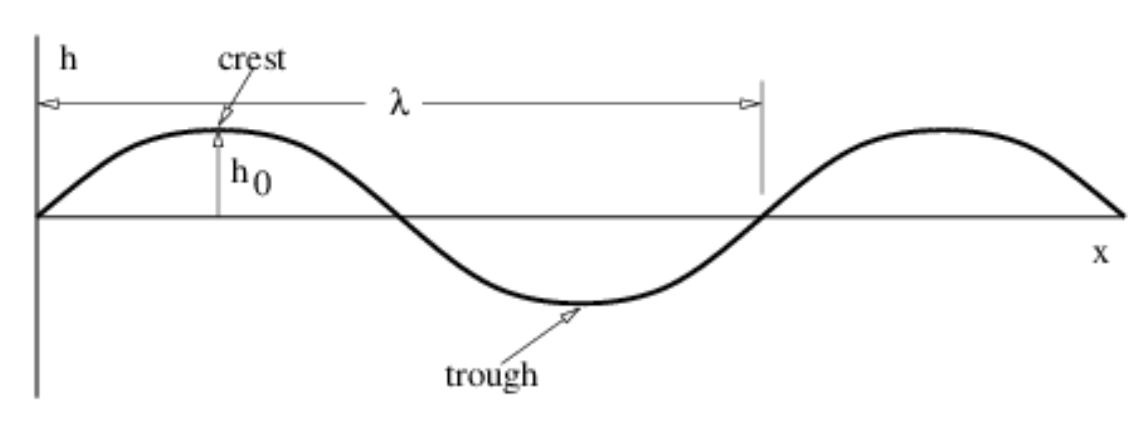
A particularly simple kind of wave, the sine wave, is illustrated in figure 1.2. This has the mathematical form

\[h(x)=h_{0} \sin (2 \pi x / \lambda)\label{1.1}\]

where h is the displacement (which can be either longitudinal or transverse), h₀ is the maximum displacement, also called the amplitude of the wave, and λ is the wavelength. The oscillatory behavior of the wave is assumed to carry on to infinity in both positive and negative x directions. Notice that the wavelength is the distance through which the sine function completes one full cycle. The crest and the trough of a wave are the locations of the maximum and minimum displacements, as seen in figure 1.2.

So far we have only considered a sine wave as it appears at a particular time. All interesting waves move with time. The movement of a sine wave to the right a distance d may be accounted for by replacing x in the above formula by \(x - d\). If this movement occurs in time \(t\), then the wave moves at velocity \(c = d∕t\). Solving this for d and substituting yields a formula for the displacement of a sine wave as a function of both distance \(x\) and time \(t\):

\[h(x, t)=h_{0} \sin [2 \pi(x-c t) / \lambda\label{1.2}\]

The time for a wave to move one wavelength is called the period of the wave: \(T=\lambda / c\). Thus, we can also write

\[h(x, t)=h_{0} \sin [2 \pi(x / \lambda-t / T)]\label{1.3}\]

Physicists actually like to write the equation for a sine wave in a slightly simpler form. Defining the wavenumber as \(k=2 \pi \lambda\) and the angular frequency as \(\omega=2 \pi T\), we write

\[h(x, t)=h_{0} \sin (k x-\omega t)\label{1.4}\]

We normally think of the frequency of oscillatory motion as the number of cycles completed per second. This is called the rotational frequency, and is given by \(f=1 / T\). It is related to the angular frequency by \(\omega=2 \pi f\). The rotational frequency is usually easier to measure than the angular frequency, but the angular frequency tends to be used more often in theoretical discussions. As shown above, converting between the two is not difficult. Rotational frequency is measured in units of hertz, abbreviated Hz; \(1 \mathrm{~Hz}=1 \text { cycle } \mathrm{s}^{-1}\). Angular frequency also has the dimensions of inverse time, e. g., radian s^-1, but the term “hertz” is generally reserved only for rotational frequency.

The argument of the sine function is by definition an angle. We refer to this angle as the phase of the wave, \(\phi=k x-\omega t\). The difference in the phase of a wave at fixed time over a distance of one wavelength is \(2 \pi\), as is the difference in phase at fixed position over a time interval of one wave period.

Since angles are dimensionless, we normally don’t include this in the units for frequency. However, it sometimes clarifies things to refer to the dimensions of rotational frequency as “rotations per second” or angular frequency as “radians per second”.

As previously noted, we call \(h_{0}\), the maximum displacement of the wave, the amplitude. Often we are interested in the intensity of a wave, which is proportional to the square of the amplitude. The intensity is often related to the amount of energy being carried by a wave.

The wave speed we have defined above, \(c=\lambda/T\), is actually called the phase speed. Since \(\lambda=2 \pi k \text { and } T=2 \pi / \omega\), we can write the phase speed in terms of the angular frequency and the wavenumber:

\[c=\frac{\omega}{k} \quad(\text { phase speed })\label{1.5}\]