1.4: Superposition Principle

It is found empirically that as long as the amplitudes of waves in most media are small, two waves in the same physical location don’t interact with each other. Thus, for example, two waves moving in the opposite direction simply pass through each other without their shapes or amplitudes being changed. When collocated, the total wave displacement is just the sum of the displacements of the individual waves. This is called the superposition principle. At sufficiently large amplitude the superposition principle often breaks down — interacting waves may scatter off of each other, lose amplitude, or change their form.

Interference is a consequence of the superposition principle. When two or more waves are superimposed, the net wave displacement is just the algebraic sum of the displacements of the individual waves. Since these displacements can be positive or negative, the net displacement can either be greater or less than the individual wave displacements. The former case, which occurs when both displacements are of the same sign, is called constructive interference, while destructive interference occurs when they are of opposite sign.

Figure \(\PageIndex{1}\): .5: Superposition (lower panel) of two sine waves (shown individually in the upper panel) with equal amplitudes and wavenumbers \(k_{1}=4 \text { and } k_{2}=5\).

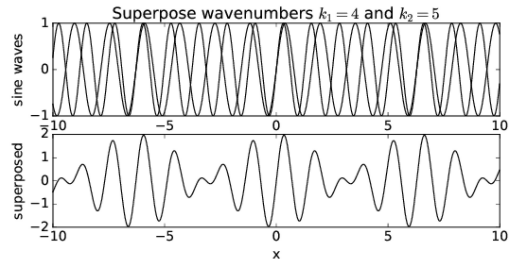
Let us see what happens when we superimpose two sine waves with different wavenumbers. Figure 1.5 shows the superposition of two waves with wavenumbers k₁ = 4 and k₂ = 5. Notice that the result is a wave with about the same wavelength as the two initial waves, but which varies in amplitude depending on whether the two sine waves are interfering constructively or destructively. We say that the waves are in phase if they are interfering constructively, and they are out of phase if they are interfering destructively.

Figure \(\PageIndex{1}\): .6: Superposition of two sine waves with equal amplitudes and wavenumbers k₁ = 10 and k₂ = 11.

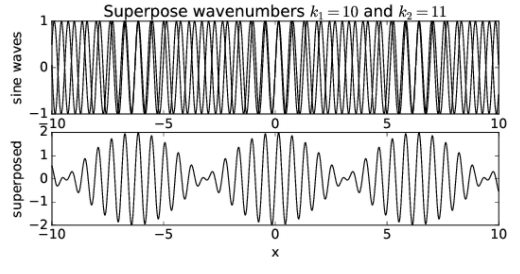
What happens when the wavenumbers of the two sine waves are changed? Figure 1.6 shows the result when k₁ = 10 and k₂ = 11. Notice that though the wavelength of the resultant wave is decreased, the locations where the amplitude is maximum have the same separation in x as in figure 1.5.

Figure \(\PageIndex{1}\): .7: Superposition of two sine waves with equal amplitudes and wavenumbers k₁ = 10 and k₂ = 12.

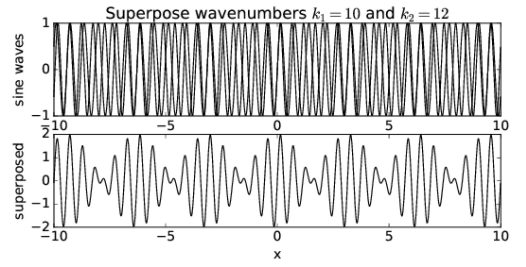
If we superimpose waves with k₁ = 10 and k₂ = 12, as is shown in figure 1.7, we see that the x spacing of the regions of maximum amplitude has decreased by a factor of two. Thus, while the wavenumber of the resultant wave seems to be related to something like the average of the wavenumbers of the component waves, the spacing between regions of maximum wave amplitude appears to go inversely with the difference of the wavenumbers of the component waves. In other words, if k₁ and k₂ are close together, the amplitude maxima are far apart and vice versa.

Figure \(\PageIndex{1}\): .8: Representation of the wavenumbers and amplitudes of two superimposed sine waves.

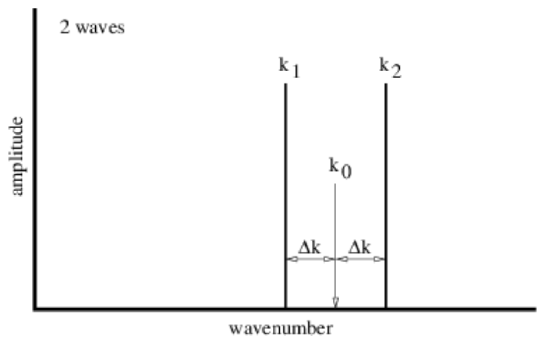
We can symbolically represent the sine waves that make up figures 1.5, 1.6, and 1.7 by a plot such as that shown in figure 1.8. The amplitudes and wavenumbers of each of the sine waves are indicated by vertical lines in this figure.

Figure \(\PageIndex{1}\): .9: Superposition of twenty sine waves with k₀ = 4 and Δk = 1.

Figure \(\PageIndex{1}\): .10: Representation of the distribution of wavenumbers and amplitudes of 20 superimposed sine waves with maximum at k₀ = 4 and half-width Δk = 1.

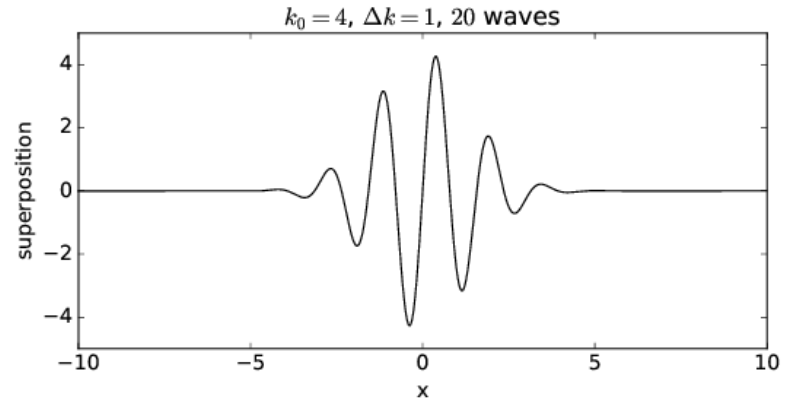
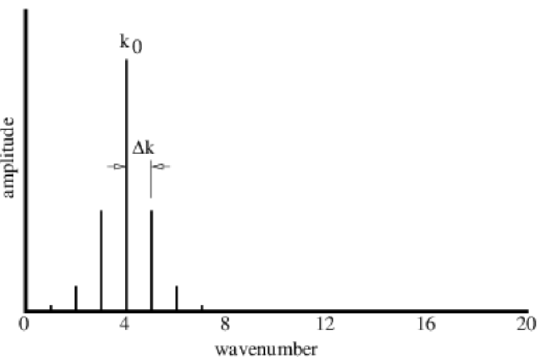
The regions of large wave amplitude are called wave packets. Wave packets will play a central role in what is to follow, so it is important that we acquire a good understanding of them. The wave packets produced by only two sine waves are not well separated along the x-axis. However, if we superimpose many waves, we can produce an isolated wave packet. For example, figure 1.9 shows the results of superimposing 20 sine waves with wavenumbers \(k=0.4 m, m=1,2, \ldots, 20\), where the amplitudes of the waves are largest for wavenumbers near \(k = 4\). In particular, we assume that the amplitude of each sine wave is proportional to \(\exp \left[-\left(k-k_{0}\right)^{2} / \Delta k^{2}\right]\), where k ₀ = 4 defines the maximum of the distribution of wavenumbers and \(Δk = 1\) defines the half-width of this distribution. The amplitudes of each of the sine waves making up the wave packet in figure 1.9 are shown schematically in figure 1.10.

Figure \(\PageIndex{1}\): .11: Superposition of twenty sine waves with k₀ = 4 and Δk = 2.

Figure \(\PageIndex{1}\): .12: Representation of the distribution of wavenumbers and amplitudes of 20 superimposed sine waves with maximum at k₀ = 4 and half-width Δk = 2.

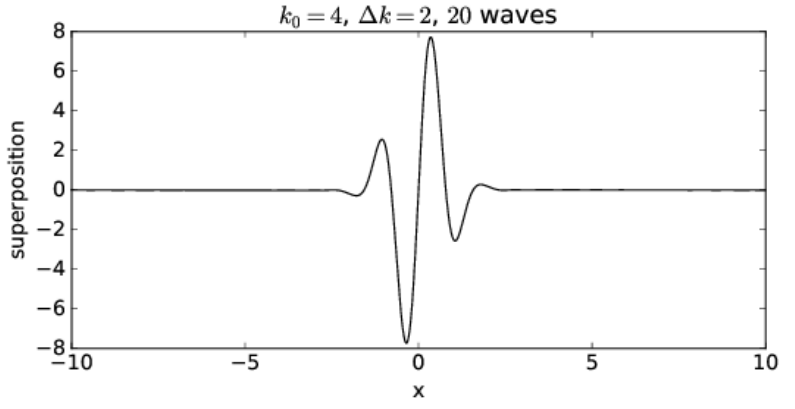
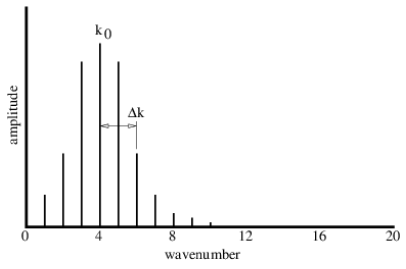
The quantity \(Δk\) controls the distribution of the sine waves being superimposed — only those waves with a wavenumber k within approximately Δk of the central wavenumber k₀ of the wave packet, i. e., for \(3 ≤ k ≤ 5\) in this case, contribute significantly to the sum. If \(Δk\) is changed to 2, so that wavenumbers in the range 2 ≤ k ≤ 6 contribute significantly, the wavepacket becomes narrower, as is shown in figures 1.11 and 1.12. \(Δk\) is called the wavenumber spread of the wave packet, and it evidently plays a role similar to the difference in wavenumbers in the superposition of two sine waves — the larger the wavenumber spread, the smaller the physical size of the wave packet. Furthermore, the wavenumber of the oscillations within the wave packet is given approximately by the central wavenumber.

We can better understand how wave packets work by mathematically analyzing the simple case of the superposition of two sine waves. Let us define k₀ = (k₁ + k₂)∕2 where k₁ and k₂ are the wavenumbers of the component waves. Furthermore let us set Δk = (k₂ - k₁) ∕ 2. The quantities k₀ and Δk are graphically illustrated in figure 1.8. We can write \(k_{1}=k_{0}-\Delta k \text { and } k_{2}=k_{0}+\Delta k\) and use the trigonometric identity \(sin(a + b) = sin(a) cos(b) + cos(a) sin(b)\) to find

\[\begin{equation}
\begin{aligned}
\sin \left(k_{1} x\right)+\sin \left(k_{2} x\right)=& \sin \left[\left(k_{0}-\Delta k\right) x\right]+\sin \left[\left(k_{0}+\Delta k\right) x\right] \\
=& \sin \left(k_{0} x\right) \cos (\Delta k x)-\cos \left(k_{0} x\right) \sin (\Delta k x)+\\
& \sin \left(k_{0} x\right) \cos (\Delta k x)+\cos \left(k_{0} x\right) \sin (\Delta k x) \\
=& 2 \sin \left(k_{0} x\right) \cos (\Delta k x)
\end{aligned}
\end{equation}\label{1.17}\]

The sine factor on the bottom line of the above equation produces the oscillations within the wave packet, and as speculated earlier, this oscillation has a wavenumber k₀ equal to the average of the wavenumbers of the component waves. The cosine factor modulates this wave with a spacing between regions of maximum amplitude of

\[\Delta x=\pi / \Delta k\label{1.18}\]

Thus, as we observed in the earlier examples, the length of the wave packet Δx is inversely related to the spread of the wavenumbers Δk (which in this case is just the difference between the two wavenumbers) of the component waves. This relationship is central to the uncertainty principle of quantum mechanics.