1.3: Types of Waves

In order to make the above material more concrete, we now examine the characteristics of various types of waves which may be observed in the real world.

Ocean Surface Waves

Figure \(\PageIndex{1}\): .3: Wave on an ocean of depth H. The wave is moving to the right and the particles of water at the surface oscillate in elliptical trajectories as the wave crests and troughs pass.

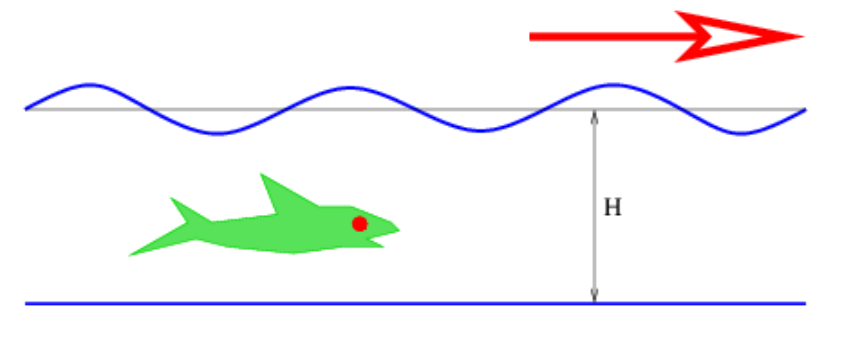
These waves are manifested as undulations of the ocean surface as seen in Figure \(\PageIndex{3}\):. The speed of ocean waves is given by the formula

\[c=\left(\frac{g \tanh (k H)}{k}\right)^{1 / 2}\label{1.6}\]

where g = 9.8 m s^-2 is the earth’s gravitational force per unit mass, H is the depth of the ocean, and the hyperbolic tangent is defined as¹

\[\tanh (x)=\frac{\exp (x)-\exp (-x)}{\exp (x)+\exp (-x)}\label{1.7}\]

The equation for the speed of ocean waves comes from the theory for oscillations of a fluid surface in a gravitional field.

Figure \(\PageIndex{1}\): .4: Plot of the function \(\tanh (x)\). The dashed line shows our approximation \(\tanh (x) \approx x \text { for }|x|<1\).

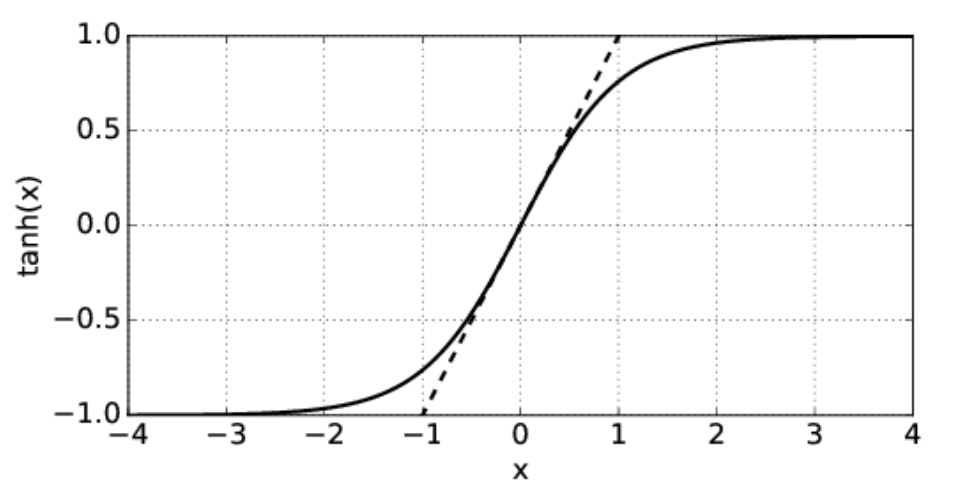
As figure 1.4 shows, for \(|x|≪ 1\), we can approximate the hyperbolic tangent by \(tanh(x) ≈ x\), while for \(|x|≫ 1\) it is +1 for \(x > 0\) and -1 for \(x < 0\). This leads to two limits: Since \(x = kH\), the shallow water limit, which occurs when \(kH ≪ 1\), yields a wave speed of

\[c \approx(g H)^{1 / 2}, \quad \text { (shallow water waves) }\label{1.8}\]

while the deep water limit, which occurs when \(kH ≫ 1\), yields

\[c \approx(g / k)^{1 / 2}, \quad \text { (deep water waves). }\label{1.9}\]

Notice that the speed of shallow water waves depends only on the depth of the water and on g. In other words, all shallow water waves move at the same speed. On the other hand, deep water waves of longer wavelength (and hence smaller wavenumber) move more rapidly than those with shorter wavelength. Waves for which the wave speed varies with wavelength are called dispersive. Thus, deep water waves are dispersive, while shallow water waves are non-dispersive.

For water waves with wavelengths of a few centimeters or less, surface tension becomes important to the dynamics of the waves. In the deep water case, the wave speed at short wavelengths is given by the formula

\[c=(g / k+A k)^{1 / 2}\label{1.10}\]

where the constant A is related to an effect called surface tension. For an air-water interface near room temperature, \(A \approx 74 \mathrm{~cm}^{3} \mathrm{~s}^{-2}\)

Sound Waves

Sound is a longitudinal compression-expansion wave in a fluid. The wave speed for sound in an ideal gas is

\[c=\left(\gamma R T_{a b s}\right)^{1 / 2}\label{1.11}\]

where \(γ \) and \(R \) are constants and \(T\) _abs is the absolute temperature . The absolute temperature is measured in Kelvins and is numerically given by

\[T_{a b s}=T_{C}+273^{\circ} \label{1.12}\]

where \(T\) _C is the temperature in Celsius degrees. The angular frequency of sound waves is thus given by

\[\omega=c k=\left(\gamma R T_{a b s}\right)^{1 / 2} k\label{1.13}\]

The speed of sound in air at normal temperatures is about 340 m s^-1.

Light

Light moves in a vacuum at a speed of \(c_{v a c}=3 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}\). In transparent materials it moves at a speed less than \(c_{v a c}\) by a factor \(n\) which is called the refractive index of the material:

\[c=c_{v a c} / n\label{1.14}\]

Often the refractive index takes the form

\[n^{2} \approx 1+\frac{A}{1-\left(k / k_{R}\right)^{2}}\label{1.15}\]

where \(k\) is the wavenumber and \(k_{R}\) and \(A\) are positive constants characteristic of the material. The angular frequency of light in a transparent medium is thus

\[\omega=k c=k c_{v a c} / n\label{1.16}\]