2.4: Diffraction Through a Single Slit

Last updated
Save as PDF

Page ID: 32928

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

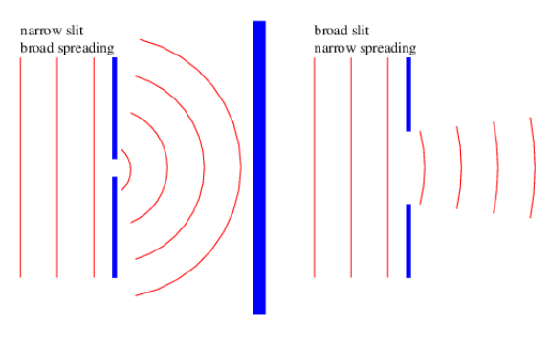
How does all of this apply to the passage of waves through a slit? Imagine a plane wave of wavelength λ impingent on a barrier with a slit. The barrier transforms the plane wave with infinite extent in the lateral direction into a beam with initial transverse dimensions equal to the width of the slit. The subsequent development of the beam is illustrated in figures 2.13 and 2.14, and schematically in figure 2.15. In particular, if the slit width is comparable to the wavelength, the beam spreads broadly as in figure 2.13. If the slit width is large compared to the wavelength, the beam doesn’t spread as much, as figure 2.14 illustrates. Equation (2.3.7) gives us an approximate quantitative result for the spreading angle if w is interpreted as the width of the slit.

Figure \(\PageIndex{2}\): .15: Schematic behavior when a plane wave impinges on a narrow slit and a broad slit.

One use of the above equation is in determining the maximum angular resolution of optical instruments such as telescopes. The primary lens or mirror can be thought of as a rather large “slit”. Light from a distant point source is essentially in the form of a plane wave when it arrives at the telescope. However, the light passed by the telescope is no longer a plane wave, but is a beam with a tendency to spread. The spreading angle α_max is given by equation (2.3.7), and the telescope cannot resolve objects with an angular separation less than α_max. Replacing w with the diameter of the lens or mirror in equation (2.3.7) thus yields the telescope’s angular resolution. For instance, a moderate sized telescope with aperture 1 m observing red light with λ ≈ 6 × 10^-7 m has a maximum angular resolution of about 3 × 10^-7 radians.