2.5: Two Slits

Last updated
Save as PDF

Page ID: 32929

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Let us now imagine a plane sine wave normally impingent on a screen with two narrow slits spaced by a distance d, as shown in figure 2.16. Since the slits are narrow relative to the wavelength of the wave impingent on them, the spreading angle of the beams is large and the diffraction pattern from each slit individually is a cylindrical wave spreading out in all directions, as illustrated in figure 2.13. The cylindrical waves from the two slits interfere, resulting in oscillations in wave intensity at the screen on the right side of figure 2.16.

Figure \(\PageIndex{2}\): .16: Definition sketch for the double slit. Light passing through slit B travels an extra distance to the screen equal to \(d\sin\theta\) compared to light passing through slit A.

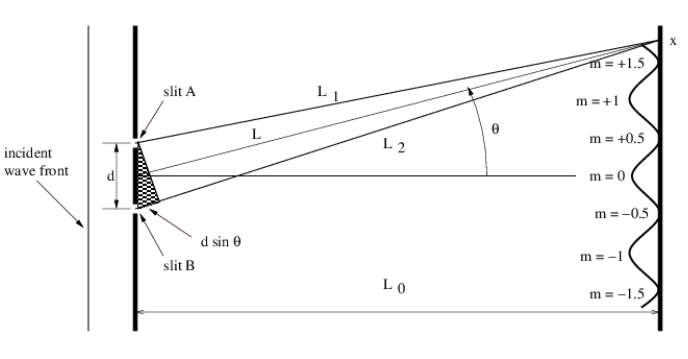
Constructive interference occurs when the difference in the paths traveled by the two waves from their originating slits to the screen, \(L_{2}-L_{1}\) is an integer multiple m of the wavelength \(\lambda: L_{2}-L_{1}=m \lambda . \text { If } L_{0} \gg d\) the lines \(L_{1}\) and \(L_{2}\) are nearly parallel, which means that the narrow end of the dark triangle in figure 2.16 has an opening angle of \(\theta\). Thus, the path difference between the beams from the two slits is \(L_{2}-L_{1}=d \sin \theta\). Substitution of this into the above equation shows that constructive interference occurs when

\[d \sin \theta=m \lambda, \quad m=0,\pm 1,\pm 2, \ldots \quad \text { (two slit interference). }\label{2.22}\]

Destructive interference occurs when m is an integer plus \(1/2\). The integer m is called the interference order and is the number of wavelengths by which the two paths differ.