3.6: Problems

Last updated
Save as PDF

Page ID: 32937

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The index of refraction varies as shown in figure 3.14:
1. Given θ₁, use Snell’s law to find θ₂.
2. Given θ₂, use Snell’s law to find θ₃.
3. From the above results, find θ₃, given θ₁. Do n₂ or θ₂ matter? 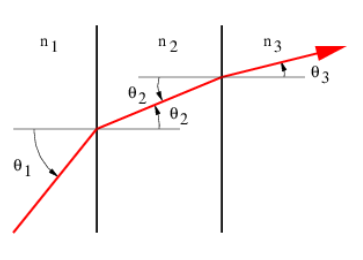Figure 3.14: Refraction through multiple parallel layers with different refractive indices.
A 45^∘-45^∘-90^∘ prism is used to totally reflect light through 90^∘ as shown in figure 3.15. What is the minimum index of refraction of the prism needed for this to work? 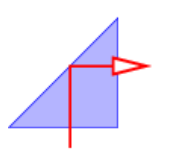Figure 3.15: Refraction through a 45^∘-45^∘-90^∘ prism.
Show graphically which way the wave vector must point inside the calcite crystal of figure 3.3 for a light ray to be horizontally oriented. Sketch the orientation of the wave fronts in this case. 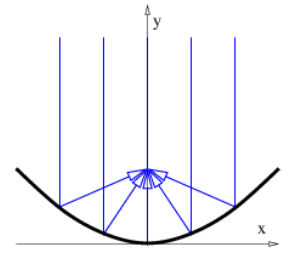Figure 3.16: Focusing of parallel rays by a parabolic mirror.
The human eye is a lens which focuses images on a screen called the retina. Suppose that the normal focal length of this lens is 4 cm and that this focuses images from far away objects on the retina. Let us assume that the eye is able to focus on nearby objects by changing the shape of the lens, and thus its focal length. (The lens-retina distance remains the same.) If an object is 20 cm from the eye, what must the altered focal length of the eye be in order for the image of this object to be in focus on the retina?
An amoeba 0.01 cm in diameter has its image projected on a screen as shown in figure 3.18 by a positive lens of diameter 0.1 cm.
1. How big is the image of the amoeba?
2. What is the focal length of the lens?
3. What is the minimum distance between features on the image of the amoeba which can be resolved? Assume that the wavelength of light used is 5 × 10^-7 m. (Hint: What is the spreading angle of a beam of light passing through an opening the size of the lens?) Figure 3.18: An amoeba imaged by a lens.
The great refractor telescope of Yerkes Observatory in Wisconsin (see figure 3.19) has primary lens D = 1.02 m in diameter with a focal length of L = 19.4 m. Use the small angle approximation in all calculations and assume that the light has wavelength 5 × 10^-7 m.
1. Jupiter has a diameter of 1.5 × 10⁵ km and an average distance from the earth of 8 × 10⁸ km. How big is the image of Jupiter (in cm) at the focal plane of the primary lens?
2. Given perfect atmospheric “seeing” conditions, how far apart must two features be on Jupiter (in km) for the Yerkes telescope to be able to resolve them.
3. What should the focal length l of the secondary lens or eyepiece be for Jupiter to subtend the same angle as the moon subtends to the naked eye? The moon’s diameter is 3.5 × 10³ km and its distance from the earth is 3.8 × 10⁵ km. Hint: Imagine that a translucent sheet of ground glass is placed at the focal plane so that the image is seen projected on this ground glass, which scatters light over a broad range of angles. The eyepiece can then be thought of as a magnifying glass with which you can examine the image on the ground glass. Using this artiface, you need consider only light rays that pass through the center of each lens. 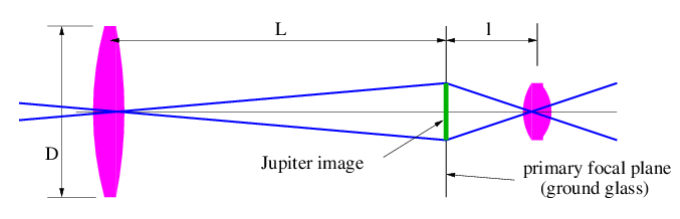Figure 3.19: The great Yerkes refractor telescope observing Jupiter.
Show that a concave mirror that focuses incoming rays parallel to the optical axis of the mirror to a point on the optical axis, as illustrated in figure 3.16, is parabolic in shape. Hint: Since rays following different paths all move from the distant source to the focal point of the mirror, Fermat’s principle implies that all of these rays take the same time to do so (why is this?), and therefore all traverse the same distance.
Use Fermat’s principle to explain qualitatively why a ray of light follows the solid rather than the dashed line through the wedge of glass shown in figure 3.17.
Test your knowledge of Fermat’s principle by using equation (3.5.3) to derive Snell’s law.