4.5: Lorentz Contraction

Last updated
Save as PDF

Page ID: 32944

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

A similar argument can be made to show how the postulates of relativity result in the Lorentz contraction. Figure 4.8 compares the length X′ of a moving object measured in its own reference frame (left panel) with its length X as measured in a stationary reference frame (right panel). The length of a moving object is measured by simultaneously measuring the positions of the front and the rear of the object and subtracting these two numbers. Events A and C correspond to these position measurements for the stationary reference frame since they are respectively on the rear and front world lines of the object. Thus, the interval AC, which is equal to X, is the length of the object as measured in the stationary frame.

Figure 4.8: Definition sketch for understanding the Lorentz contraction. The parallel lines represent the world lines of the front and the rear of a moving object. The left panel shows a reference frame moving with the object, while the right panel shows a stationary reference frame.

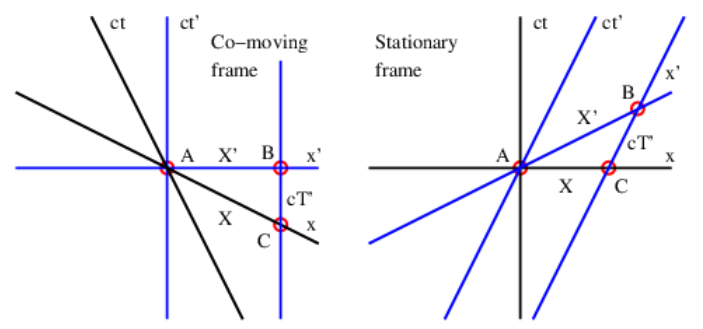
In the left panel, X is the hypotenuse of a right triangle. Therefore, by the Pythagorean theorem of spacetime, we have

\[X=I=\left(X^{\prime 2}-c^{2} T^{\prime 2}\right)^{1 / 2}\label{4.11}\]

Now, the line passing through A and C in the left panel is the line of simultaneity of the stationary reference frame. The slope of this line is -V∕c, where V is the speed of the object relative to the stationary reference frame. Geometrically in figure 4.8, the slope of this line is \(-\mathrm{cT}^{\prime} / \mathrm{X}^{\prime}\), so we find by equating these two expressions for the slope that

\[T^{\prime}=V X^{\prime} / c^{2}\label{4.12}\]

Finally, eliminating T′ between (\ref{4.11}) and (\ref{4.12}) results in

\[X=X^{\prime}\left(1-V^{2} / c^{2}\right)^{1 / 2}=X^{\prime} / \gamma\label{4.13}\]

This says that the length of a moving object as measured in a stationary reference frame (X) is less than the actual length of the object as measured in its own reference frame (X′). This reduction in length is called the Lorentz contraction.

Note that the Lorentz contraction only occurs in the direction of motion. The dimensions of a moving object perpendicular to the motion remain unchanged.