12.1: Energy Analysis

Last updated
Save as PDF

Page ID: 32998

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Figure 12.2: Potential, kinetic, and total energy of a harmonic oscillator plotted as a function of spring displacement x.

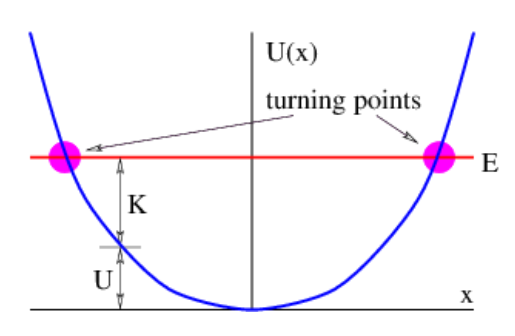
The potential energy of the mass-spring system is

\[U(x)=k x^{2} / 2\label{12.1}\]

which may be verified by noting that the Hooke’s law force is derived from this potential energy: \(F=-d\left(k x^{2} / 2\right) d x=-k x\). This is shown in figure 12.2. Since a potential energy exists, the total energy \(\mathrm{E}=\mathrm{K}+\mathrm{U}\) is conserved, i. e., is constant in time. If the total energy is known, this provides a useful tool for determining how the kinetic energy varies with the position x of the mass \(M: K(x)=E-U(x)\). Since the kinetic energy is expressed (non-relativistically) in terms of the velocity u as \(\mathrm{K}=\mathrm{Mu}^{2} / 2\), the velocity at any point on the graph in figure 12.2 is

\[u=\pm\left(\frac{2(E-U)}{M}\right)^{1 / 2}\label{12.2}\]

Given all this, it is fairly evident how the mass moves. From Hooke’s law, the mass is always accelerating toward the equilibrium position, x = 0. However, at any point the velocity can be either to the left or the right. At the points where \(U(x)=E\), the kinetic energy is zero. This occurs at the turning points

\[x_{T P}=\pm\left(\frac{2 E}{k}\right)^{1 / 2}\label{12.3}\]

If the mass is moving to the left, it slows down as it approaches the left turning point. It stops when it reaches this point and begins to move to the right. It accelerates until it passes the equilibrium position and then begins to decelerate, stopping at the right turning point, accelerating toward the left, etc. The mass thus oscillates between the left and right turning points. (Note that equations (\ref{12.2}) and (\ref{12.3}) are only true for the harmonic oscillator.)

How does the period of the oscillation depend on the total energy of the system? Notice that from equation (\ref{12.2}) the maximum speed of the mass (i. e., the speed at x = 0) is equal to \(\mathrm{u}_{\max }=(2 \mathrm{E} M)^{1 / 2}\). The average speed must be some fraction of this maximum value. Let us guess here that it is half the maximum speed:

\[u_{\text {average }} \approx \frac{u_{\max }}{2}=\left(\frac{E}{2 M}\right)^{1 / 2} \quad(\text { approximate }) .\label{12.4}\]

However, the distance d the mass has to travel for one full oscillation is twice the distance between turning points, or \(\mathrm{d}=4(2 \mathrm{E} / \mathrm{k})^{1 / 2}\). Therefore, the period of oscillation must be approximately

\[T=\frac{d}{u_{\text {average }}} \approx 4\left(\frac{2 E}{k}\right)^{1 / 2}\left(\frac{2 M}{E}\right)^{1 / 2}=8\left(\frac{M}{k}\right)^{1 / 2} \quad \text { (approximate) }\label{12.5}\]