12.3: Forced Oscillator

Last updated
Save as PDF

Page ID: 33000

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Figure 12.3: Illustration of a forced mass-spring oscillator. The left end of the spring is wiggled back and forth with an angular frequency \(\omega_{F}\) and a maximum amplitude \(\mathrm{d}_{0}\).

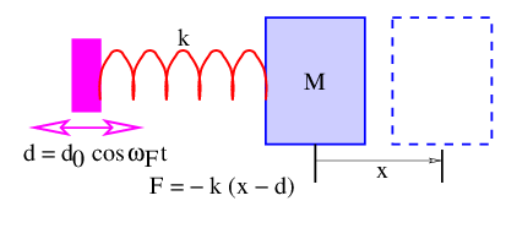
If we wiggle the left end of the spring by the amount \(\mathrm{d}=\mathrm{d}_{0} \cos \left(\omega_{\mathrm{F}} \mathrm{t}\right)\), as in figure 12.3, rather than rigidly fixing it as in figure 12.1, we have a forced harmonic oscillator. The constant \(\mathrm{d}_{0}\) is the amplitude of the imposed wiggling motion. The forcing frequency \(\omega_{F}\)is not necessarily equal to the natural or resonant frequency \(\omega=(\mathrm{k} / \mathrm{M})^{1 / 2}\) of the mass-spring system. Very different behavior occurs depending on whether \(\omega_{F}\)is less than, equal to, or greater than \(\omega\).

Given the above wiggling, the force of the spring on the mass becomes \(F=-k(x-d)=-k\left[x-d_{0} \cos \left(\omega_{F} t\right)\right]\) since the length of the spring is the difference between the positions of the left and right ends. Proceeding as for the unforced mass-spring system, we arrive at the differential equation

\[\frac{d^{2} x}{d t^{2}}+\frac{k x}{M}=\frac{k d_{0}}{M} \cos \left(\omega_{F} t\right)\label{12.10}\]

The solution to this equation turns out to be the sum of a forced part in which \(x\) is proportional to \(\cos \left(\omega_{F} t\right)\) and a free part which is the same as the solution to the unforced equation (12.2.4). We are primarily interested in the forced part of the solution, so let us set \(x=x_{0} \cos \left(\omega_{F} t\right)\) and substitute this into equation (\ref{12.10}):

\[-\omega_{F}^{2} x_{0} \cos \left(\omega_{F} t\right)+\frac{k x_{0}}{M} \cos \left(\omega_{F} t\right)=\frac{k d_{0}}{M} \cos \left(\omega_{F} t\right)\label{12.11}\]

Again the cosine factor cancels and we are left with an algebraic equation for x₀, the amplitude of the oscillatory motion of the mass.

Figure 12.4: Plot of the ratio of response to forcing vs. the ratio of forced to free oscillator frequency for the mass-spring system.

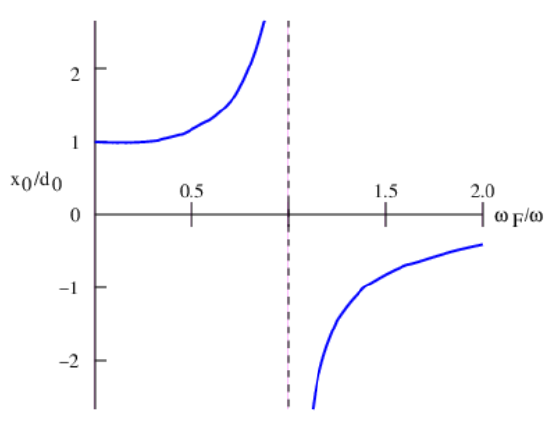
Solving for the ratio of the oscillation amplitude of the mass to the amplitude of the wiggling motion, \(\mathrm{x}_{0} / \mathrm{d}_{0}\), we find

\[\frac{x_{0}}{d_{0}}=\frac{1}{1-\omega_{F}^{2} / \omega^{2}}\label{12.12}\]

where we have recognized that \(k / M=\omega^{2}\), the square of the frequency of the free oscillation. This function is plotted in figure 12.4.

Notice that if \(\omega_{F}<\omega_{1}\), the motion of the mass is in phase with the wiggling motion and the amplitude of the mass oscillation is greater than the amplitude of the wiggling. As the forcing frequency approaches the natural frequency of the oscillator, the response of the mass grows in amplitude. When the forcing is at the resonant frequency, the response is technically infinite, though practical limits on the amplitude of the oscillation will intervene in this case — for instance, the spring cannot stretch or shrink an infinite amount. In many cases friction will act to limit the response of the mass to forcing near the resonant frequency. When the forcing frequency is greater than the natural frequency, the mass actually moves in the opposite direction of the wiggling motion — i. e., the response is out of phase with the forcing. The amplitude of the response decreases as the forcing frequency increases above the resonant frequency.

Forced and free harmonic oscillators form an important part of many physical systems. For instance, any elastic material body such as a bridge or an airplane wing has harmonic oscillatory modes. A common engineering problem is to ensure that such modes are damped by friction or some other physical mechanism when there is a possibility of exitation of these modes by naturally occurring processes. A number of disasters can be traced to a failure to properly account for oscillatory forcing in engineered structures.