12.6: Problems

Last updated
Save as PDF

Page ID: 33003

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

An oscillator (non-harmonic) has the potential energy function \(\mathrm{U}(\mathrm{x})=\mathrm{Cx}^{4}\), where C is a constant. How does the oscillation frequency depend on energy? Explain your reasoning.
Show that \(\mathrm{C} \cos (\omega \mathrm{t}-\phi)\) is an alternate way of writing \(A \sin (\omega t)+B \cos (\omega t)\) by finding the values of A and B in terms of the constants \(\mathrm{C} \text { and } \phi\). Hint: Expand \(\cos (\omega t-\phi)\) by using the trigonometric identity for the cosine of the sum of two angles.
If a mass-spring harmonic oscillator has displacement \(x=0\) and velocity \(\mathrm{dx} / \mathrm{dt}=\mathrm{V}\) at time \(\mathrm{t}=0\), determine the values of A and B as well as those of C and \(\phi\) in equation (12.2.4).
A mass M is suspended against gravity by a spring of spring constant k. The unstretched length of the spring is \(\mathrm{x}_{0}\) and under the influence of gravity the spring is stretched to a resting length \(x_{1}>x_{0}\).
1. Compute the length of the spring x₁ in the steady, resting case.
2. Set up the equation of motion for the mass moving under the influence of the two forces, gravity and spring. Solve the equation for the frequency of the oscillation and the position of the spring as a function of time x(t). Does the oscillation frequency change from the case without gravity?
Determine the two real solutions to the damped harmonic oscillator problem in the case in which \(\omega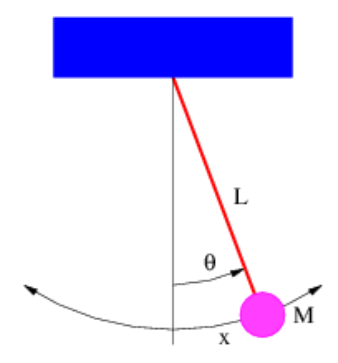_{0}^{2}<\beta^{2}\). Figure 12.5: The pendulum as a harmonic oscillator.
Consider the pendulum in figure 12.5. The mass M moves along an arc with x denoting the distance along the arc from the equilibrium point.
1. Find the component of the gravitational force tangent to the arc (and thus in the direction of motion of the mass) as a function of the angle \(theta\). Use the small angle approximation on \(\sin (\theta)\) to simplify this answer.
2. Get the force in terms of x rather than \(\theta\). (Recall that \(\theta=x / L\).)
3. Use Newton’s second law for motion in the x direction (i. e., along the arc followed by the mass) to get the equation of motion for the mass.
4. Solve the equation of motion using the solution to the mass-spring problem as a guide.
Forced damped oscillator:
1. Add a damping term to the forced harmonic oscillator equation (12.3.1) and solve for the forced part of the solution using complex exponential methods. Hint: Change the cosine on the right side of this equation to \(\exp \left(i \omega_{F} t\right)\) to convert the equation to complex form and then try the solution \(x=x_{0} \exp \left(i \omega_{F} t\right)\) where \(\mathrm{x}_{0}\) will depend of \(\omega_{F}\). Also, write the equation in terms of \(\beta=b /(2 M) \text { and } \omega^{2}=k / M\).
2. Find the physical part of this solution by taking the real part of x(t). Hint: While taking the real part of x, it may be helpful to recall that the inverse of any complex number can be written \(1 /(a+i b)=(a-i b) /\left(a^{2}+b^{2}\right)\).
3. Determine how \(\mathrm{x}_{0}\) differs from that in the undamped case when \(\omega_{F}\)is near the resonant frequency of the unforced oscillator. In particular, show how the phase and amplitude of the oscillation change as the forcing frequency changes from less than to greater than the resonant frequency.
A massless particle is confined to a box of length a. (Think of a photon between two mirrors.) Treating the particle classically, compute the period of one round trip from one end of the box to the other and back again. From this compute an angular frequency for the oscillation of this particle in the box. Does this frequency depend on the particle’s energy?
Compute the ground state energy \(\mathrm{E}_{\text {ground }}\) of a massless particle in a box of length a using quantum mechanics. Compare \(\mathrm{E}_{\text {ground }} / \hbar\) with the angular frequency computed in the previous problem.