11.10: Magnetic Forces and Fields (Exercise)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
11.3 Magnetic Fields and Lines
1. Discuss the similarities and differences between the electrical force on a charge and the magnetic force on a charge.
2. (a) Is it possible for the magnetic force on a charge moving in a magnetic field to be zero?
(b) Is it possible for the electric force on a charge moving in an electric field to be zero?
(c) Is it possible for the resultant of the electric and magnetic forces on a charge moving simultaneously through both fields to be zero?
11.4 Motion of a Charged Particle in a Magnetic Field
3. At a given instant, an electron and a proton are moving with the same velocity in a constant magnetic field. Compare the magnetic forces on these particles. Compare their accelerations.
4. Does increasing the magnitude of a uniform magnetic field through which a charge is traveling necessarily mean increasing the magnetic force on the charge? Does changing the direction of the field necessarily mean a change in the force on the charge?
5. An electron passes through a magnetic field without being deflected. What do you conclude about the magnetic field?
6. If a charged particle moves in a straight line, can you conclude that there is no magnetic field present?
7. How could you determine which pole of an electromagnet is north and which pole is south?
11.5 Magnetic Force on a Current-Carrying Conductor
8. Describe the error that results from accidently using your left rather than your right hand when determining the direction of a magnetic force.
9. Considering the magnetic force law, are the velocity and magnetic field always perpendicular? Are the force and velocity always perpendicular? What about the force and magnetic field?
10. Why can a nearby magnet distort a cathode ray tube television picture?
11. A magnetic field exerts a force on the moving electrons in a current carrying wire. What exerts the force on a wire?
12. There are regions where the magnetic field of earth is almost perpendicular to the surface of Earth. What difficulty does this cause in the use of a compass?
11.7 The Hall Effect
13. Hall potentials are much larger for poor conductors than for good conductors. Why?
11.8 Applications of Magnetic Forces and Fields
14. Describe the primary function of the electric field and the magnetic field in a cyclotron.
Problems
11.3 Magnetic Fields and Lines
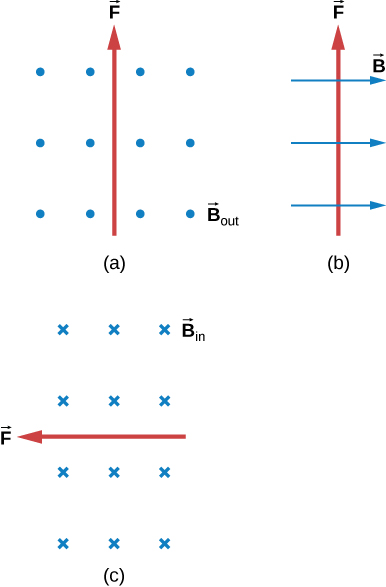
15. What is the direction of the magnetic force on a positive charge that moves as shown in each of the six cases?
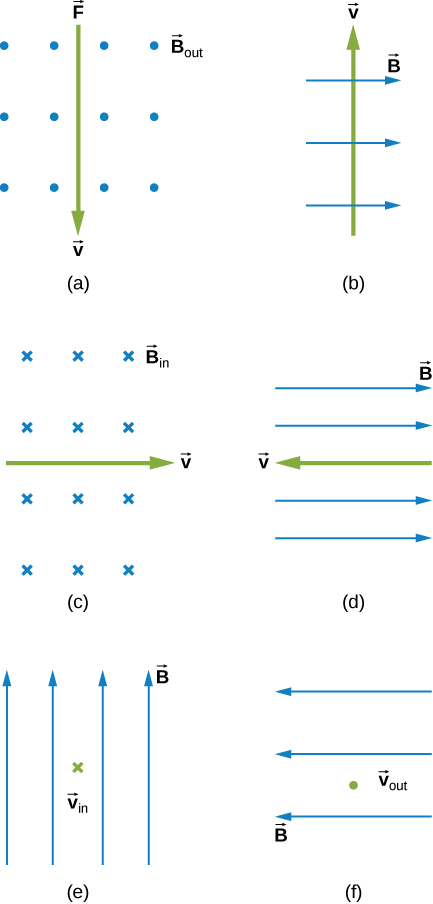
16. Repeat previous exercise for a negative charge.
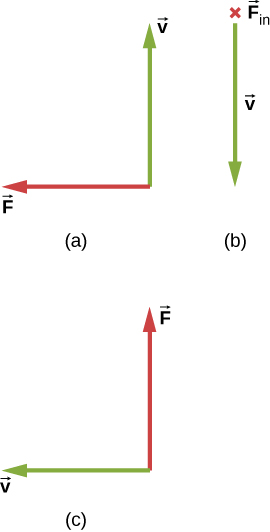
17. What is the direction of the velocity of a negative charge that experiences the magnetic force shown in each of the three cases, assuming it moves perpendicular to B?
18. Repeat previous exercise for a positive charge.
19. What is the direction of the magnetic field that produces the magnetic force on a positive charge as shown in each of the three cases, assuming B⃗ is perpendicular to v⃗ ?
20. Repeat previous exercise for a negative charge.
21. (a) Aircraft sometimes acquire small static charges. Suppose a supersonic jet has a 0.500-μC charge and flies due west at a speed of 660. m/s over Earth’s south magnetic pole, where the 8.00×10−5−T magnetic field points straight up. What are the direction and the magnitude of the magnetic force on the plane?
(b) Discuss whether the value obtained in part (a) implies this is a significant or negligible effect.
22. (a) A cosmic ray proton moving toward Earth at 5.00×107m/s experiences a magnetic force of 1.70×10−16N. What is the strength of the magnetic field if there is a 45º angle between it and the proton’s velocity?
(b) Is the value obtained in part a. consistent with the known strength of Earth’s magnetic field on its surface? Discuss.
23. An electron moving at 4.00×103m/s in a 1.25-T magnetic field experiences a magnetic force of 1.40×10−16N. What angle does the velocity of the electron make with the magnetic field? There are two answers.
24. (a) A physicist performing a sensitive measurement wants to limit the magnetic force on a moving charge in her equipment to less than 1.00×10−12N. What is the greatest the charge can be if it moves at a maximum speed of 30.0 m/s in Earth’s field?
(b) Discuss whether it would be difficult to limit the charge to less than the value found in (a) by comparing it with typical static electricity and noting that static is often absent.
11.4 Motion of a Charged Particle in a Magnetic Field
25. A cosmic-ray electron moves at 7.5×106m/s perpendicular to Earth’s magnetic field at an altitude where the field strength is 1.0×10−5T. What is the radius of the circular path the electron follows?
26. (a) Viewers of Star Trek have heard of an antimatter drive on the Starship Enterprise. One possibility for such a futuristic energy source is to store antimatter charged particles in a vacuum chamber, circulating in a magnetic field, and then extract them as needed. Antimatter annihilates normal matter, producing pure energy. What strength magnetic field is needed to hold antiprotons, moving at 5.0×107m/s in a circular path 2.00 m in radius? Antiprotons have the same mass as protons but the opposite (negative) charge.
(b) Is this field strength obtainable with today’s technology or is it a futuristic possibility?
27. (a) An oxygen-16 ion with a mass of 2.66×10−26kg travels at 5.0×106m/s perpendicular to a 1.20-T magnetic field, which makes it move in a circular arc with a 0.231-m radius. What positive charge is on the ion?
(b) What is the ratio of this charge to the charge of an electron? (c) Discuss why the ratio found in (b) should be an integer.
28. An electron in a TV CRT moves with a speed of 6.0×107m/s, in a direction perpendicular to Earth’s field, which has a strength of 5.0×10−5T. (a) What strength electric field must be applied perpendicular to the Earth’s field to make the electron moves in a straight line? (b) If this is done between plates separated by 1.00 cm, what is the voltage applied? (Note that TVs are usually surrounded by a ferromagnetic material to shield against external magnetic fields and avoid the need for such a correction.)
29. (a) At what speed will a proton move in a circular path of the same radius as the electron in the previous exercise?
(b) What would the radius of the path be if the proton had the same speed as the electron?
(c) What would the radius be if the proton had the same kinetic energy as the electron?
(d) The same momentum?
30. (a) What voltage will accelerate electrons to a speed of 6.00×10−7m/s? (b) Find the radius of curvature of the path of a proton accelerated through this potential in a 0.500-T field and compare this with the radius of curvature of an electron accelerated through the same potential.
31. An alpha-particle (m=6.64×10−27kg,q=3.2×10−19C) travels in a circular path of radius 25 cm in a uniform magnetic field of magnitude 1.5 T.
(a) What is the speed of the particle?
(b) What is the kinetic energy in electron-volts?
(c) Through what potential difference must the particle be accelerated in order to give it this kinetic energy?
32. A particle of charge q and mass m is accelerated from rest through a potential difference V, after which it encounters a uniform magnetic field B. If the particle moves in a plane perpendicular to B, what is the radius of its circular orbit?
11.5 Magnetic Force on a Current-Carrying Conductor
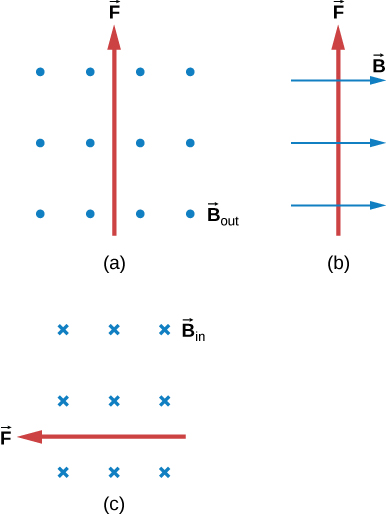
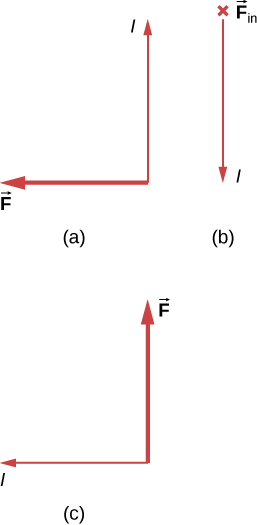
33. What is the direction of the magnetic force on the current in each of the six cases?
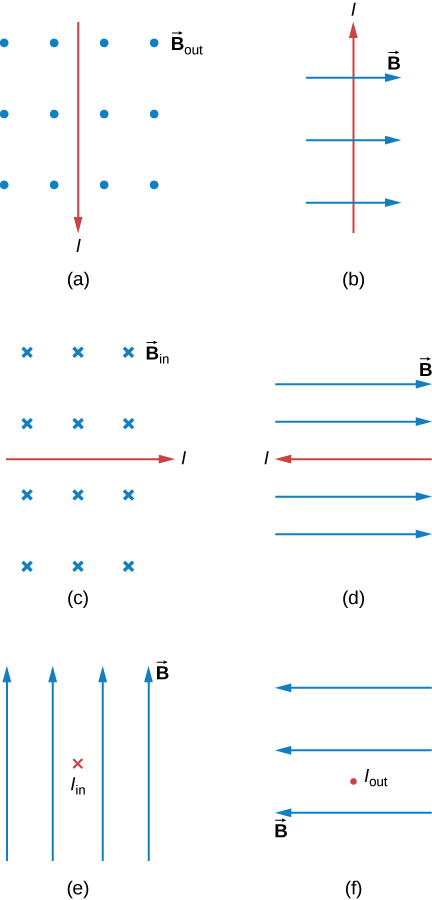
34. What is the direction of a current that experiences the magnetic force shown in each of the three cases, assuming the current runs perpendicular to B⃗ ?
35. What is the direction of the magnetic field that produces the magnetic force shown on the currents in each of the three cases, assuming B⃗ is perpendicular to I?
36. (a) What is the force per meter on a lightning bolt at the equator that carries 20,000 A perpendicular to Earth’s 3.0×10−5T field? (b) What is the direction of the force if the current is straight up and Earth’s field direction is due north, parallel to the ground?
37. (a) A dc power line for a light-rail system carries 1000 A at an angle of 30.0º to Earth’s 5.0×10−5T field. What is the force on a 100-m section of this line?
(b) Discuss practical concerns this presents, if any.
38. A wire carrying a 30.0-A current passes between the poles of a strong magnet that is perpendicular to its field and experiences a 2.16-N force on the 4.00 cm of wire in the field. What is the average field strength?
11.6 Force and Torque on a Current Loop
39. (a) By how many percent is the torque of a motor decreased if its permanent magnets lose 5.0% of their strength?
(b) How many percent would the current need to be increased to return the torque to original values?
40. (a) What is the maximum torque on a 150-turn square loop of wire 18.0 cm on a side that carries a 50.0-A current in a 1.60-T field?
(b) What is the torque when θ is 10.9º?
41. Find the current through a loop needed to create a maximum torque of 9.0N·m. The loop has 50 square turns that are 15.0 cm on a side and is in a uniform 0.800-T magnetic field.
42. Calculate the magnetic field strength needed on a 200-turn square loop 20.0 cm on a side to create a maximum torque of 300 N ⋅ m if the loop is carrying 25.0 A.
43. Since the equation for torque on a current-carrying loop is τ = NIAB sin θ, the units of N ⋅ m must equal units of A⋅m2T. Verify this.
44. (a) At what angle θ is the torque on a current loop 90.0% of maximum?
(b) 50.0% of maximum?
(c) 10.0% of maximum?
45. A proton has a magnetic field due to its spin. The field is similar to that created by a circular current loop 0.65×10−15m in radius with a current of 1.05×104A. Find the maximum torque on a proton in a 2.50-T field. (This is a significant torque on a small particle.)
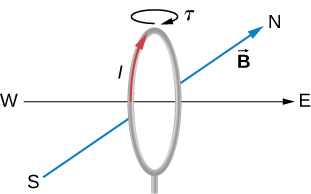
46. (a) A 200-turn circular loop of radius 50.0 cm is vertical, with its axis on an east-west line. A current of 100 A circulates clockwise in the loop when viewed from the east. Earth’s field here is due north, parallel to the ground, with a strength of 3.0×10−5T. What are the direction and magnitude of the torque on the loop?
(b) Does this device have any practical applications as a motor?
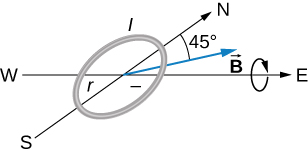
47. Repeat the previous problem, but with the loop lying flat on the ground with its current circulating counterclockwise (when viewed from above) in a location where Earth’s field is north, but at an angle 45.0° below the horizontal and with a strength of 6.0×10−5T.
11.7 The Hall Effect
48. A strip of copper is placed in a uniform magnetic field of magnitude 2.5 T. The Hall electric field is measured to be 1.5×10−3V/m.
(a) What is the drift speed of the conduction electrons?
(b) Assuming that n=8.0×1028electrons per cubic meter and that the cross-sectional area of the strip is 5.0×10−6m2, calculate the current in the strip.
(c) What is the Hall coefficient 1/nq?
49. The cross-sectional dimensions of the copper strip shown are 2.0 cm by 2.0 mm. The strip carries a current of 100 A, and it is placed in a magnetic field of magnitude B = 1.5 T. What are the value and polarity of the Hall potential in the copper strip?
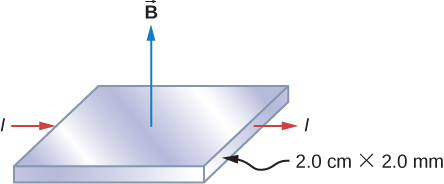
50. The magnitudes of the electric and magnetic fields in a velocity selector are 1.8×105V/m and 0.080 T, respectively.
(a) What speed must a proton have to pass through the selector?
(b) Also calculate the speeds required for an alpha-particle and a singly ionized sO16 atom to pass through the selector.
51. A charged particle moves through a velocity selector at constant velocity. In the selector, E=1.0×104N/C and B = 0.250 T. When the electric field is turned off, the charged particle travels in a circular path of radius 3.33 mm. Determine the charge-to-mass ratio of the particle.
52. A Hall probe gives a reading of 1.5μV for a current of 2 A when it is placed in a magnetic field of 1 T. What is the magnetic field in a region where the reading is 2μV for 1.7 A of current?
11.8 Applications of Magnetic Forces and Fields
53. A physicist is designing a cyclotron to accelerate protons to one-tenth the speed of light. The magnetic field will have a strength of 1.5 T. Determine
(a) the rotational period of the circulating protons and
(b) the maximum radius of the protons’ orbit.
54. The strengths of the fields in the velocity selector of a Bainbridge mass spectrometer are B = 0.500 T and E=1.2×105V/m, and the strength of the magnetic field that separates the ions is Bo=0.750T. A stream of singly charged Li ions is found to bend in a circular arc of radius 2.32 cm. What is the mass of the Li ions?
55. The magnetic field in a cyclotron is 1.25 T, and the maximum orbital radius of the circulating protons is 0.40 m.
(a) What is the kinetic energy of the protons when they are ejected from the cyclotron?
(b) What is this energy in MeV?
(c) Through what potential difference would a proton have to be accelerated to acquire this kinetic energy?
(d) What is the period of the voltage source used to accelerate the protons?
(e) Repeat the calculations for alpha-particles.
56. A mass spectrometer is being used to separate common oxygen-16 from the much rarer oxygen-18, taken from a sample of old glacial ice. (The relative abundance of these oxygen isotopes is related to climatic temperature at the time the ice was deposited.) The ratio of the masses of these two ions is 16 to 18, the mass of oxygen-16 is 2.66×10−26kg, and they are singly charged and travel at 5.00×106m/s in a 1.20-T magnetic field. What is the separation between their paths when they hit a target after traversing a semicircle?
57. (a) Triply charged uranium-235 and uranium-238 ions are being separated in a mass spectrometer. (The much rarer uranium-235 is used as reactor fuel.) The masses of the ions are 3.90×10−25kg and 3.95×10−25kg,respectively, and they travel at 3.0×105m/s in a 0.250-T field. What is the separation between their paths when they hit a target after traversing a semicircle? (b) Discuss whether this distance between their paths seems to be big enough to be practical in the separation of uranium-235 from uranium-238.
Additional Problems
58. Calculate the magnetic force on a hypothetical particle of charge 1.0×10−19C moving with a velocity of 6.0×104ˆim/s in a magnetic field of 1.2ˆkT.
59. Repeat the previous problem with a new magnetic field of (0.4ˆi+1.2ˆk)T.
60. An electron is projected into a uniform magnetic field (0.5ˆi+0.8ˆk)T with a velocity of (3.0ˆi+4.0ˆj)×106m/s. What is the magnetic force on the electron?
61. The mass and charge of a water droplet are 1.0×10−4g and 2.0×10−8C, respectively. If the droplet is given an initial horizontal velocity of 5.0×105ˆim/s, what magnetic field will keep it moving in this direction? Why must gravity be considered here?
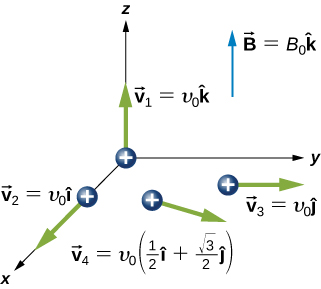
62. Four different proton velocities are given. For each case, determine the magnetic force on the proton in terms of e,v0, and B0.
63. An electron of kinetic energy 2000 eV passes between parallel plates that are 1.0 cm apart and kept at a potential difference of 300 V. What is the strength of the uniform magnetic field B that will allow the electron to travel undeflected through the plates? Assume E and B are perpendicular.
64. An alpha-particle (m=6.64×10−27kg,q=3.2×10−19C) moving with a velocity →v=(2.0ˆi−4.0ˆk)×106m/s enters a region where →E=(5.0ˆi−2.0ˆj)×104V/m and →B=(1.0ˆi+4.0ˆk)×10−2T. What is the initial force on it?
65. An electron moving with a velocity →v=(4.0ˆiˆ+3.0ˆjˆ+2.0ˆk)×106m/s enters a region where there is a uniform electric field and a uniform magnetic field. The magnetic field is given by →B=(1.0ˆi−2.0ˆj+4.0ˆk)×10−2T. If the electron travels through a region without being deflected, what is the electric field?
66. At a particular instant, an electron is traveling west to east with a kinetic energy of 10 keV. Earth’s magnetic field has a horizontal component of 1.8×10−5T north and a vertical component of 5.0×10−5T down. (a) What is the path of the electron? (b) What is the radius of curvature of the path?
67. What is the (a) path of a proton and (b) the magnetic force on the proton that is traveling west to east with a kinetic energy of 10 keV in Earth’s magnetic field that has a horizontal component of 1.8 x 10–5 T north and a vertical component of 5.0 x 10–5 T down?
68. What magnetic field is required in order to confine a proton moving with a speed of 4.0×106m/s to a circular orbit of radius 10 cm?
69. An electron and a proton move with the same speed in a plane perpendicular to a uniform magnetic field. Compare the radii and periods of their orbits.
70. A proton and an alpha-particle have the same kinetic energy and both move in a plane perpendicular to a uniform magnetic field. Compare the periods of their orbits.
71. A singly charged ion takes 2.0×10−3s to complete eight revolutions in a uniform magnetic field of magnitude 2.0×10−2T. What is the mass of the ion?
72. A particle moving downward at a speed of 6.0×106m/s enters a uniform magnetic field that is horizontal and directed from east to west.
(a) If the particle is deflected initially to the north in a circular arc, is its charge positive or negative?
(b) If B = 0.25 T and the charge-to-mass ratio (q/m) of the particle is 4.0×107C/kg, what is the radius of the path?
(c) What is the speed of the particle after it has moved in the field for 1.0×10−5s? for 2.0 s?
73. A proton, deuteron, and an alpha-particle are all accelerated through the same potential difference. They then enter the same magnetic field, moving perpendicular to it. Compute the ratios of the radii of their circular paths. Assume that md=2mp and mα=4mp.
74. A singly charged ion is moving in a uniform magnetic field of 7.5×10−2T completes 10 revolutions in 3.47×10−4s. Identify the ion.
75. Two particles have the same linear momentum, but particle A has four times the charge of particle B. If both particles move in a plane perpendicular to a uniform magnetic field, what is the ratio RA/RB of the radii of their circular orbits?
76. A uniform magnetic field of magnitude B is directed parallel to the z-axis. A proton enters the field with a velocity →v=(4ˆj+3ˆk)×106m/s and travels in a helical path with a radius of 5.0 cm.
(a) What is the value of B?
(b) What is the time required for one trip around the helix?
(c) Where is the proton 5.0×10−7s after entering the field?
77. An electron moving at 5.0×106m/s enters a magnetic field that makes a 75o angle with the x-axis of magnitude 0.20 T. Calculate the
(a) pitch and
(b) radius of the trajectory.
78. (a) A 0.750-m-long section of cable carrying current to a car starter motor makes an angle of 60º with Earth’s 5.5×10−5T field. What is the current when the wire experiences a force of 7.0×10−3N?
(b) If you run the wire between the poles of a strong horseshoe magnet, subjecting 5.00 cm of it to a 1.75-T field, what force is exerted on this segment of wire?
79. (a) What is the angle between a wire carrying an 8.00-A current and the 1.20-T field it is in if 50.0 cm of the wire experiences a magnetic force of 2.40 N?
(b) What is the force on the wire if it is rotated to make an angle of 90º with the field?
80. A 1.0-m-long segment of wire lies along the x-axis and carries a current of 2.0 A in the positive x-direction. Around the wire is the magnetic field of (3.0ˆi×4.0ˆk)×10−3T. Find the magnetic force on this segment.
81. A 5.0-m section of a long, straight wire carries a current of 10 A while in a uniform magnetic field of magnitude 8.0×10−3T. Calculate the magnitude of the force on the section if the angle between the field and the direction of the current is
(a) 45°;
(b) 90°;
(c) 0°; or
(d) 180°.
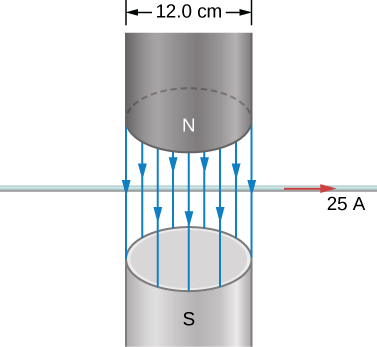
82. An electromagnet produces a magnetic field of magnitude 1.5 T throughout a cylindrical region of radius 6.0 cm. A straight wire carrying a current of 25 A passes through the field as shown in the accompanying figure. What is the magnetic force on the wire?
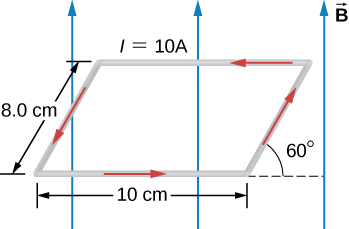
83. The current loop shown in the accompanying figure lies in the plane of the page, as does the magnetic field. Determine the net force and the net torque on the loop if I = 10 A and B = 1.5 T.
84. A circular coil of radius 5.0 cm is wound with five turns and carries a current of 5.0 A. If the coil is placed in a uniform magnetic field of strength 5.0 T, what is the maximum torque on it?
85. A circular coil of wire of radius 5.0 cm has 20 turns and carries a current of 2.0 A. The coil lies in a magnetic field of magnitude 0.50 T that is directed parallel to the plane of the coil.
(a) What is the magnetic dipole moment of the coil?
(b) What is the torque on the coil?
86. A current-carrying coil in a magnetic field experiences a torque that is 75% of the maximum possible torque. What is the angle between the magnetic field and the normal to the plane of the coil?
87. A 4.0-cm by 6.0-cm rectangular current loop carries a current of 10 A. What is the magnetic dipole moment of the loop?
88. A circular coil with 200 turns has a radius of 2.0 cm.
(a) What current through the coil results in a magnetic dipole moment of 3.0 Am2?
(b) What is the maximum torque that the coil will experience in a uniform field of strength 5.0×10−2T?
(c) If the angle between μ and B is 45°, what is the magnitude of the torque on the coil?
(d) What is the magnetic potential energy of coil for this orientation?
89. The current through a circular wire loop of radius 10 cm is 5.0 A.
(a) Calculate the magnetic dipole moment of the loop.
(b) What is the torque on the loop if it is in a uniform 0.20-T magnetic field such that μ and B are directed at 30° to each other?
(c) For this position, what is the potential energy of the dipole?
90. A wire of length 1.0 m is wound into a single-turn planar loop. The loop carries a current of 5.0 A, and it is placed in a uniform magnetic field of strength 0.25 T.
(a) What is the maximum torque that the loop will experience if it is square?
(b) If it is circular?
(c) At what angle relative to B would the normal to the circular coil have to be oriented so that the torque on it would be the same as the maximum torque on the square coil?
91. Consider an electron rotating in a circular orbit of radius r. Show that the magnitudes of the magnetic dipole moment μ and the angular momentum L of the electron are related by:
μL=e2m.
92. The Hall effect is to be used to find the sign of charge carriers in a semiconductor sample. The probe is placed between the poles of a magnet so that magnetic field is pointed up. A current is passed through a rectangular sample placed horizontally. As current is passed through the sample in the east direction, the north side of the sample is found to be at a higher potential than the south side. Decide if the number density of charge carriers is positively or negatively charged.
93. The density of charge carriers for copper is 8.47×1028 electrons per cubic meter. What will be the Hall voltage reading from a probe made up of 3cm×2 cm×1 cm(L×W×T) copper plate when a current of 1.5 A is passed through it in a magnetic field of 2.5 T perpendicular to the 3cm×2 cm.
94. The Hall effect is to be used to find the density of charge carriers in an unknown material. A Hall voltage 40 μV for 3-A current is observed in a 3-T magnetic field for a rectangular sample with length 2 cm, width 1.5 cm, and height 0.4 cm. Determine the density of the charge carriers.
95. Show that the Hall voltage across wires made of the same material, carrying identical currents, and subjected to the same magnetic field is inversely proportional to their diameters. (Hint: Consider how drift velocity depends on wire diameter.)
96. A velocity selector in a mass spectrometer uses a 0.100-T magnetic field.
(a) What electric field strength is needed to select a speed of 4.0×106m/s?
(b) What is the voltage between the plates if they are separated by 1.00 cm?
97. Find the radius of curvature of the path of a 25.0-MeV proton moving perpendicularly to the 1.20-T field of a cyclotron.
98. Unreasonable results To construct a non-mechanical water meter, a 0.500-T magnetic field is placed across the supply water pipe to a home and the Hall voltage is recorded.
(a) Find the flow rate through a 3.00-cm-diameter pipe if the Hall voltage is 60.0 mV.
(b) What would the Hall voltage be for the same flow rate through a 10.0-cm-diameter pipe with the same field applied?
99. Unreasonable results A charged particle having mass 6.64×10−27kg (that of a helium atom) moving at 8.70×105m/s perpendicular to a 1.50-T magnetic field travels in a circular path of radius 16.0 mm.
(a) What is the charge of the particle?
(b) What is unreasonable about this result?
(c) Which assumptions are responsible?
100. Unreasonable results An inventor wants to generate 120-V power by moving a 1.00-m-long wire perpendicular to Earth’s 5.00×10−5T field.
(a) Find the speed with which the wire must move.
(b) What is unreasonable about this result? (c) Which assumption is responsible?
101. Unreasonable results Frustrated by the small Hall voltage obtained in blood flow measurements, a medical physicist decides to increase the applied magnetic field strength to get a 0.500-V output for blood moving at 30.0 cm/s in a 1.50-cm-diameter vessel.
(a) What magnetic field strength is needed?
(b) What is unreasonable about this result?
(c) Which premise is responsible?
Challenge Problems
102. A particle of charge +q and mass m moves with velocity ^v0 pointed in the +y-direction as it crosses the x-axis at x = R at a particular time. There is a negative charge –Q fixed at the origin, and there exists a uniform magnetic field ^B0 pointed in the +z-direction. It is found that the particle describes a circle of radius R about –Q. Find ^B0 in terms of the given quantities.
103. A proton of speed v=6×105m/s enters a region of uniform magnetic field of B = 0.5 T at an angle of \displaystyle q=30° to the magnetic field. In the region of magnetic field proton describes a helical path with radius R and pitch p (distance between loops). Find R and p.
104. A particle’s path is bent when it passes through a region of non-zero magnetic field although its speed remains unchanged. This is very useful for “beam steering” in particle accelerators. Consider a proton of speed \displaystyle 4×10^6m/s entering a region of uniform magnetic field 0.2 T over a 5-cm-wide region. Magnetic field is perpendicular to the velocity of the particle. By how much angle will the path of the proton be bent? (Hint: The particle comes out tangent to a circle.)
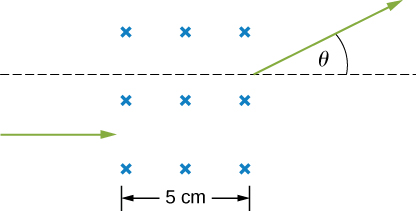
105. In a region a non-uniform magnetic field exists such that \displaystyle B_x=0,B_y=0, and \displaystyle B_z=ax, where a is a constant. At some time t, a wire of length L is carrying a current I is located along the x-axis from origin to x = L. Find the magnetic force on the wire at this instant in time.
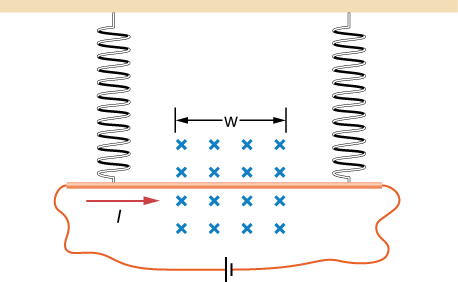
106. A copper rod of mass m and length L is hung from the ceiling using two springs of spring constant k. A uniform magnetic field of magnitude \displaystyle B_0 pointing perpendicular to the rod and spring (coming out of the page in the figure) exists in a region of space covering a length w of the copper rod. The ends of the rod are then connected by flexible copper wire across the terminals of a battery of voltage V. Determine the change in the length of the springs when a current I runs through the copper rod in the direction shown in figure. (Ignore any force by the flexible wire.)
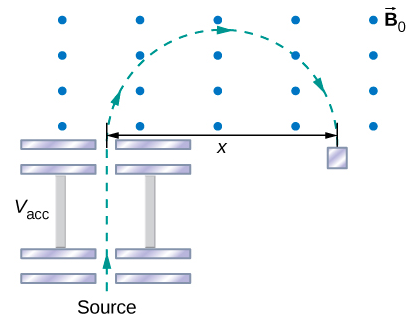
107. The accompanied figure shows an arrangement for measuring mass of ions by an instrument called the mass spectrometer. An ion of mass m and charge +q is produced essentially at rest in source S, a chamber in which a gas discharge is taking place. The ion is accelerated by a potential difference \displaystyle V_{acc} and allowed to enter a region of constant magnetic field \displaystyle \vec{B_0}. In the uniform magnetic field region, the ion moves in a semicircular path striking a photographic plate at a distance x from the entry point. Derive a formula for mass m in terms of \displaystyle B_0, q, V_{acc}, and \displaystyle x.
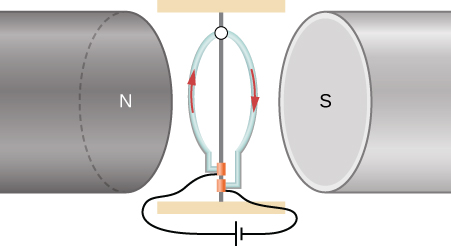
108. A wire is made into a circular shape of radius R and pivoted along a central support. The two ends of the wire are touching a brush that is connected to a dc power source. The structure is between the poles of a magnet such that we can assume there is a uniform magnetic field on the wire. In terms of a coordinate system with origin at the center of the ring, magnetic field is \displaystyle B_x=B_0,B_y=B_z=0, and the ring rotates about the z-axis. Find the torque on the ring when it is not in the xz-plane.
109. A long-rigid wire lies along the x-axis and carries a current of 2.5 A in the positive x-direction. Around the wire is the magnetic field \displaystyle \vec{B} =2.0\hat{i}+5.0x^2\hat{j}, with x in meters and B in millitesla. Calculate the magnetic force on the segment of wire between x = 2.0 m and x = 4.0 m.
110. A circular loop of wire of area 10 \displaystyle cm^2 carries a current of 25 A. At a particular instant, the loop lies in the xy-plane and is subjected to a magnetic field \displaystyle \vec{B} =(2.0\hat{i}+6.0\hat{j}+8.0\hat{k})×10^{−3}T. As viewed from above the xy-plane, the current is circulating clockwise.
(a) What is the magnetic dipole moment of the current loop?
(b) At this instant, what is the magnetic torque on the loop?


