5.4: Coulomb's Law
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Describe the electric force, both qualitatively and quantitatively
- Calculate the force that charges exert on each other
- Determine the direction of the electric force for different source charges
- Correctly describe and apply the superposition principle for multiple source charges
Experiments with electric charges have shown that if two objects each have electric charge, then they exert an electric force on each other. The magnitude of the force is linearly proportional to the net charge on each object and inversely proportional to the square of the distance between them. (Interestingly, the force does not depend on the mass of the objects.) The direction of the force vector is along the imaginary line joining the two objects and is dictated by the signs of the charges involved.
Let
- q1,q2= the net electric charge of the two objects;
- →r12= the vector displacement from q1 to q2.
The electric force →F on one of the charges is proportional to the magnitude of its own charge and the magnitude of the other charge, and is inversely proportional to the square of the distance between them:
F∝q1q2r212.
This proportionality becomes an equality with the introduction of a proportionality constant. For reasons that will become clear in a later chapter, the proportionality constant that we use is actually a collection of constants. (We discuss this constant shortly.)
The magnitude of the electric force (or Coulomb force) between two electrically charged particles is equal to
|F12|=14πε0|q1q2|r212
The unit vector r has a magnitude of 1 and points along the axis as the charges. If the charges have the same sign, the force is in the same direction as r showing a repelling force. If the charges have different signs, the force is in the opposite direction of r showing an attracting force. (Figure 5.4.1).
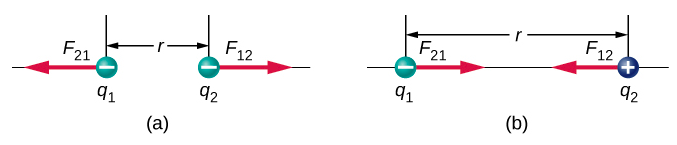
It is important to note that the electric force is not constant; it is a function of the separation distance between the two charges. If either the test charge or the source charge (or both) move, then →r changes, and therefore so does the force. An immediate consequence of this is that direct application of Newton’s laws with this force can be mathematically difficult, depending on the specific problem at hand. It can (usually) be done, but we almost always look for easier methods of calculating whatever physical quantity we are interested in. (Conservation of energy is the most common choice.)
Finally, the new constant ϵ0 in Coulomb’s law is called the permittivity of free space, or (better) the permittivity of vacuum. It has a very important physical meaning that we will discuss in a later chapter; for now, it is simply an empirical proportionality constant. Its numerical value (to three significant figures) turns out to be
ϵ0=8.85×10−12C2N⋅m2.
These units are required to give the force in Coulomb’s law the correct units of newtons. Note that in Coulomb’s law, the permittivity of vacuum is only part of the proportionality constant. For convenience, we often define a Coulomb’s constant:
ke=14πϵ0=8.99×109N⋅m2C2.
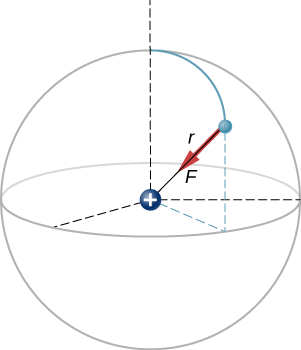
A hydrogen atom consists of a single proton and a single electron. The proton has a charge of +e and the electron has −e. In the “ground state” of the atom, the electron orbits the proton at most probable distance of 5.29×10−11m (Figure 5.4.2). Calculate the electric force on the electron due to the proton.
Strategy
For the purposes of this example, we are treating the electron and proton as two point particles, each with an electric charge, and we are told the distance between them; we are asked to calculate the force on the electron. We thus use Coulomb’s law (Equation ???).
Solution
Our two charges are,
q1=+e=+1.602×10−19Cq2=−e=−1.602×10−19C
and the distance between them
r=5.29×10−11m.
The magnitude of the force on the electron (Equation ???) is
F=14πϵ0|q1q2|r212=14π(8.85×10−12C2N⋅m2)(1.602×10−19C)2(5.29×10−11m)2=8.25×10−8N.
As for the direction, since the charges on the two particles are opposite, the force is attractive; the force on the electron points radially directly toward the proton, everywhere in the electron’s orbit. The force is thus expressed as
→F=(8.25×10−8N)ˆr.
Significance
This is a three-dimensional system, so the electron (and therefore the force on it) can be anywhere in an imaginary spherical shell around the proton. In this “classical” model of the hydrogen atom, the electrostatic force on the electron points in the inward centripetal direction, thus maintaining the electron’s orbit. But note that the quantum mechanical model of hydrogen (discussed in Quantum Mechanics) is utterly different.
What would be different if the electron also had a positive charge?
- Answer
-
The force would point outward.
Multiple Source Charges
The analysis that we have done for two particles can be extended to an arbitrary number of particles; we simply repeat the analysis, two charges at a time. Specifically, we ask the question: Given N charges (which we refer to as source charge), what is the net electric force that they exert on some other point charge (which we call the test charge)? Note that we use these terms because we can think of the test charge being used to test the strength of the force provided by the source charges.
Like all forces that we have seen up to now, the net electric force on our test charge is simply the vector sum of each individual electric force exerted on it by each of the individual test charges. Thus, we can calculate the net force on the test charge Q by calculating the force on it from each source charge, taken one at a time, and then adding all those forces together (as vectors). This ability to simply add up individual forces in this way is referred to as the principle of superposition, and is one of the more important features of the electric force. In mathematical form, this becomes
→F(r)=14πϵ0QN∑i=1qir2iˆr2i.
In this expression, Q represents the charge of the particle that is experiencing the electric force →F, and is located at →r from the origin; the qi's are the N source charges, and the vectors →ri=riˆri are the displacements from the position of the ith charge to the position of Q. Each of the N unit vectors points directly from its associated source charge toward the test charge. All of this is depicted in Figure 5.4.3. Please note that there is no physical difference between Q and qi; the difference in labels is merely to allow clear discussion, with Q being the charge we are determining the force on.
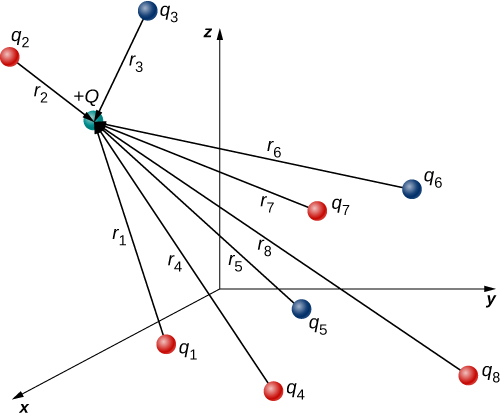
(Note that the force vector →Fi does not necessarily point in the same direction as the unit vector ˆri; it may point in the opposite direction, −ˆri. The signs of the source charge and test charge determine the direction of the force on the test charge.)
There is a complication, however. Just as the source charges each exert a force on the test charge, so too (by Newton’s third law) does the test charge exert an equal and opposite force on each of the source charges. As a consequence, each source charge would change position. However, by Equation ???, the force on the test charge is a function of position; thus, as the positions of the source charges change, the net force on the test charge necessarily changes, which changes the force, which again changes the positions. Thus, the entire mathematical analysis quickly becomes intractable. Later, we will learn techniques for handling this situation, but for now, we make the simplifying assumption that the source charges are fixed in place somehow, so that their positions are constant in time. (The test charge is allowed to move.) With this restriction in place, the analysis of charges is known as electrostatics, where “statics” refers to the constant (that is, static) positions of the source charges and the force is referred to as an electrostatic force.
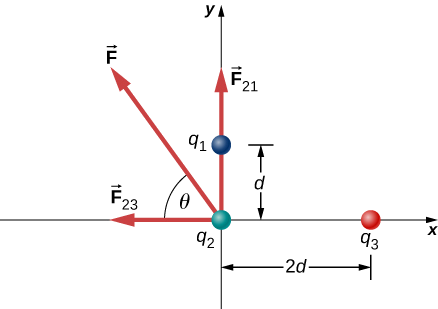
Three different, small charged objects are placed as shown in Figure 5.4.4. The charges q1 and q3 are fixed in place; q2 is free to move. Given q1=2e,q2=−3e, and q3=−5e, and that d=2.0×10−7m, what is the net force on the middle charge q2?
Strategy
We use Coulomb’s law again. The way the question is phrased indicates that q2 is our test charge, so that q1 and q3 are source charges. The principle of superposition says that the force on q2 from each of the other charges is unaffected by the presence of the other charge. Therefore, we write down the force on q2 from each and add them together as vectors.
Solution
We have two source charges q1 and q3 a test charge q2, distances r21 and r23 and we are asked to find a force. This calls for Coulomb’s law and superposition of forces. There are two forces:
→F=→F21+→F23=14πϵ0[q2q1r221ˆj+(−q2q3r223ˆi)].
We cannot add these forces directly because they don’t point in the same direction: →F12 points only in the −x-direction, while →F13 points only in the +y-direction. The net force is obtained from applying the Pythagorean theorem to its x- and y-components:
F=√F2x+F2y
and
Fx=−F23=−14πϵ0q2q3r223=−(8.99×109N⋅m2C2)(4.806×10−19C)(8.01×10−19C)(4.00×10−7m)2=−2.16×10−14N
and
Fy=F21=14πϵ0q2q1r21=(9.99×109N⋅m2C2)(4.806×10−19C)(3.204×10−19C)(2.00×10−7m)2=3.46×10−14N.
We find that
F=√F2x+F2y=4.08×10−14N
at an angle of
ϕ=tan−1(FyFx)=tan−1(3.46×10−14N−2.16×10−14N)=−58∘,
that is, 58∘ above the −x-axis, as shown in the diagram.
Significance
Notice that when we substituted the numerical values of the charges, we did not include the negative sign of either q1 or q3. Recall that negative signs on vector quantities indicate a reversal of direction of the vector in question. But for electric forces, the direction of the force is determined by the types (signs) of both interacting charges; we determine the force directions by considering whether the signs of the two charges are the same or are opposite. If you also include negative signs from negative charges when you substitute numbers, you run the risk of mathematically reversing the direction of the force you are calculating. Thus, the safest thing to do is to calculate just the magnitude of the force, using the absolute values of the charges, and determine the directions physically.
It’s also worth noting that the only new concept in this example is how to calculate the electric forces; everything else (getting the net force from its components, breaking the forces into their components, finding the direction of the net force) is the same as force problems you have done earlier.
What would be different in Example 5.4.2 if q1 were negative rather than positive?
- Answer
-
The net force would point 58∘ below the −x-axis.


