8.4: Energy Stored in a Capacitor
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Explain how energy is stored in a capacitor
- Use energy relations to determine the energy stored in a capacitor network
Most of us have seen dramatizations of medical personnel using a defibrillator to pass an electrical current through a patient’s heart to get it to beat normally. Often realistic in detail, the person applying the shock directs another person to “make it 400 joules this time.” The energy delivered by the defibrillator is stored in a capacitor and can be adjusted to fit the situation. SI units of joules are often employed. Less dramatic is the use of capacitors in microelectronics to supply energy when batteries are charged (Figure 8.4.1). Capacitors are also used to supply energy for flash lamps on cameras.

The energy UC stored in a capacitor is electrostatic potential energy and is thus related to the charge Q and voltage V between the capacitor plates. A charged capacitor stores energy in the electrical field between its plates. As the capacitor is being charged, the electrical field builds up. When a charged capacitor is disconnected from a battery, its energy remains in the field in the space between its plates.
To gain insight into how this energy may be expressed (in terms of Q and V), consider a charged, empty, parallel-plate capacitor; that is, a capacitor without a dielectric but with a vacuum between its plates. The space between its plates has a volume Ad, and it is filled with a uniform electrostatic field E. The total energy UC of the capacitor is contained within this space. The energy density uE in this space is simply UC divided by the volume Ad. If we know the energy density, the energy can be found as UC=uE(Ad). We will learn in Electromagnetic Waves (after completing the study of Maxwell’s equations) that the energy density uE in a region of free space occupied by an electrical field E depends only on the magnitude of the field and is
uE=12ϵ0E2.
If we multiply the energy density by the volume between the plates, we obtain the amount of energy stored between the plates of a parallel-plate capacitor UC=uE(Ad)=12ϵ0E2Ad=12ϵ0V2d2Ad=12V2ϵ0Ad=12V2C.
In this derivation, we used the fact that the electrical field between the plates is uniform so that E=V/d and C=ϵ0A/d. Because C=Q/V, we can express this result in other equivalent forms:
UC=12V2C=12Q2C=12QV.
The expression in Equation ??? for the energy stored in a parallel-plate capacitor is generally valid for all types of capacitors. To see this, consider any uncharged capacitor (not necessarily a parallel-plate type). At some instant, we connect it across a battery, giving it a potential difference V=q/C between its plates. Initially, the charge on the plates is Q=0. As the capacitor is being charged, the charge gradually builds up on its plates, and after some time, it reaches the value Q. To move an infinitesimal charge dq from the negative plate to the positive plate (from a lower to a higher potential), the amount of work dW that must be done on dq is dW=Wdq=qCdq.
This work becomes the energy stored in the electrical field of the capacitor. In order to charge the capacitor to a charge Q, the total work required is
W=∫W(Q)0dW=∫Q0qCdq=12Q2C.
Since the geometry of the capacitor has not been specified, this equation holds for any type of capacitor. The total work W needed to charge a capacitor is the electrical potential energy UC stored in it, or UC=W. When the charge is expressed in coulombs, potential is expressed in volts, and the capacitance is expressed in farads, this relation gives the energy in joules.
Knowing that the energy stored in a capacitor is UC=Q2/(2C), we can now find the energy density uE stored in a vacuum between the plates of a charged parallel-plate capacitor. We just have to divide UC by the volume Ad of space between its plates and take into account that for a parallel-plate capacitor, we have E=σ/ϵ0 and C=ϵ0A/d. Therefore, we obtain
uE=UCAd=12Q2C1Ad=12Q2ϵ0A/d1Ad=121ϵ0(QA)2=σ22ϵ0=(Eϵ0)22ϵ0=ϵ02E2
We see that this expression for the density of energy stored in a parallel-plate capacitor is in accordance with the general relation expressed in Equation ???. We could repeat this calculation for either a spherical capacitor or a cylindrical capacitor—or other capacitors—and in all cases, we would end up with the general relation given by Equation ???.
Calculate the energy stored in the capacitor network in Figure 8.3.4a when the capacitors are fully charged and when the capacitances are C1=12.0μF,C2=2.0μF, and C3=4.0μF, respectively.
Strategy
We use Equation ??? to find the energy U1,U2, and U3 stored in capacitors 1, 2, and 3, respectively. The total energy is the sum of all these energies.
Solution We identify C1=12.0μF and V1=4.0V,C2=2.0μF and V2=8.0V,C3=4.0μF and V3=8.0V. The energies stored in these capacitors are
U1=12C1V21=12(12.0μF)(4.0V)2=96μJ,
U2=12C2V22=12(2.0μF)(8.0V)2=64μJ,
U3=12C3V23=12(4.0μF)(8.0V)2=130μJ,
The total energy stored in this network is
UC=U1+U2+U3=96μJ+64μJ+130μJ=0.29mJ.
Significance
We can verify this result by calculating the energy stored in the single 4.0−μF capacitor, which is found to be equivalent to the entire network. The voltage across the network is 12.0 V. The total energy obtained in this way agrees with our previously obtained result, UC=12CV2=12(4.0μF)(12.0V)2=0.29mJ
The potential difference across a 5.0-pF capacitor is 0.40 V. (a) What is the energy stored in this capacitor? (b) The potential difference is now increased to 1.20 V. By what factor is the stored energy increased?
- Answer
-
a. 4.0×10−13J; b. 9 times
In a cardiac emergency, a portable electronic device known as an automated external defibrillator (AED) can be a lifesaver. A defibrillator (Figure 8.4.2) delivers a large charge in a short burst, or a shock, to a person’s heart to correct abnormal heart rhythm (an arrhythmia). A heart attack can arise from the onset of fast, irregular beating of the heart—called cardiac or ventricular fibrillation. Applying a large shock of electrical energy can terminate the arrhythmia and allow the body’s natural pacemaker to resume its normal rhythm. Today, it is common for ambulances to carry AEDs. AEDs are also found in many public places. These are designed to be used by lay persons. The device automatically diagnoses the patient’s heart rhythm and then applies the shock with appropriate energy and waveform. CPR (cardiopulmonary resuscitation) is recommended in many cases before using a defibrillator.
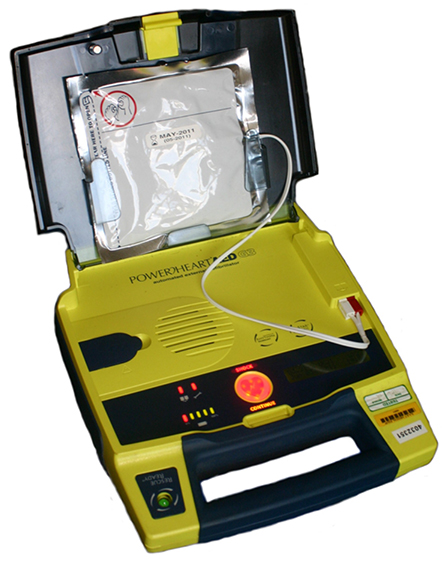
A heart defibrillator delivers 4.00×102J of energy by discharging a capacitor initially at 1.00×104V. What is its capacitance?
Strategy
We are given UC and V, and we are asked to find the capacitance C. We solve Equation ??? for C and substitute.
Solution
Solving this expression for C and entering the given values yields C=2UCV2=24.00×102J(1.00×104V)2=8.00μF.


