2.4: An Example
( \newcommand{\kernel}{\mathrm{null}\,}\)
Feeling It In Your Bones
 2-1
2-1
We will discuss the physics of forced oscillations further in the context of the simple system shown in Figure 2.9. The block has mass m. The block moves in a viscous fluid that provides a frictional force. We will imagine that the fluid is something like a thick silicone oil, so that the steady state solution is reached very quickly. The block is attached to a cord that runs over a pulley and is attached to a spring, as shown. The spring has spring constant K. You hold on to the other end of the spring and move it back and forth with displacement d0cosωdt.
d0 cos ωdt . (2.35) In this arrangement, you don’t have to be in the viscous fluid with the block — this makes it a lot easier to breathe.
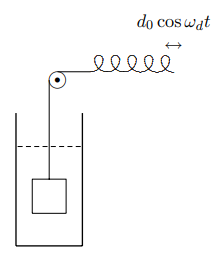
Figure 2.9: An oscillator that is damped by moving in a viscous fluid.
The question is, how does the block move? This system actually has exactly the equation of motion of the forced, damped oscillator. To see this, note that the change in the length of the spring from its equilibrium length is the difference, x(t)−d0cosωdt.
Thus the equation motion looks like this: md2dt2x(t)+mΓddtx(t)=−K[x(t)−d0cosωdt].
Dividing by m and rearranging terms, you can see that this is identical to (2.14) with F0/m=Kd0/m=ω20d0.
Moving the other end of the spring sinusoidally effectively produces a sinusoidally varying force on the mass.
Now we will go over the solution again, stressing the physics of this system as we go. Try to imagine yourself actually doing the experiment! It will help to try to feel the forces involved in your bones. It may help to check out program 2-1 on the supplementary programs disk. This allows you to see the effect, but you should really try to feel it!
The first step is to go over to the complex force, as in (2.16). The result looks like
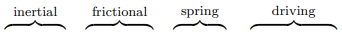
d2dt2z(t)+Γddtz(t)+ω20z(t)=ω20d0e−iωdt
We have labeled the terms in (2.39) to remind you of their different physical origins.
The next step is to look for irreducible steady state solutions of the form of (2.19): z(t)=Ae−iωdt.
Inserting (2.40) into (2.39), we get [−ω2d−iΓωd+ω20]Ae−iωdt=ω20d0e−iωdt.
What we will discuss in detail is the phase of the quantity in square brackets on the left-hand side of (2.41). Each of the three terms, inertial, frictional and spring, has a different phase. Each term also depends on the angular frequency, ωd in a different way. The phase of A depends on which term dominates.
For very small ωd, in particular for ωd≪ω0,Γ,
the spring term dominates the sum. Then A is in phase with the driving force. This has a simple physical interpretation. If you move the end of the spring slowly enough, both friction and inertia are irrelevant. When the block is moving very slowly, a vanishingly small force is required. The block just follows along with the displacement of the end of the spring, A≈d0. You should be able to feel this dependence in your bones. If you move your hand very slowly, the mass has no trouble keeping up with you.
For very large ωd, that is for ωd≫ω0,Γ,
the inertial term dominates the sum. The displacement is then 180∘ out of phase with the driving force. It also gets smaller and smaller as ωd increases, going like A≈−ω20ω2dd0.
Again, this makes sense physically. When the angular frequency of the driving force gets very large, the mass just doesn’t have time to move.
In between, at least two of the three terms on the left-hand side of (2.41) contribute significantly to the sum. At resonance, the inertial term exactly cancels the spring term, leaving only the frictional term, so that the displacement is 90∘ out of phase with the driving force. The size of the damping force determines how sharp the resonance is. If ¡ is much smaller than ω0, then the cancellation between the inertial and spring terms in (2.39) must be very precise in order for the frictional term to dominate. In this case, the resonance is very sharp. On the other hand, if Γ≫ω0, the resonance is very broad, and the enhancement at resonance is not very large, because the frictional term dominates for a large range of ωd around the point of resonance, ωd=ω0.
Try it! There is no substitute for actually doing this experiment. It will really give you a feel for what resonance is all about. Start by moving your hand at a very low frequency, so that the block stays in phase with the motion of your hand. Then very gradually increase the frequency. If you change the frequency slowly enough, the contributions from the transient free oscillation will be small, and you will stay near the steady state solution. As the frequency increases, you will first see that because of friction, the block starts to lag behind your hand. As you go through resonance, this lag will increase and go through 90∘. Finally at very high frequency, the block will be 180∘ out of phase with your hand and its displacement (the amplitude of its motion) will be very small.


