9.1: Reflection and Transmission

Forced Oscillation

Consider the forced oscillation problem in a semiinfinite stretched string that runs from \(x = 0\) to \(x = \infty\). Suppose that \[\psi(0, t)=A \cos \omega t\]

Then what is \(\psi(x,t)\)? This is not a well-posed problem, because we only have a boundary condition on one side. Furthermore, \(\psi(\infty, t)\) does not have a definite value. We can only talk about the value of a function at infinity if the function goes to a constant value. Here, we expect \(\psi(x,t)\) to continue to oscillate as \(x \rightarrow \infty\), so we cannot specify it. Instead, we can specify either the incoming (traveling toward the boundary at \(x = 0\) in the \(- x\) direction) or the outgoing (traveling away from \(x = 0\) in the \(+ x\) direction) traveling waves in the system. This is called a “boundary condition at \(\infty\).”

For example, we could take our boundary condition at infinity to be that no incoming traveling waves appear on the string. Physically, this corresponds to the situtation in which the motion of the string at \(x = 0\) is producing the waves. In general, we can write a solution with angular frequency \(\omega\) as a sum of four real traveling waves \[\begin{aligned}
&\psi(x, t)=a \cos (k x-\omega t)+b \sin (k x-\omega t) \\
&+c \cos (k x+\omega t)+d \sin (k x+\omega t) .
\end{aligned}\]

Then (9.1) implies \[a+c=A, \quad b-d=0 ,\]

and the boundary condition at \(\infty\) implies \[c=d=0 .\]

Thus \[\psi(x, t)=A \cos (k x-\omega t) .\]

Infinite Systems

Now consider two semi-infinite strings with the same tension but different densities that are tied together at \(x = 0\), as shown in Figure \( 9.1\). Suppose that in the \(x \leq 0\) region (Region \(I\)), there is an incoming traveling wave with amplitude \(A\) and angular frequency \(\omega\), and in the \(x \geq 0\) region (Region \(II\)), there is no incoming traveling wave. This describes a physical situation in which the incoming wave in \(I\) is scattered by the boundary so that the other waves are a transmitted wave in \(II\) and a reflected wave in \(I\), both outgoing.

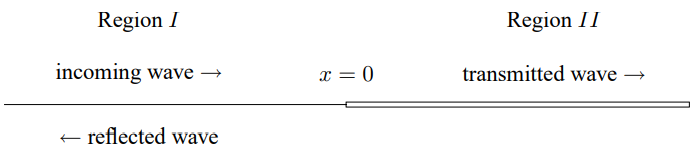
Figure \( 9.1\): Two semi-infinite strings tied together at \(x = 0\).

The key to this problem is to think of it as a forced oscillation problem. The incoming traveling wave in region \(I\) is what is “causing” all the oscillations. We have put the word in quotes, because the harmonic form, \(e^{-i \omega t}\), for the oscillation implies that it has been going on forever, so that a philosopher might question this use of cause and effect. Nevertheless, it will help us to think of it this way. If the reflected and transmitted waves are produced by the incoming wave, their amplitudes will also be proportional to \(e^{-i \omega t}\). As in a conventional forced oscillation problem, we could add on any free oscillations of the system. However, if there is any friction at all, these will die away with time, and we will be left only with the oscillation produced by the incoming traveling wave, proportional to \(e^{-i \omega t}\). The important thing is that the frequency is the same in both regions, because as in a forced oscillation problem, the frequency is imposed on the system by an external agency, in this case, whatever produced the incoming traveling wave.

In our complex exponential notation in which everything has the irreducible time dependence, \(e^{-i \omega t}\). Right moving waves are \(\propto e^{i k x} e^{-i \omega t}\) and left moving waves are \(\propto e^{-i k x} e^{-i \omega t}\). In this case, the boundary conditions at \(\pm \infty\) require that \[\psi(x, t)=e^{i k x} A e^{-i \omega t}+R A e^{-i k x} e^{-i \omega t}\]

for \(x \leq 0\) in Region \(I\), and \[\psi(x, t)=\tau A e^{i k^{\prime} x} e^{-i \omega t}\]

for \(x \geq 0\) in Region \(II\). The \(k\) and \(k^{\prime}\) are \[k=\omega \sqrt{\rho_{I} / T}, \quad k^{\prime}=\omega \sqrt{\rho_{I I} / T} ,\]

and \(R\) and \(\tau\) are (in general) complex numbers that determine the reflected and transmitted waves. They are sometimes called the “reflection coefficient” and “transmission coefficient,” or the “amplitudes” for transmission and reflection. Notice that we have defined the reflection and transmission coefficients by taking out a factor of the amplitude, \(A\), of the incoming wave. The amplitude, \(A\), then drops out of all the boundary conditions, and the dimensionless coefficients \(R\) and \(\tau\) are independent of \(A\). This must be so because of the linearity of the system. We know that once we have found the solution, \(\psi(x, t)\), for an incoming amplitude, \(A\), we can find the solution for an incoming amplitude, \(B\), by multiplying our solution by \(B / A\). We will keep the parameter, \(A\), in our expressions for \(\psi(x, t)\), mostly in order to keep the units right. \(A\) has units of length in this example, but in general, the amplitude of the incoming wave will have units of generalized displacement (as in (1.107) and (1.108)).

To determine \(R\) and \(\tau\), we need a boundary condition at \(x = 0\) where (9.6) and (9.7) meet. Clearly \(\psi(x, t)\) must be continuous at \(x = 0\), thus \[1+R=\tau .\]

We have canceled the common factor of \(A e^{-i \omega t}\) from both sides. The \(x\) derivative must also be continuous (for a massless knot) because the vertical forces on the knot must balance, thus \[i k(1-R)=i k^{\prime} \tau .\]

Solving for \(R\) and \(\tau\) gives \[\tau=\frac{2}{1+k^{\prime} / k}, \quad R=\frac{1-k^{\prime} / k}{1+k^{\prime} / k} .\]

Impedance Matching

Note that we could replace the string in Region \(II\) by a dashpot with the same impedance, \(Z_{II}\). This must be true because of the local nature of the interactions. The only thing that the string for \(x < 0\) knows about the string for \(x > 0\) is that it exerts a force at \(x = 0\) equal to \[-Z_{I I} \frac{\partial}{\partial t} \psi(0, t) .\]

Thus we also learned what happens when an incoming wave encounters a dashpot with the wrong impedance. The amplitude of the reflected wave is given by \(R\) in (9.11).

The reflected wave in (9.11) vanishes if \(k = k^{\prime}\). If \(k = k^{\prime}\), then \(\rho_{I} = \rho_{II}\) (from (9.8)), and the impedance in region \(I\) is the same as the impedance in region \(II\). This is a simple example of the important principle of “impedance matching.” There is no reflection if the impedance of the system in region \(II\) is the same as the impedance of the system in region \(I\). The argument is the same as for the dashpot in the previous paragraph. What matters in the computation of the reflection coefficient are the forces that act on the string at \(x = 0\). Those forces are determined by the impedances in the two regions. Nothing else matters. Consider, for example, the system shown in Figure \( 9.2\) of two semi-infinite strings connected at \(x = 0\) to a massless ring which is free to slide in the vertical direction on a frictionless rod. The rod can exert a horizontal force on the ring, so the tensions in the two strings need not be the same. In such a system, we can change both the density and the tension in the string from region \(I\) to region \(II\). There will be no reflection so long as the product of the linear mass density and the tension (and thus the impedance, from (8.22)) is the same in both regions, \[Z_{I}=\sqrt{\rho_{I} T_{I}}=\sqrt{\rho_{I I} T_{I I}}=Z_{I I} .\]

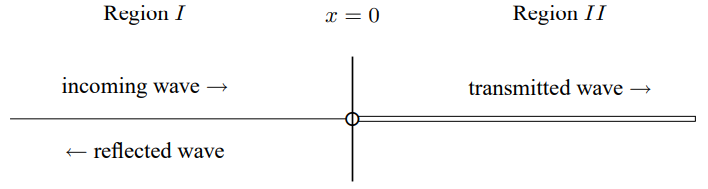
Figure \( 9.2\): A system in which impedances can be matched.

It is instructive to solve the scattering problem completely for the more general case shown in Figure \( 9.2\). This will give us a feeling for the meaning of impedance. The form of the solution, (9.6) and (9.7) is unchanged, but now the angular wave numbers satisfy \[k=\omega \sqrt{\rho_{I} / T_{I}}, \quad k^{\prime}=\omega \sqrt{\rho_{I I} / T_{I I}} .\]

The boundary condition at \(x = 0\) arising from the continuity of the string, (9.9), remains unchanged. However, (9.10) arose from the fact that the forces on the massless knot must sum to zero so the acceleration is not infinite. In this case, from (8.21), the contribution of each component of the wave to the total force is proportional to plus or minus the impedance in the relevant region depending on whether it is moving in the \(+ x\) or the \(- x\) direction. Thus the boundary condition is \[Z_{I}(1-R)=Z_{I I} \tau .\]

Then the reflection and transmission coefficients are \[\tau=\frac{2 Z_{I}}{Z_{I}+Z_{I I}}, \quad R=\frac{Z_{I}-Z_{I I}}{Z_{I}+Z_{I I}} .\]

We have already discussed the case where the impedances match and the reflection coefficient vanishes. It is also interesting to look at the limits in which \(R=\pm 1\). First consider the limit in which the impedance in region \(II\) goes to infinity, \[\lim _{Z_{I I} \rightarrow \infty} R=-1 .\]

This is situation in which it takes an infinite force to produce a wave in region \(II\). Thus the string in region \(II\) does not move at all, and in particular, the point \(x = 0\) might as well be a fixed end. The solution, (9.17) ensures that the string does not move at \(x = 0\), and therefore that the solution in region \(I\) is \(\psi(x, t) \propto \sin k x\). This solution is an infinite standing wave with a fixed end boundary condition.

In the opposite limit, in which the impedance in region \(II\) is zero, we get \[\lim _{Z_{I I} \rightarrow 0} R=1 .\]

This time, it takes no force at all to produce a wave in region \(II\). Thus the end of region \(I\) at \(x = 0\) feels no transverse force. It acts like a free end. The solution, (9.18) ensures that \(\psi(x, t) \propto \cos k x\) in region \(I\), so the slope of the string vanishes at \(x = 0\). This solution is an infinite standing wave with a free end boundary condition.

Looking at Reflected Waves

9-1
In this section, we discuss what the displacement in Region I looks like. We will find a useful diagnostic for the presence of reflection. We will also conclude that standing waves are very special.

Look at a wave of the form \[A \cos (k x-\omega t)+R A \cos (k x+\omega t) .\]

This describes an incoming traveling wave with some reflected wave of amplitude \(R\) (we could put in an arbitrary phase for the reflected wave but it would complicate the algebra without changing the physics).

For \(R=\pm 1\), this is a standing wave. For \(R = 0\), it is a traveling wave. To see how the system interpolates between these two extremes, consider the motion of the crest of the wave, a maximum of (9.19).

To find the maximum, we differentiate with respect to \(x\) and set the result to zero. Eliminating the irrelevant factor of \(A\), we get \[\sin (k x-\omega t)+R \sin (k x+\omega t)=0 ,\]

or \[(1+R) \sin k x \cos \omega t=(1-R) \cos k x \sin \omega t ,\]

or \[\tan k x=\frac{1-R}{1+R} \tan \omega t .\]

(9.22) describes (implicitly — we could solve for \(x\) as a function of \(t\) if we felt like it) the motion of the maximum as a function of time. We can differentiate it to get the velocity: \[k\left(1+\tan ^{2} k x\right) \frac{\partial x}{\partial t}=\frac{1-R}{1+R} \frac{\omega}{\cos ^{2} \omega t} .\]

We have left \(\left(1+\tan ^{2} k x\right)\) in (9.23) so that we can eliminate it by using (9.22). Thus \[\begin{aligned}
& \frac{\partial x}{\partial t}=\frac{1-R}{1+R} \frac{\omega}{k} \frac{1}{\left(1+\tan ^{2} k x\right) \cos ^{2} \omega t} \\
=& \frac{1-R}{1+R} \frac{\omega}{k} \frac{1}{\left(1+\left(\frac{1-R}{1+R}\right)^{2} \tan ^{2} \omega t\right) \cos ^{2} \omega t} \\
=& v \frac{(1+R)(1-R)}{(1+R)^{2} \cos ^{2} \omega t+(1-R)^{2} \sin ^{2} \omega t}
\end{aligned}\]

where \(v=\omega / k\) is the phase velocity. When \(\sin \omega t\) vanishes, the speed of the maximum is smaller than the phase velocity by a factor of \[\frac{1-R}{1+R} ,\]

while when \(\cos \omega t\) vanishes, the speed is larger than the \(v\) by the inverse factor, \[\frac{1+R}{1-R} .\]

The wave thus appears to move in fits and starts. You can easily see this effect if you stare at a system with a lot of reflection. The effect is illustrated in program 9-1.

We can draw a more general moral from this discussion. The general case of wave motion is much more like a traveling wave than like a standing wave. Generically, except for \(R=\pm 1\), the wave crests move with time. As we approach \(R=\pm 1\), one of the two velocities in (9.25) and (9.26) goes to zero and the other goes to infinity. What happens when you are close to \(R=\pm 1\) is then that the wave stays nearly still most of the time, and then moves very quickly to the next nearly stationary position. A standing wave is thus a degenerate special case of a traveling wave in which this motion is unobservable because, in a sense, it is infinitely fast.

Power and Reflection

It is instructive to consider the power required to produce a traveling wave that is partially reflected. That is, we consider the power required by a transverse force acting at \(x = 0\) to produce a wave in the region \(x > 0\) that is a linear combination of an outgoing wave moving in the \(+ x\) direction and an incoming wave moving in the \(- x\) direction, such as might be produced by a reflection at some large value of \(x\). Let us imagine the most general one-dimensional case, in a medium with impedance Z: \[\begin{gathered}
\psi(x, t)=\operatorname{Re}\left(A_{+} e^{i(k x-\omega t)}+A_{-} e^{i(-k x-\omega t)}\right) \\
=R_{+} \cos \left(k x-\omega t+\phi_{+}\right)+R_{-} \cos \left(-k x-\omega t+\phi_{-}\right)
\end{gathered}\]

where \(R_{\pm}\) and \(\phi_{\pm}\) are the absolute value and phase of the amplitude \(A_{\pm}\). The velocity is \[\frac{\partial}{\partial t} \psi(x, t)=\omega R_{+} \sin \left(k x-\omega t+\phi_{+}\right)+\omega R_{-} \sin \left(-k x-\omega t+\phi_{-}\right) .\]

Now because (9.27) involves waves traveling both in the \(+ x\) and in the \(- x\) direction, we cannot find the force required to produce the wave at the point \(x\) by simply multiplying (9.28) by the impedance, \(Z\). However, we can use linearity. We can write \(\psi(x, t)=\psi_{+}(x, t)+\psi_{-}(x, t)\), where \(\psi_{\pm}(x, t)\) is the wave moving in the \(\pm x\) direction. Then from (8.21), the force required to produce \(\psi_{+}\) is \[F_{+}(t)=Z \frac{\partial}{\partial t} \psi_{+}(0, t)\]

while the force required to produce \(\psi_{-}\) is \[F_{-}(t)=-Z \frac{\partial}{\partial t} \psi_{-}(0, t) .\]

Then the total force required to produce \(\psi\) is \[\begin{gathered}
F(t)=F_{+}(t)+F_{-}(t) \\
=Z \omega R_{+} \sin \left(-\omega t+\phi_{+}\right)-Z \omega R_{-} \sin \left(-\omega t+\phi_{-}\right) .
\end{gathered}\]

Thus the power required is \[\begin{gathered}
P(t)=\left.F(t) \frac{\partial}{\partial t} \psi(x, t)\right|_{x=0} \\
=Z \omega^{2} R_{+}^{2} \sin ^{2}\left(-\omega t+\phi_{+}\right)-Z \omega^{2} R_{-}^{2} \sin ^{2}\left(-\omega t+\phi_{-}\right) .
\end{gathered}\]

The average power is then given by \[P_{\text {average }}=\frac{1}{2} Z \omega^{2}\left(R_{+}^{2}-R_{-}^{2}\right)=\frac{1}{2} Z \omega^{2}\left(\left|A_{+}\right|^{2}-\left|A_{-}\right|^{2}\right) .\]

The result, (9.32), has an obvious and important physical interpretation. Positive power is required to produce the outgoing traveling wave, while the incoming wave gives energy back to the system, and thus requires negative power. The power required to produce a general traveling wave is thus proportional to the difference of the squares of the absolute values of the amplitudes of the outgoing and incoming waves.

Note also that we can apply this discussion to the example of reflection at a boundary, discussed above. We can check that energy is conserved in this scattering. The average power required to produce the wave in region \(I\) is, from (9.33) \[Z_{I} \omega^{2}-Z_{I} \omega^{2} R^{2} .\]

The average power required to produce the wave in region \(II\) is, \[Z_{I I} \omega^{2} \tau^{2} .\]

Using (9.16), you can check that these are equal.

Mass on a String

9-2

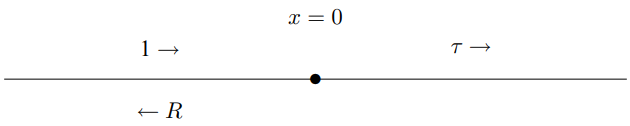
Figure \( 9.3\): A mass on a string.

Consider the transmission and reflection of waves from a mass, \(m\), at \(x = 0\) on a string with linear mass density \(\rho\) and tension \(T\), stretched from \(x=-\infty\) to \(x=\infty\), shown in Figure \( 9.3\). Before we calculate the coefficients for reflection and transmission, let us guess the result in two extreme limits.

\(m\) small – Here we expect that the reflection to be small and the transmission close to one, because in the limit \[m \rightarrow 0 \Rightarrow \tau \rightarrow 1 \text { and } R \rightarrow 0 .\]

\(m\) large – Here we expect the transmission to be small and the reflection close to \(- 1\), because in the limit \[m \rightarrow \infty \rightarrow \tau \rightarrow 0 \text { and } R \rightarrow-1 .\]

“Large or small compared to what?” you ask! That we can answer by dimensional analysis. The relevant dimensional parameters are \(m\), \(\omega\), \(k\), \(\rho\) and \(T\). However, one of these is not independent, because of the dispersion relation, (6.5). If we use (6.5) to eliminate \(T\), then \(\omega\) cannot be relevant to the question, because it is the only thing left that involves the unit of time. The only dimensionless quantity we can build is \[\epsilon=\frac{m k}{\rho}=\frac{m \omega^{2}}{k T} .\]

Now that we have guessed, we can do the calculation. It follows from translation invariance and the boundary condition at \(x = \infty\) that \[\psi(x, t)=A e^{i k x} e^{-i \omega t}+R A e^{-i k x} e^{-i \omega t} \text { for } x \leq 0\]

\[\psi(x, t)=\tau A e^{i k x} e^{-i \omega t} \text { for } x \geq 0\]

where, as usual, \(R\) and \(\tau\) are “amplitudes” for the reflected and transmitted waves. The boundary conditions are

continuity – The fact that the string doesn’t break implies that it is continuous, so that \(\psi(0, t)\) can be computed with either (9.39) or (9.40). This implies \[1+R=\tau .\]

\(F = ma\) – The horizontal component of the tension in the string must be equal on the two sides. Both are about equal to \(T\), for small displacements. However, if there is a kink in the string, the vertical components do not match, as shown in Figure \( 9.4\) (see also (8.16)-(8.17)). The force on the mass is then the tension times the slope for \(x \geq 0\) minus the tension times the slope for \(x \leq 0\), thus \(F = ma\) becomes \[\begin{gathered}
T\left(\left.\frac{\partial}{\partial x} \psi(x, t)\right|_{x=0^{+}}-\left.\frac{\partial}{\partial x} \psi(x, t)\right|_{x=0^{-}}\right) \\
=m \frac{\partial^{2}}{\partial t^{2}} \psi(0, t)
\end{gathered}\]

or \[i k T(R-1+\tau)=-m \omega^{2} \tau .\]

Thus \[1+R=\tau, \quad 1-R=(1-i \epsilon) \tau ,\]

so that \[\tau=\frac{2}{2-i \epsilon}, \quad R=\frac{i \epsilon}{2-i \epsilon} .\]

Clearly, this is in accord with our guess.

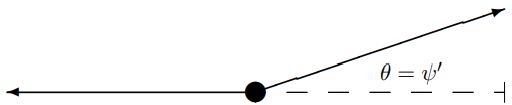
Figure \( 9.4\): The force on the mass.

Note that these amplitudes, unlike those in (9.11), are complex numbers. The transmitted and reflected waves do not have the same phase as the incoming wave at the boundary. The phase difference between the transmitted (or reflected) wave is called a “phase shift.” One interesting feature of the solution, (9.45), that we did not guess is that for large \(\epsilon\), the small transmitted wave is \(90^{\circ}\) out of phase with the incoming wave.

This scattering is animated in program 9-2. The solution is also decomposed into incoming, transmitted and reflected waves. Stare at the mass and see if you can understand how the kink in the string is related to its acceleration. You can also make the mass larger and smaller to approach the limits (9.36) and (9.37).