5.7: Wave-Particle Duality
- Last updated
- Oct 10, 2022
- Save as PDF
- Page ID
- 64342
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Identify phenomena in which electromagnetic waves behave like a beam of photons and particles behave like waves
- Describe the physics principles behind electron microscopy
- Summarize the evolution of scientific thought that led to the development of quantum mechanics
The energy of radiation detected by a radio-signal receiving antenna comes as the energy of an electromagnetic wave. The same energy of radiation detected by a photocurrent in the photoelectric effect comes as the energy of individual photon particles. Therefore, the question arises about the nature of electromagnetic radiation: Is a photon a wave or is it a particle? Similar questions may be asked about other known forms of energy. For example, an electron that forms part of an electric current in a circuit behaves like a particle moving in unison with other electrons inside the conductor. The same electron behaves as a wave when it passes through a solid crystalline structure and forms a diffraction image. Is an electron a wave or is it a particle? The same question can be extended to all particles of matter—elementary particles, as well as compound molecules—asking about their true physical nature. At our present state of knowledge, such questions about the true nature of things do not have conclusive answers. All we can say is that wave-particle duality exists in nature: Under some experimental conditions, a particle appears to act as a particle, and under different experimental conditions, a particle appears to act a wave. Conversely, under some physical circumstances electromagnetic radiation acts as a wave, and under other physical circumstances, radiation acts as a beam of photons.
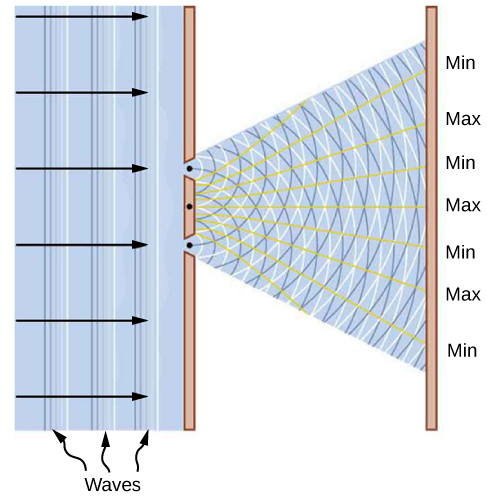
This dualistic interpretation is not a new physics concept brought about by specific discoveries in the twentieth century. It was already present in a debate between Isaac Newton and Christiaan Huygens about the nature of light, beginning in the year 1670. According to Newton, a beam of light is a collection of corpuscles of light. According to Huygens, light is a wave. The corpuscular hypothesis failed in 1803, when Thomas Young announced his double-slit interference experiment with light (see Figure 5.7.1), which firmly established light as a wave. In James Clerk Maxwell’s theory of electromagnetism (completed by the year 1873), light is an electromagnetic wave. Maxwell’s classical view of radiation as an electromagnetic wave is still valid today; however, it is unable to explain blackbody radiation and the photoelectric effect, where light acts as a beam of photons.
A similar dichotomy existed in the interpretation of electricity. From Benjamin Franklin’s observations of electricity in 1751 until J.J. Thomson’s discovery of the electron in 1897, electric current was seen as a flow in a continuous electric medium. Within this theory of electric fluid, the present theory of electric circuits was developed, and electromagnetism and electromagnetic induction were discovered. Thomson’s experiment showed that the unit of negative electric charge (an electron) can travel in a vacuum without any medium to carry the charge around, as in electric circuits. This discovery changed the way in which electricity is understood today and gave the electron its particle status. In Bohr’s early quantum theory of the hydrogen atom, both the electron and the proton are particles of matter. Likewise, in the Compton scattering of X-rays on electrons, the electron is a particle. On the other hand, in electron-scattering experiments on crystalline structures, the electron behaves as a wave.
A skeptic may raise a question that perhaps an electron might always be nothing more than a particle, and that the diffraction images obtained in electron-scattering experiments might be explained within some macroscopic model of a crystal and a macroscopic model of electrons coming at it like a rain of ping-pong balls. As a matter of fact, to investigate this question, we do not need a complex model of a crystal but just a couple of simple slits in a screen that is opaque to electrons. In other words, to gather convincing evidence about the nature of an electron, we need to repeat the Young double-slit experiment with electrons. If the electron is a wave, we should observe the formation of interference patterns typical for waves, such as those described in Figure 5.7.1, even when electrons come through the slits one by one. However, if the electron is a not a wave but a particle, the interference fringes will not be formed.
The very first double-slit experiment with a beam of electrons, performed by Claus Jönsson in Germany in 1961, demonstrated that a beam of electrons indeed forms an interference pattern, which means that electrons collectively behave as a wave. The first double-slit experiments with single electrons passing through the slits one-by-one were performed by Giulio Pozzi in 1974 in Italy and by Akira Tonomura in 1989 in Japan. They show that interference fringes are formed gradually, even when electrons pass through the slits individually. This demonstrates conclusively that electron-diffraction images are formed because of the wave nature of electrons. The results seen in double-slit experiments with electrons are illustrated by the images of the interference pattern in Figure 5.7.2.

Example 5.7.1: Double-Slit Experiment with Electrons
In one experimental setup for studying interference patterns of electron waves, two slits are created in a gold-coated silicon membrane. Each slit is 62-nm wide and 4-μm long, and the separation between the slits is 272 nm. The electron beam is created in an electron gun by heating a tungsten element and by accelerating the electrons across a 600-V potential. The beam is subsequently collimated using electromagnetic lenses, and the collimated beam of electrons is sent through the slits. Find the angular position of the first-order bright fringe on the viewing screen.
Strategy
Recall that the angular position θ of the nth order bright fringe that is formed in Young’s two-slit interference pattern (discussed in a previous chapter) is related to the separation, d, between the slits and to the wavelength, λ, of the incident light by the equation dsin θ = nλ, where n = 0, ±1, ±2,.... The separation is given and is equal to d = 272 nm. For the first-order fringe, we take n = 1. The only thing we now need is the wavelength of the incident electron wave.
Since the electron has been accelerated from rest across a potential difference of ΔV = 600 V, its kinetic energy is K = e ΔV = 600 eV. The rest-mass energy of the electron is E0 = 511 keV.
We compute its de Broglie wavelength as that of a nonrelativistic electron because its kinetic energy K is much smaller than its rest energy E0, K ≪ E0.
Solution
The electron’s wavelength is
λ=hp=h√2meK=h√2E0/c2K=hc√2E0K=1.241×10−6eV⋅m√2(511keV)(600eV)=0.050nm.
This λ is used to obtain the position of the first bright fringe:
sinθ=1⋅λd=0.050nm272nm=0.000184⇒θ=0.010°.
Significance
Notice that this is also the angular resolution between two consecutive bright fringes up to about n = 1000. For example, between the zero-order fringe and the first-order fringe, between the first-order fringe and the second-order
Exercise 5.7.1
For the situation described in Example 5.7.1, find the angular position of the fifth-order bright fringe on the viewing screen.
- Answer
-
0.052o
The wave-particle dual nature of matter particles and of radiation is a declaration of our inability to describe physical reality within one unified classical theory because separately neither a classical particle approach nor a classical wave approach can fully explain the observed phenomena. This limitation of the classical approach was realized by the year 1928, and a foundation for a new statistical theory, called quantum mechanics, was put in place by Bohr, Edwin Schrödinger, Werner Heisenberg, and Paul Dirac. Quantum mechanics takes de Broglie’s idea of matter waves to be the fundamental property of all particles and gives it a statistical interpretation. According to this interpretation, a wave that is associated with a particle carries information about the probable positions of the particle and about its other properties. A single particle is seen as a moving wave packet such as the one shown in Figure 5.7.3. We can intuitively sense from this example that if a particle is a wave packet, we will not be able to measure its exact position in the same sense as we cannot pinpoint a location of a wave packet in a vibrating guitar string. The uncertainty, Δx, in measuring the particle’s position is connected to the uncertainty, Δp, in the simultaneous measuring of its linear momentum by Heisenberg’s uncertainty principle:
ΔxΔp≥12ℏ.
Heisenberg’s principle expresses the law of nature that, at the quantum level, our perception is limited. For example, if we know the exact position of a body (which means that Δx = 0 in Equation ???) at the same time we cannot know its momentum, because then the uncertainty in its momentum becomes infinite (because Δp ≥ 0.5 ℏ/Δx in Equation ???). The Heisenberg uncertainty principle sets the limit on the precision of simultaneous measurements of position and momentum of a particle; it shows that the best precision we can obtain is when we have an equals sign (=) in Equation ???, and we cannot do better than that, even with the best instruments of the future. Heisenberg’s principle is a consequence of the wave nature of particles.

We routinely use many electronic devices that exploit wave-particle duality without even realizing the sophistication of the physics underlying their operation. One example of a technology based on the particle properties of photons and electrons is a charge-coupled device, which is used for light detection in any instrumentation where high-quality digital data are required, such as in digital cameras or in medical sensors. An example in which the wave properties of electrons is exploited is an electron microscope.
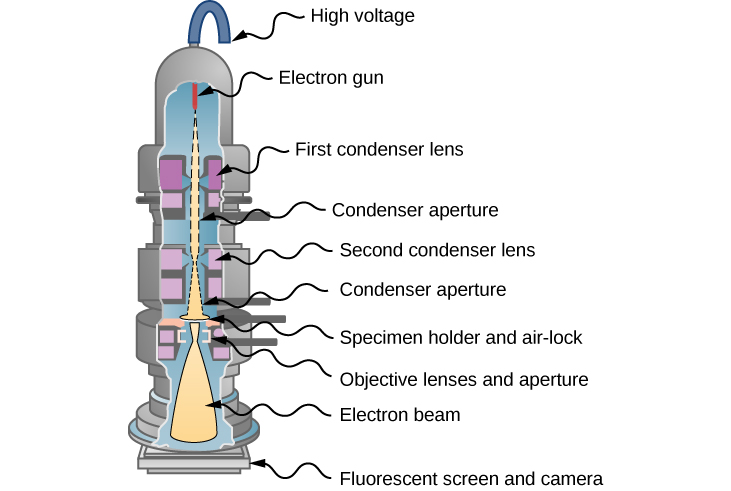
In 1931, physicist Ernst Ruska - building on the idea that magnetic fields can direct an electron beam just as lenses can direct a beam of light in an optical microscope—developed the first prototype of the electron microscope. This development originated the field of electron microscopy. In the transmission electron microscope (TEM), shown in Figure 5.7.4, electrons are produced by a hot tungsten element and accelerated by a potential difference in an electron gun, which gives them up to 400 keV in kinetic energy. After leaving the electron gun, the electron beam is focused by electromagnetic lenses (a system of condensing lenses) and transmitted through a specimen sample to be viewed. The image of the sample is reconstructed from the transmitted electron beam. The magnified image may be viewed either directly on a fluorescent screen or indirectly by sending it, for example, to a digital camera or a computer monitor. The entire setup consisting of the electron gun, the lenses, the specimen, and the fluorescent screen are enclosed in a vacuum chamber to prevent the energy loss from the beam. Resolution of the TEM is limited only by spherical aberration (discussed in a previous chapter). Modern high-resolution models of a TEM can have resolving power greater than 0.5 Å and magnifications higher than 50 million times. For comparison, the best resolving power obtained with light microscopy is currently about 97 nm. A limitation of the TEM is that the samples must be about 100-nm thick and biological samples require a special preparation involving chemical “fixing” to stabilize them for ultrathin slicing.
Such limitations do not appear in the scanning electron microscope (SEM), which was invented by Manfred von Ardenne in 1937. In an SEM, a typical energy of the electron beam is up to 40 keV and the beam is not transmitted through a sample but is scattered off its surface. Surface topography of the sample is reconstructed by analyzing back-scattered electrons, transmitted electrons, and the emitted radiation produced by electrons interacting with atoms in the sample. The resolving power of an SEM is better than 1 nm, and the magnification can be more than 250 times better than that obtained with a light microscope. The samples scanned by an SEM can be as large as several centimeters but they must be specially prepared, depending on electrical properties of the sample.
High magnifications of the TEM and SEM allow us to see individual molecules. High resolving powers of the TEM and SEM allow us to see fine details, such as those shown in the SEM micrograph of pollen at the beginning of this chapter (Figure 6.1.1).
Example 5.7.2: Resolving Power of an Electron Microscope
If a 1.0-pm electron beam of a TEM passes through a 2.0-μm circular opening, what is the angle between the two just-resolvable point sources for this microscope?
Solution
We can directly use a formula for the resolving power, Δθ, of a microscope when the wavelength of the incident radiation is λ=1.0pm and the diameter of the aperture is D=2.0μm:
Δθ=1.22λD=1.221.0pm2.0μm=6.10×10−7rad=3.50×10.5o.
Significance
Note that if we used a conventional microscope with a 400-nm light, the resolving power would be only 14°, which means that all of the fine details in the image would be blurred.
Exercise 5.7.2
Suppose that the diameter of the aperture in Example 5.7.2 is halved. How does it affect the resolving power?
- Answer
-
doubles it


