13.3.1: Transverse Waves
- Page ID
- 97360
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Transverse Waves
A familiar example of a transverse wave occurs when you toss a rock into a lake or pond. When the rock hits the surface of the water, ripples are produced. The ripples are formed by the energy of the falling rock being shared by the water molecules near the impact point. As those molecules transfer the energy to molecules located further away, the ripples expand outward from the impact point. Although the energy spreads out horizontally through the water, the water molecules do not move horizontally. As the energy is transferred from one water molecule to the next, the surface of the water bounces up and down, each molecule acting like a simple harmonic oscillator.
A way to help visualize the difference between the wave speed and the speed of the water molecules is to imagine a line of people standing side by side. The person (water molecule) on the far left end is handed a ball (energy), and they pass the ball to the next person in line. Each person passes the ball to the next person until the ball has traveled from one end of the line to the other. None of the people move very much. They might lean to the left to receive the ball and then lean to the right to pass it to their neighbor, but they do not run with the ball. The ball definitely travels along the line with an average velocity, and even though each person leans left and right they do not change position, which gives them an average velocity of zero.
"Stones-Pebbles-Water" by geralt via Pixabay under CCO
Imagine a ripple moving through the water. Ahead of the ripple, the water is flat and undisturbed. There, the water surface is in a state of equilibrium. As the energy passes through the water, it produces a series of crests and troughs. The crests and troughs are created by the water surface rising and falling in a simple harmonic oscillation. If you took a picture of the water surface as the energy passes through, it would look something like this:
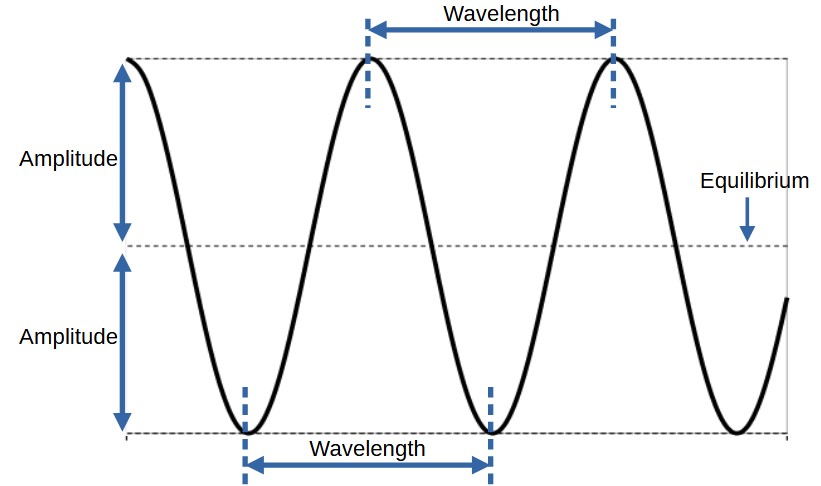
Parts of a wave, by Claude Mona, under CC BY NC
In a transverse wave, the atoms of the medium move perpendicular to the direction that the energy is moving through the medium. When the wave has passed, the atoms of the medium have returned to their equilibrium positions. All transverse waves share certain characteristics.
- Waves have an amplitude (A). The amplitude is how far from equilibrium the atoms of the material have moved as the wave energy passes through the system. The 'height' of the crests is the same as the 'depth' of the troughs.
- Waves have a wavelength \(( \lambda\)). The wavelength is set by how far the energy travels in one period. The wavelength is different from the amplitude. The wavelength measures the distance between two successive crests (or troughs) as the wave travels through the medium.
- Waves have a velocity (vwave). The wave velocity is a measure of how long it takes for the energy to pass from one atom to another. This is different than the velocity of the moving atoms.
The distance between two crests is defined to be the wavelength. We know that the time between two maximum amplitude positions in a simple harmonic system is defined to be the period. The energy traveled a distance \( \lambda\) in a time T. The ratio of displacement over time is the definition of velocity, so the wave speed is defined as vwave =\(\frac{\lambda}{\text{T}} \). Since period and frequency are related then vwave = \( \lambda\) f. This is true for all simple harmonic waves.
Another example of a transverse wave can be seen when two people hold the ends of a rope and one person rapidly wiggles their end of the rope up and down. A series of 'bumps' is produced and these 'bumps' travel along the rope, away from the wiggling end. Although the energy is moving horizontally along the rope, the rope is not moving horizontally. Instead, the rope travels up and down, with each section of the rope acting as a simple harmonic oscillator. Because of this, there is a wave speed which describes how quickly the 'bumps' move horizontally along the rope, but there is also the 'rope speed' which talks about how quickly the end of the rope is moving up and down.
A certain transverse wave has a wave velocity of 1580 meters per second. If the wavelength is 1.35 meters, what is the frequency of the wave?
Solution
Starting with vwave = \( \lambda\) f, you can solve for f = \(\frac{v_{\text{wave}}}{\lambda} \) = \(\frac{1580 \, \text{meters/second}}{1.35 \, \text{meters}} \) = 1170.4 Hertz.