16.6: Direct Calculation of Electrical Quantities from Charge Distributions (Exercises)
- Page ID
- 100312
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Conceptual Questions
Electric Dipoles
36. What are the stable orientation(s) for a dipole in an external electric field? What happens if the dipole is slightly perturbed from these orientations?
Calculating Electric Potential of Charge Distributions
13. Compare the electric dipole moments of charges \(\displaystyle ±Q\) separated by a distance d and charges \(\displaystyle ±Q/2\) separated by a distance d/2.
15. In what region of space is the potential due to a uniformly charged sphere the same as that of a point charge? In what region does it differ from that of a point charge?
16. Can the potential of a nonuniformly charged sphere be the same as that of a point charge? Explain.
Problems
Electric Dipoles
105. Consider the equal and opposite charges shown below. (a) Show that at all points on the x-axis for which \(\displaystyle |x|≫a,E≈Qa/2πε_0x^3\). (b) Show that at all points on the y-axis for which \(\displaystyle |y|≫a,E≈Qa/πε_0y^3\).
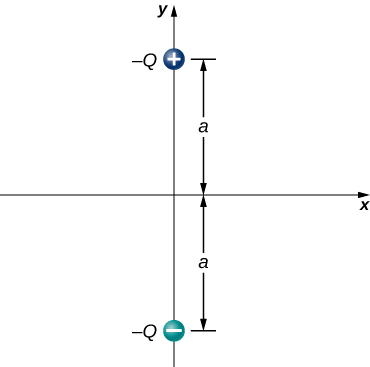
106. (a) What is the dipole moment of the configuration shown above? If Q=4.0μC,
(b) what is the torque on this dipole with an electric field of \(\displaystyle 4.0×10^5N/C\hat{i}\)?
(c) What is the torque on this dipole with an electric field of \(\displaystyle −4.0×10^5N/C\hat{i}\)?
(d) What is the torque on this dipole with an electric field of \(\displaystyle ±4.0×10^5N/C\hat{j}\)?
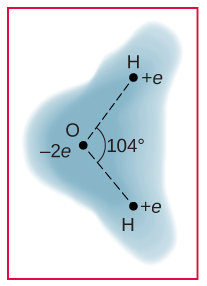
107. A water molecule consists of two hydrogen atoms bonded with one oxygen atom. The bond angle between the two hydrogen atoms is 104° (see below). Calculate the net dipole moment of a hypothetical water molecule where the charge at the oxygen molecule is −2e and at each hydrogen atom is +e. The net dipole moment of the molecule is the vector sum of the individual dipole moment between the two O-Hs. The separation O-H is 0.9578 angstroms.
Calculating Electric Fields of Charge Distributions
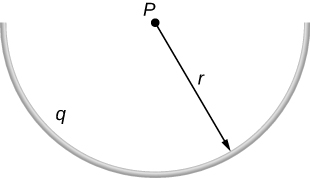
83. The charge per unit length on the thin rod shown below is \(\displaystyle λ\). What is the electric field at the point P? (Hint: Solve this problem by first considering the electric field \(\displaystyle d\vec{E}\) at P due to a small segment dx of the rod, which contains charge \(\displaystyle dq=λdx\). Then find the net field by integrating \(\displaystyle d\vec{E}\) over the length of the rod.)
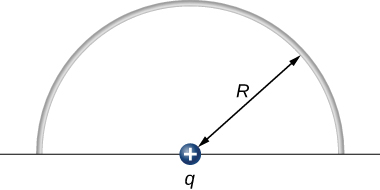
84. The charge per unit length on the thin semicircular wire shown below is λ. What is the electric field at the point P?
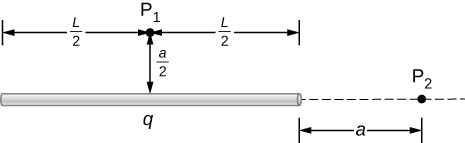
87. A total charge q is distributed uniformly along a thin, straight rod of length L (see below). What is the electric field at \(\displaystyle P_1\)? At \(\displaystyle P_2\)?
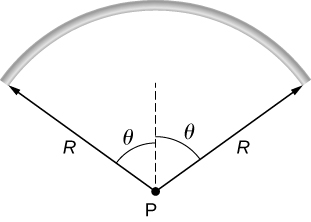
90. A rod bent into the arc of a circle subtends an angle \(\displaystyle 2θ\) at the center P of the circle (see below). If the rod is charged uniformly with a total charge Q, what is the electric field at P?.
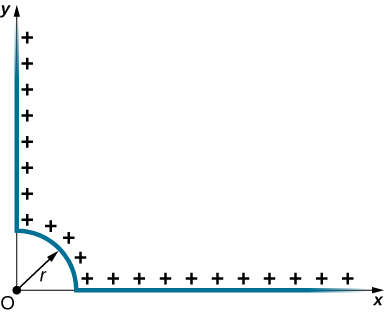
97. Positive charge is distributed with a uniform density \(\displaystyle λ\) along the positive x-axis from \(\displaystyle r\) to \(\displaystyle ∞\), along the positive y-axis from \(\displaystyle r\) to \(\displaystyle ∞\), and along a 90° arc of a circle of radius r, as shown below. What is the electric field at O?
121. Charge is distributed uniformly along the entire y-axis with a density \(\displaystyle y_λ\) and along the positive x-axis from \(\displaystyle x=a\) to \(\displaystyle x=b\) with a density \(\displaystyle λ_x\). What is the force between the two distributions?
122. The circular arc shown below carries a charge per unit length \(\displaystyle λ=λ_0cosθ\), where \(\displaystyle θ\) is measured from the x-axis. What is the electric field at the origin?
123. Calculate the electric field due to a uniformly charged rod of length L, aligned with the x-axis with one end at the origin; at a point P on the z-axis.
124. The charge per unit length on the thin rod shown below is \(\displaystyle λ\). What is the electric force on the point charge q? Solve this problem by first considering the electric force \(\displaystyle d\vec{F}\) on q due to a small segment \(\displaystyle dx\) of the rod, which contains charge \(\displaystyle λdx.\) Then, find the net force by integrating \(\displaystyle d\vec{F}\) over the length of the rod.
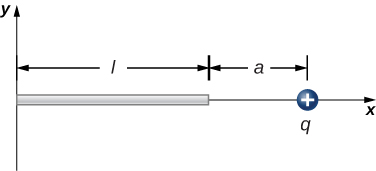
125. The charge per unit length on the thin rod shown here is \(\displaystyle λ\). What is the electric force on the point charge q? (See the preceding problem.)
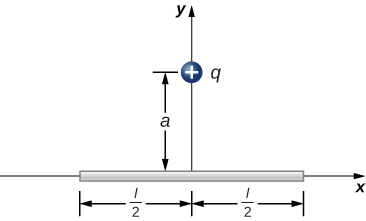
126. The charge per unit length on the thin semicircular wire shown below is \(\displaystyle λ\). What is the electric force on the point charge q? (See the preceding problems.)
