10.5: Fluids in Motion
- Last updated
- Jan 14, 2019
- Save as PDF
- Page ID
- 16996

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Determine the flow rate based on velocity and area or elapsed time and justify the use of continuity in expressing properties of a fluid and its motion
The flow rate of a fluid is the volume of fluid which passes through a surface in a given unit of time. It is usually represented by the symbol Q.
Continuity Equation for Fluids: A brief introduction to the Continuity Equation for Fluids.
Flow Rate
Volumetric flow rate is defined as
Q=v×a,
where Q is the flow rate, v is the velocity of the fluid, and a is the area of the cross section of the space the fluid is moving through. Volumetric flow rate can also be found with
Q=Vt
where Q is the flow rate, V is the Volume of fluid, and t is elapsed time.
Continuity
The equation of continuity works under the assumption that the flow in will equal the flow out. This can be useful to solve for many properties of the fluid and its motion:
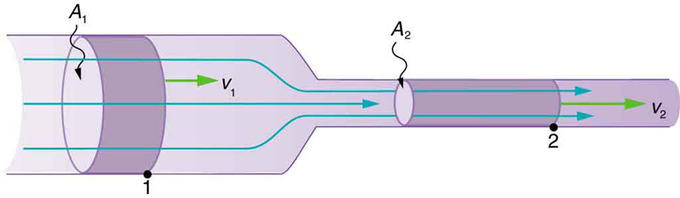
Flow in = Flow out: Using the known properties of a fluid in one condition, we can use the continuity equation to solve for the properties of the same fluid under other conditions.
Q1=Q2
This can be expressed in many ways, for example: A1v1=A2v2. The equation of continuity applies to any incompressible fluid. Since the fluid cannot be compressed, the amount of fluid which flows into a surface must equal the amount flowing out of the surface.
Applying the Continuity Equation
You can observe the continuity equation’s effect in a garden hose. The water flows through the hose and when it reaches the narrower nozzle, the velocity of the water increases. Speed increases when cross-sectional area decreases, and speed decreases when cross-sectional area increases. This is a consequence of the continuity equation. If the flow Q is held constant, when the area A decreases, the velocity v must increase proportionally. For example, if the nozzle of the hose is half the area of the hose, the velocity must double to maintain the continuous flow.
Key Points
- Flow rate can be expressed in either terms of cross sectional area and velocity, or volume and time.
- Because liquids are incompressible, the rate of flow into an area must equal the rate of flow out of an area. This is known as the equation of continuity.
- The equation of continuity can show how much the speed of a liquid increases if it is forced to flow through a smaller area. For example, if the area of a pipe is halved, the velocity of the fluid will double.
- Although gases often behave as fluids, they are not incompressible the way liquids are and so the continuity equation does not apply.
Key Terms
- incompressible: Unable to be compressed or condensed.
- continuity: Lack of interruption or disconnection; the quality of being continuous in space or time.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Equation of continuity. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Equation_of_continuity. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Flow Rate and Its Relation to Velocity. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42205/latest/. License: CC BY: Attribution
- Bernoulli's equation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Bernoulli's_equation. License: CC BY-SA: Attribution-ShareAlike
- Flow rate. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Flow_rate. License: CC BY-SA: Attribution-ShareAlike
- incompressible. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/incompressible. License: CC BY-SA: Attribution-ShareAlike
- continuity. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/continuity. License: CC BY-SA: Attribution-ShareAlike
- Continuity Equation for Fluids. Located at: http://www.youtube.com/watch?v=fR368Ps-xBI. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Flow Rate and Its Relation to Velocity. February 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42205/latest/. License: CC BY: Attribution


