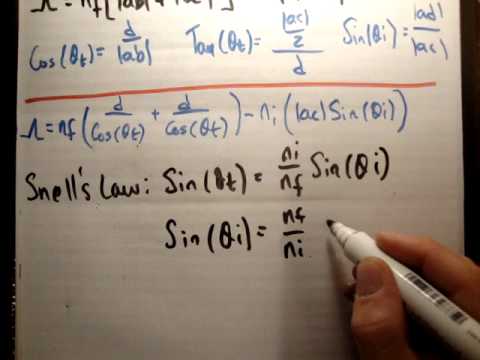6.3: Further Topics
- Last updated
- Jan 15, 2019
- Save as PDF
- Page ID
- 17120
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Describe process that leads to the thin film interference
Thin Film Interference
This is a phenomenon that occurs when incident rays reflected by the upper and lower boundaries of a thin film interfere with one another and form a new wave. A material is considered to be a thin film if its thickness is in the sub-nanometer to micron range, e.g. a soap bubble. Studying the new wave can shed light on properties of the film, such as thickness or refractive index. Interference effects are most prominent when the light interacts with something that has a size similar to its own wavelength. The thickness of a thin film is a few times smaller than the wavelength of the light, λ. Color is indirectly associated with wavelength. The interference ratio of wavelength to size of the object causes the appearance of colors.
Thin Film Interference: In this video I continue with my tutorials on Electromagnetism to Optics which is pitched at university undergraduate level. I have intended for a long time to record videos which describe the transition made from classical electromagnetism to optics. In many respects these videos will cover ‘wave’ optics. I devote much time to discussing the complex exponential representation of waves, Maxwell’s Equations, the wave equation etc.Specifically here, I derive the formula for the optical path difference and the phase difference for a ‘wave’ of light propagating through a thin film. This expression can be used for anti reflective coatings. The phase difference is the product of the optical path differene and the wave vector k.I hope it’s of use!! Thank you for watching and I hope that this matches your requirements.

Thin Film Interference in Oil: Thin film interference can be seen in this oil slick.
Examples of Thin Film Interference
You have probably witnessed thin film interference in your every day life and just not realized it. Whenever you see the bright, rainbow like colors in oil floating in water, shown in, this is thin film interference. The colors that appear in bubbles that kids play with are also a result of thin film interference. Thin film interference can have commercial applications, such as anti- reflection coatings and optical filters.
How it Works
shows a diagram of how thin film interference works. As light strikes the surface of a film it is either transmitted or reflected at the upper surface. Light that is transmitted reaches the bottom surface and may once again be transmitted or reflected. The light reflected from the upper and lower surfaces will interfere. The degree of constructive or destructive interference between the two light waves is dependent upon the difference in their phase. This difference is dependent upon the thickness of the film layer, the refractive index of the film, and the angle of incidence of the original wave on the film. Additionally, a phase shift of 180° or ππ radians may be introduced upon reflection at a boundary depending on the refractive indices of the materials on either side said boundary. This phase shift occurs if the refractive index of the medium the light is travelling through is less than the refractive index of the material it is striking. In other words, if n1<n2n1<n2and the light is travelling from material 1 to material 2, then a phase shift will occur upon reflection. The pattern of light that results from this interference can appear either as light and dark bands or as colorful bands depending upon the source of the incident light.
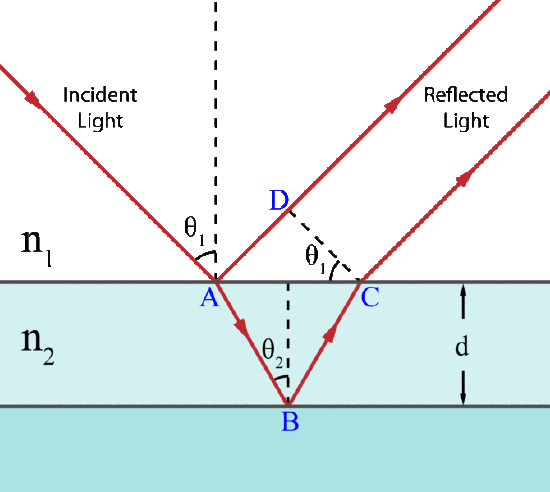
Light on a Thin Film: Light incident on a thin film. Demonstration of the optical path length difference for light reflected from the upper and lower boundaries.
Interference will be constructive if the optical path difference is equal to an integer multiple of the wavelength of light:
2n2dcos(θ2)=mλ
where mm is the integer, dd is the thickness of the film, and λλ is the wavelength of light. However, this condition may change if phase shifts occur upon reflection.
Polarization By Passing Light Through Polarizers
Polarization is the attribute that wave oscillations have a definite direction relative to the direction of propagation of the wave.
learning objectives
- Discuss polarization of electromagnetic waves
Definition of Polarization
As we discusses in previous atoms, light waves are a type of electromagnetic waves, in the visible spectrum. These electromagnetic (EM) waves are transverse waves. Figure 1 demonstrates that a transverse wave is one oscillates perpendicular to the direction of the energy transfer. If the wave is traveling from left to right, it is oscillating up and down. Polarization is the property of waves that allow them to oscillate in more than one direction, but that direction is relative to that of the direction the wave is traveling in. For an EM wave, the direction of polarization is the direction parallel to the electric field. In Figure 2 you can see that the EM and magnetic fields are perpendicular to the path of travel. Since the direction of polarization is parallel to the electric field, you can consider the blue arrows to be the direction of polarization.
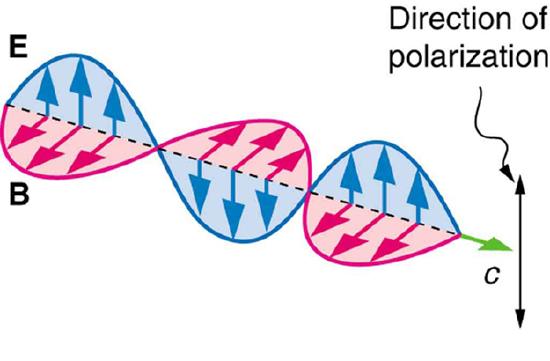
Figure 2: An EM wave, such as light, is a transverse wave. The electric and magnetic fields are perpendicular to the direction of propagation.
Figure 1: Transverse Waves
How it Works
Now, to examine the effects of passing light through a polarizer, lets look at Figure 3. shows a stationary vertical slot, which will act as a polarizer, and two waves traveling in the same direction, but one is oscillating vertically,a, (and therefore vertically polarized), and the other, b, horizontally. What happens to these waves as they pass through the polarizer?When wave a, the vertically oscillating wave is passed through the vertically polarized slot, nothing happens. The wave passes through untouched or manipulated. When wave b, the horizontally oscillating wave is passed through, the vertically polarized slot blocks the wave, and it is not passed through at all. Now that we understand the concept of polarization, and how it works, how can we apply this to make it useful? Look at Figure 4. The image on the left is full of glare, which makes it hard to see what we are looking at. The image on the right was taken with a polarized lens, so you only see the image, and none of the annoying glare. How this works is diagramed in Figure 5. Many light sources are unpolarized, and are comprised of many waves in all possible directions. Polarized lenses only allow one direction of light to pass through, minimizing the unwanted aspects of the light rays, such as glare. Simply, passing light through a polarized material changes the intensity of the light.
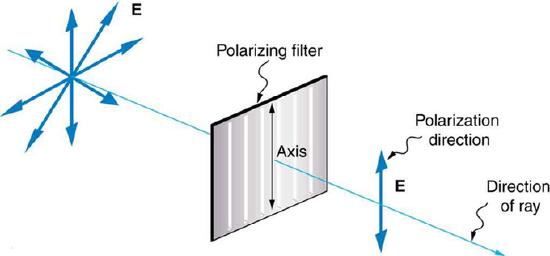
Figure 5: A polarizing filter has a polarization axis that acts as a slit passing through electric fields parallel to its direction. The direction of polarization of an EM wave is defined to be the direction of its electric field.

Figure 4: These two photographs of a river show the effect of a polarizing filter in reducing glare in light reflected from the surface of water. Part (b) of this figure was taken with a polarizing filter and part (a) was not. As a result, the reflection of clouds and sky observed in part (a) is not observed in part (b). Polarizing sunglasses are particularly useful on snow and water. (credit: Amithshs, Wikimedia Commons)
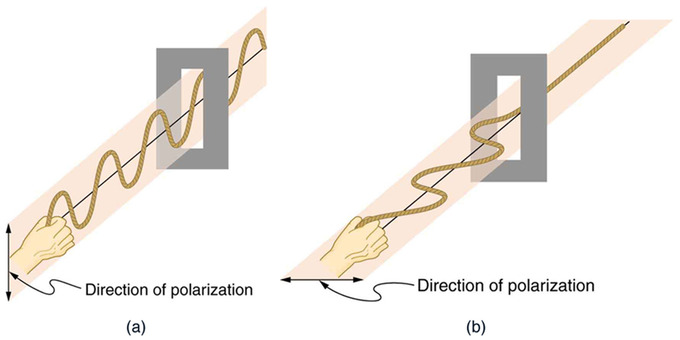
Figure 3: Example of passing light through a polarizer
Intensity
Lets call the angle between the direction of polarization and the axis of the polarization filter θ. The original intensity of the light before it is passed through a filter is denoted by I0. In order to find the new intensity of light after traveling through the material is shown by the following equation:
I=I0cos2θ
If you pass light through two polarizing filters, you will get varied effects of polarization. If the two filters are oriented exactly perpendicular to each other, no light will pass through at all. If they are exactly parallel to each other, there will be no additional affect from the additional filter.
Polarization By Scattering and Reflecting
Unpolarized light can be polarized artificially, as well as by natural phenomenon like reflection and scattering.
learning objectives
- Calculate angle of reflection of complete polarization from indices of refraction
Polarization by Reflection
In the previous atom we discussed how polarized lenses work. In the case of polarized sunglasses, for example, when you look through them, reflected light is not entirely filtered out; reflected light can be slightly polarized by the reflection process (as shown in ). Most light sources produce unpolarized light. When light hits a reflective surface, the vertically polarized aspects of that light are refracted at that surface. The reflected light is more horizontally polarized. To better remember this, we can think of light as an arrow and the reflective surface as a target. If the arrow hits the target perpendicularly (vertically polarized), it is going to stick in the target (be refracted into the surface). If the arrow hits the target on its side (horizontally polarized) then it will bounce right off (be reflected).
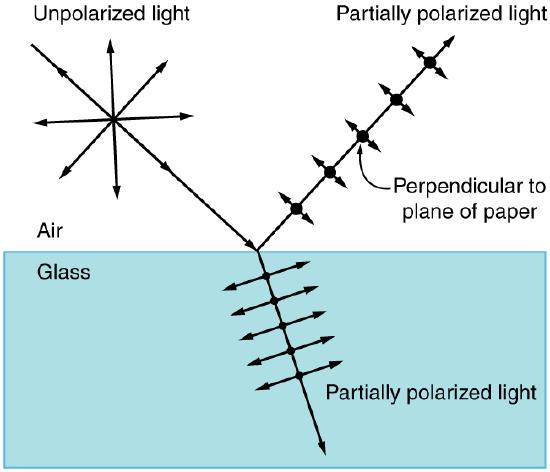
Polarization by Reflection: Unpolarized light has equal amounts of vertical and horizontal polarization. After interaction with a surface, the vertical components are preferentially absorbed or refracted, leaving the reflected light more horizontally polarized. This is akin to arrows striking on their sides bouncing off, whereas arrows striking on their tips go into the surface.
Since the light is split into two, and part of it is refracted, the amount of polarization to the reflected light depends on the index of refraction of the reflective surface. We can use the following equation to determine the angle of reflection at which light will be completely polarized:
tanθb=n2n1
where: θb = angle of reflection of complete polarization (also known as Brewster’s angle); n1 = index of refraction of medium in which reflected light will travel; and n2 = index of refraction of medium by which light is reflected.
Polarization by Scattering
Just as unpolarized light can be partially polarized by reflecting, it can also be polarized by scattering (also known as Rayleigh scattering; illustrated in ). Since light waves are electromagnetic (EM) waves (and EM waves are transverse waves) they will vibrate the electrons of air molecules perpendicular to the direction in which they are traveling. The electrons then produce radiation (acting like small antennae) that is polarized perpendicular to the direction of the ray. The light parallel to the original ray has no polarization. The light perpendicular to the original ray is completely polarized. In all other directions, the light scattered by air will be partially polarized.
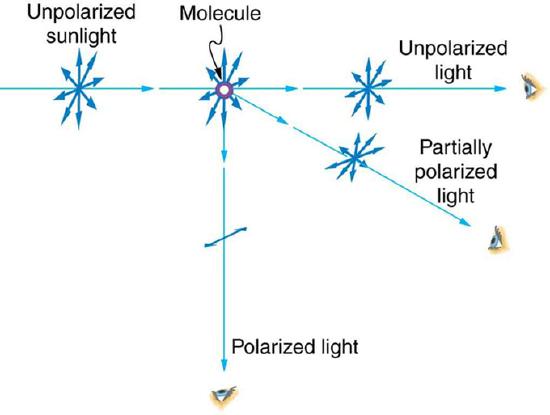
Polarization by Scattering: Also known as Rayleigh scattering. Unpolarized light scattering from air molecules shakes their electrons perpendicular to the direction of the original ray. The scattered light therefore has a polarization perpendicular to the original direction and none parallel to the original direction.
Scattering of Light by the Atmosphere
Rayleigh scattering describes the air’s gas molecules scattering light as it enters the atmosphere; it also describes why the sky is blue.
learning objectives
- Describe wave-particle relationship that leads to Rayleigh scattering and apply it to explain common phenomena
Rayleigh Scattering
Rayleigh scattering is the elastic scattering of waves by particles that are much smaller than the wavelengths of those waves. The particles that scatter the light also need to have a refractive index close to 1. This law applies to all electromagnetic radiation, but in this atom we are going to focus specifically on why the atmosphere scatters the visible spectrum of electromagnetic waves, also known as visible light. In this case, the light is scattered by the gas molecules of the atmosphere, and the refractive index of air is 1.
Rayleigh scattering is due to the polarizability of an individual molecule. This polarity describes how much the electric charges in the molecule will vibrate in an electric field. The formula to calculate the intensity of the scattering for a single particle is as follows:
I=I08π4α2λ4R2(1+cos2θ)
where I is the resulting intensity, I0 is the original intensity, α is the polarizability, λ is the wavelength, R is the distance to the particle, and θ is the scattering angle.
While you will probably not need to use this formula, it is important to understand that scattering has a strong dependence on wavelength. From the formula, we can see that a shorter wavelength will be scattered more strongly than a longer one.( The longer the wavelength, the larger the denominator, and from algebra we know that a larger denominator in a fraction means a smaller number. )
Why is the Sky Blue?
As we just learned, light scattering is inversely proportional to the fourth power of the light wavelength. So, the shorter the wavelength, the more it will get scattered. Since green and blue have relatively short wavelengths, you see a mixture of these colors in the sky, and the sky appears to be blue. When you look closer and closer to the sun, the light is not being scattered because it is approaching a 90-degree angle with the scattering particles. Since the light is being scattered less and less, you see the longer wavelengths, like red and yellow. This is why the sun appears to be a light yellow color.
Why are Sunsets Colorful?
shows a sunset. We know why the sky is blue, but why are there all those colors in a sunset? The reddening that occurs near the horizon is because the light has to pass through a significantly higher volume of air than when the sun is high in the sky. This increases the Rayleigh scattering effect and removes all blue light from the direct path of the observer. The remaining unscattered light is of longer wavelengths and so appears orange.

Sunset: A gradient of colors in the sky during sunset
Dispersion of the Visible Spectrum
Dispersion is the spreading of white light into its full spectrum of wavelengths; this phenomenon can be observed in prisms and rainbows.
learning objectives
- Describe process of dispersion
The Visible Spectrum
Within the electromagnetic spectrum, there is only a portion that is visible to the human eye. Visible light is the range of wavelengths of electromagnetic radiation that humans can see. For a typical human eye, this ranges from 390 nm to 750 nm. shows this range and the colors associated with it:

The Visible Spectrum: Visible Spectrum, represented linearly
- Violet: 380-450 nm
- Blue: 450-495 nm
- Green: 495-570 nm
- Yellow: 570-590 nm
- Orange: 590-620 nm
- Red: 620-750 nm
As you can see from, these are the colors of a rainbow and it is no coincidence.
Dispersion
Dispersion is the spreading of white light into its full spectrum of wavelengths. How does this happen? The index of refraction is different for every medium that light travels through, as we learned in previous atoms. When a light ray enters a medium with a different index of refraction, the light is dispersed, as shown in with a prism. When white light enters the prism, it spreads. Since the index of refraction varies with wavelength, the light refracts at different angles as it exits, causing the exiting light rays to appear as a rainbow, or as a sequence of decreasing wavelengths, from red to violet.
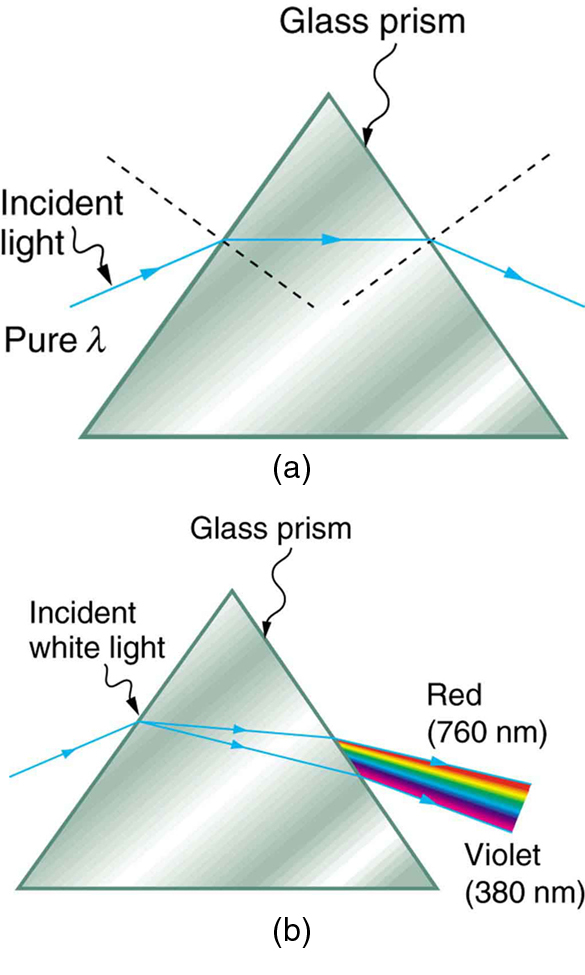
Light and a Glass Prism: (a) A pure wavelength of light falls onto a prism and is refracted at both surfaces. (b) White light is dispersed by the prism (shown exaggerated). Since the index of refraction varies with wavelength, the angles of refraction vary with wavelength. A sequence of red to violet is produced, because the index of refraction increases steadily with decreasing wavelength.
This same principle can be applied to rainbows. Refer to. Rainbows are not only caused by refraction, like prisms, but also reflection. Light enters a drop of water and is reflected from the back of the droplet. The light is refracted once as it enters the drop, and again as is exits the drop. In water, the refractive index varies with wavelength, so the light is dispersed.
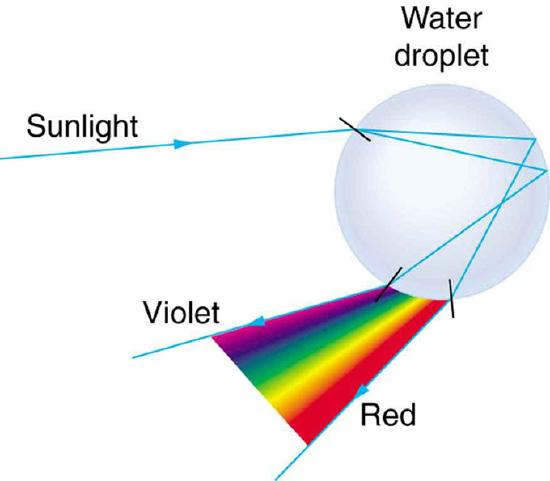
Light and a Water Droplet: Part of the light falling on this water drop enters and is reflected from the back of the drop. This light is refracted and dispersed both as it enters and as it leaves the drop.
Key Points
- When the incident light reaches the thin film, it is partially reflected and passed through to the bottom layer of the film. The difference in refractive indices of the air and film causes the light to change direction and interfere with the reflected portion of the ray when it emerges.
- This interference can be constructive, producing bright colors, or destructive, producing darker colors.
- Interference will be constructive if the optical path difference is equal to an integer multiple of the wavelength of light.
- The direction of polarization is parallel to the direction of the electric field associated with an electromagnetic wave, which includes light waves.
- By employing the polarization properties of waves, companies like Polariod how been able to produce materials that filter out unwanted waves of light, and minimize light intensity.
- Polarization materials can be oriented at different angles to produce different effects. The new intensity of light after passing through these materials can be found using the following formula: I=I0cos2θ.
- When unpolarized light hits a reflective surface, the vertically polarized aspects are refracted into the surface. The horizontally polarized aspects are reflected off the surface and the light is now perceived as partially polarized.
- When light is reflected, there is an angle at which this light is completely polarized. This is called Brewster’s angle, after the Scottish physicst who discovered the law.
- Unpolarized light can also become polarized when it is scattered in air (also known as Rayleigh scattering). This occurs due to the fact that the EM waves cause the electron in air to vibrate, producing radiation and causing polarization of the light.
- The phenomenon of light scattering is called Rayleigh scattering; it can happen to any electromagnetic waves. It only occurs when waves encounter particles that are much smaller than the wavelengths of the waves.
- The amount that light is scattered is inversely proportional to the fourth power of the light wavelength. For this reason, shorter-wavelength light like greens and blues scatter more easily than longer wavelengths like yellows and reds.
- As you look closer to the sky’s light source, the sun, the light is scattered less and less because the angle between the sun and the scattering particles approaches 90 degrees. This is why the sun has a yellowish color when we look at it from Earth while the rest of the sky appears blue.
- In outer space, where there is no atmosphere and therefore no particles to scatter the light, the sky appears black and the sun appears white.
- During a sunset, the light must pass through an increased volume of air. This increases the scattering effect, causing the light in the direct path of the observer to appear orange rather than blue.
- Dispersion is a side effect of the law of refraction. As refraction angles depend on wavelength, when light enters a medium with a different index of refraction, it can be dispersed, like a prism.
- The dispersion of white light can often cause the refracted light to be observed is in order of either increasing or decreasing wavelength, causing a rainbow effect.
- As you can see from the visible spectrum, there are some colors that the brain perceives that are not included. This is because some colors are a mixture of different wavelengths, like pink and magenta.
Key Terms
- incident ray: The ray of light that strikes the surface.
- interference: An effect caused by the superposition of two systems of waves, such as a distortion on a broadcast signal due to atmospheric or other effects.
- wavelength: The length of a single cycle of a wave, as measured by the distance between one peak or trough of a wave and the next; it is often designated in physics as λ, and corresponds to the velocity of the wave divided by its frequency.
- oscillate: To swing back and forth, especially if with a regular rhythm.
- index of refraction: For a material, the ratio of the speed of light in vacuum to that in the material.
- polarization: The production of polarized light; the direction in which the electric field of an electromagnetic wave points.
- electromagnetic radiation: radiation (quantized as photons) consisting of oscillating electric and magnetic fields oriented perpendicularly to each other, moving through space
- polarizability: The relative tendency of a system of electric charges to become polarized in the presence of an external electric field
- refraction: Changing of a light ray’s direction when it passes through variations in matter.
- reflection: the property of a propagated wave being thrown back from a surface (such as a mirror)
- dispersion: The separation of visible light by refraction or diffraction.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Thin film interference. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Thin_film_interference. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Thin Film Interference. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42519/latest/. License: CC BY: Attribution
- Thin film interference. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Thin_film_interference. License: CC BY-SA: Attribution-ShareAlike
- Paul Padley, Thin Film Interference. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m12910/latest/. License: CC BY: Attribution
- incident ray. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/incident%20ray. License: CC BY-SA: Attribution-ShareAlike
- interference. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/interference. License: CC BY-SA: Attribution-ShareAlike
- wavelength. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/wavelength. License: CC BY-SA: Attribution-ShareAlike
- Dieselrainbow. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Dieselrainbow.jpg. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: upload.wikimedia.org/Wikipedia/en/thumb/f/f1/Thin_film_interference.gif/670px-Thin_film_interference.gif. License: CC BY-SA: Attribution-ShareAlike
- Thin Film Interference. Located at: http://www.youtube.com/watch?v=Rg0WX0suVCU. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Polarization. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- Polarization (waves). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Polarization_(waves). License: CC BY-SA: Attribution-ShareAlike
- oscillate. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/oscillate. License: CC BY-SA: Attribution-ShareAlike
- Dieselrainbow. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Dieselrainbow.jpg. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: upload.wikimedia.org/Wikipedia/en/thumb/f/f1/Thin_film_interference.gif/670px-Thin_film_interference.gif. License: CC BY-SA: Attribution-ShareAlike
- Thin Film Interference. Located at: http://www.youtube.com/watch?v=Rg0WX0suVCU. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Onde cisaillement impulsion 1d 30 petit. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Onde_cisaillement_impulsion_1d_30_petit.gif. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- polarization. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/polarization. License: CC BY-SA: Attribution-ShareAlike
- index of refraction. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/index+of+refraction. License: CC BY-SA: Attribution-ShareAlike
- Dieselrainbow. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Dieselrainbow.jpg. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: upload.wikimedia.org/Wikipedia/en/thumb/f/f1/Thin_film_interference.gif/670px-Thin_film_interference.gif. License: CC BY-SA: Attribution-ShareAlike
- Thin Film Interference. Located at: http://www.youtube.com/watch?v=Rg0WX0suVCU. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Onde cisaillement impulsion 1d 30 petit. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Onde_cisaillement_impulsion_1d_30_petit.gif. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- Rayleigh light scattering. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Rayleigh_light_scattering. License: CC BY-SA: Attribution-ShareAlike
- polarizability. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/polarizability. License: CC BY-SA: Attribution-ShareAlike
- electromagnetic radiation. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/electromagnetic_radiation. License: CC BY-SA: Attribution-ShareAlike
- Dieselrainbow. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Dieselrainbow.jpg. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: upload.wikimedia.org/Wikipedia/en/thumb/f/f1/Thin_film_interference.gif/670px-Thin_film_interference.gif. License: CC BY-SA: Attribution-ShareAlike
- Thin Film Interference. Located at: http://www.youtube.com/watch?v=Rg0WX0suVCU. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Onde cisaillement impulsion 1d 30 petit. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Onde_cisaillement_impulsion_1d_30_petit.gif. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- SDIM0241b. Provided by: Wikipedia. Located at: http://en.Wikipedia.org/wiki/File:SDIM0241b.jpg. License: Public Domain: No Known Copyright
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/refraction. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Dispersion: The Rainbow and Prisms. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42466/latest/. License: CC BY: Attribution
- Visible spectrum. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Visible_spectrum. License: CC BY-SA: Attribution-ShareAlike
- dispersion. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/dispersion. License: CC BY-SA: Attribution-ShareAlike
- reflection. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/reflection. License: CC BY-SA: Attribution-ShareAlike
- Dieselrainbow. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Dieselrainbow.jpg. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: upload.wikimedia.org/Wikipedia/en/thumb/f/f1/Thin_film_interference.gif/670px-Thin_film_interference.gif. License: CC BY-SA: Attribution-ShareAlike
- Thin Film Interference. Located at: http://www.youtube.com/watch?v=Rg0WX0suVCU. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Onde cisaillement impulsion 1d 30 petit. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Onde_cisaillement_impulsion_1d_30_petit.gif. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- OpenStax College, Polarization. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42522/latest/. License: CC BY: Attribution
- SDIM0241b. Provided by: Wikipedia. Located at: http://en.Wikipedia.org/wiki/File:SDIM0241b.jpg. License: Public Domain: No Known Copyright
- OpenStax College, Dispersion: The Rainbow and Prisms. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42466/latest/. License: CC BY: Attribution
- OpenStax College, Dispersion: The Rainbow and Prisms. January 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42466/latest/. License: CC BY: Attribution
- Linear visible spectrum. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Linear_visible_spectrum.svg. License: Public Domain: No Known Copyright