5.E: Uniform Circular Motion and Gravitation (Excercise)
- Last updated
- Jul 16, 2020
- Save as PDF
- Page ID
- 26520
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
6.1: Rotation Angle and Angular Velocity
1. There is an analogy between rotational and linear physical quantities. What rotational quantities are analogous to distance and velocity?
6.2: Centripetal Acceleration
2. Can centripetal acceleration change the speed of circular motion? Explain.
6.3: Centripetal Force
3. If you wish to reduce the stress (which is related to centripetal force) on high-speed tires, would you use large- or small-diameter tires? Explain.
4. Define centripetal force. Can any type of force (for example, tension, gravitational force, friction, and so on) be a centripetal force? Can any combination of forces be a centripetal force?
5. If centripetal force is directed toward the center, why do you feel that you are ‘thrown’ away from the center as a car goes around a curve? Explain.
6. Race car drivers routinely cut corners as shown in Figure. Explain how this allows the curve to be taken at the greatest speed.
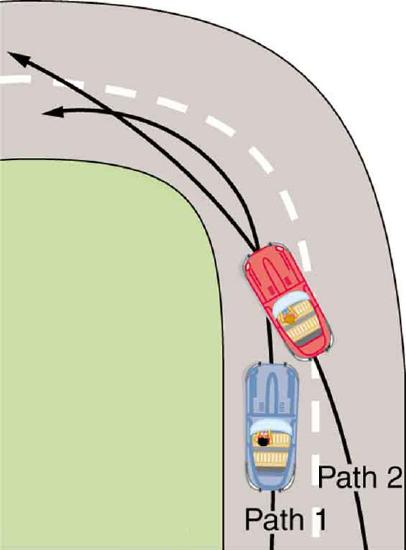
Two paths around a race track curve are shown. Race car drivers will take the inside path (called cutting the corner) whenever possible because it allows them to take the curve at the highest speed.
7. A number of amusement parks have rides that make vertical loops like the one shown in Figure. For safety, the cars are attached to the rails in such a way that they cannot fall off. If the car goes over the top at just the right speed, gravity alone will supply the centripetal force. What other force acts and what is its direction if:
(a) The car goes over the top at faster than this speed?
(b)The car goes over the top at slower than this speed?
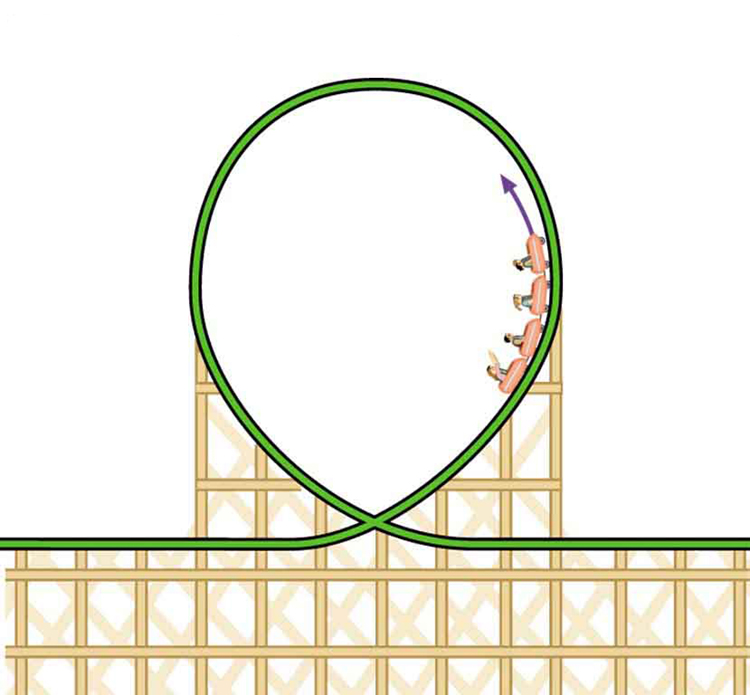
Amusement rides with a vertical loop are an example of a form of curved motion.
8. What is the direction of the force exerted by the car on the passenger as the car goes over the top of the amusement ride pictured in Figure under the following circumstances:
(a) The car goes over the top at such a speed that the gravitational force is the only force acting?
(b) The car goes over the top faster than this speed?
(c) The car goes over the top slower than this speed?
9. As a skater forms a circle, what force is responsible for making her turn? Use a free body diagram in your answer.
10. Suppose a child is riding on a merry-go-round at a distance about halfway between its center and edge. She has a lunch box resting on wax paper, so that there is very little friction between it and the merry-go-round. Which path shown in Figure will the lunch box take when she lets go? The lunch box leaves a trail in the dust on the merry-go-round. Is that trail straight, curved to the left, or curved to the right? Explain your answer.
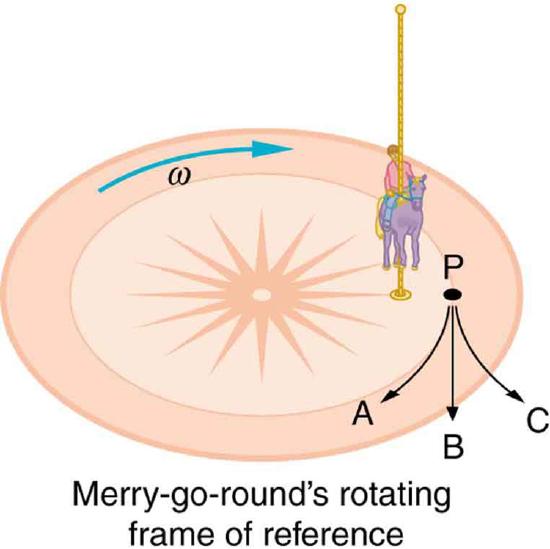
A child riding on a merry-go-round releases her lunch box at point P. This is a view from above the clockwise rotation. Assuming it slides with negligible friction, will it follow path A, B, or C, as viewed from Earth’s frame of reference? What will be the shape of the path it leaves in the dust on the merry-go-round?
11. Do you feel yourself thrown to either side when you negotiate a curve that is ideally banked for your car’s speed? What is the direction of the force exerted on you by the car seat?
12. Suppose a mass is moving in a circular path on a frictionless table as shown in figure. In the Earth’s frame of reference, there is no centrifugal force pulling the mass away from the centre of rotation, yet there is a very real force stretching the string attaching the mass to the nail. Using concepts related to centripetal force and Newton’s third law, explain what force stretches the string, identifying its physical origin.
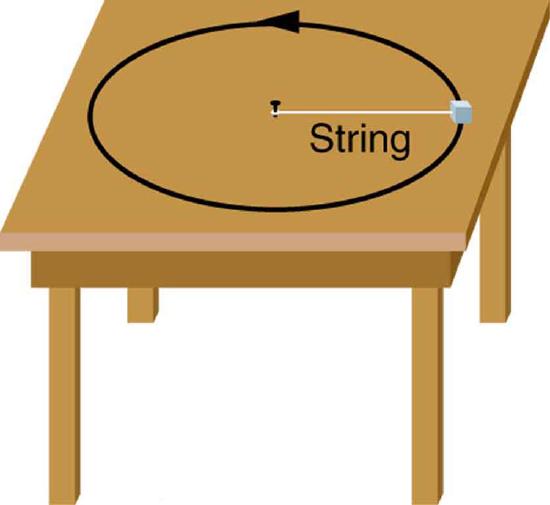
A mass attached to a nail on a frictionless table moves in a circular path. The force stretching the string is real and not fictional. What is the physical origin of the force on the string?
6.4: Fictitious Forces and Non-inertial Frames: The Coriolis Force
13. When a toilet is flushed or a sink is drained, the water (and other material) begins to rotate about the drain on the way down. Assuming no initial rotation and a flow initially directly straight toward the drain, explain what causes the rotation and which direction it has in the northern hemisphere. (Note that this is a small effect and in most toilets the rotation is caused by directional water jets.) Would the direction of rotation reverse if water were forced up the drain?
14. Is there a real force that throws water from clothes during the spin cycle of a washing machine? Explain how the water is removed.
15. In one amusement park ride, riders enter a large vertical barrel and stand against the wall on its horizontal floor. The barrel is spun up and the floor drops away. Riders feel as if they are pinned to the wall by a force something like the gravitational force. This is a fictitious force sensed and used by the riders to explain events in the rotating frame of reference of the barrel. Explain in an inertial frame of reference (Earth is nearly one) what pins the riders to the wall, and identify all of the real forces acting on them.
16. Action at a distance, such as is the case for gravity, was once thought to be illogical and therefore untrue. What is the ultimate determinant of the truth in physics, and why was this action ultimately accepted?
17. Two friends are having a conversation. Anna says a satellite in orbit is in freefall because the satellite keeps falling toward Earth. Tom says a satellite in orbit is not in freefall because the acceleration due to gravity is not 9.80 m/s2. Who do you agree with and why?
18. A non-rotating frame of reference placed at the center of the Sun is very nearly an inertial one. Why is it not exactly an inertial frame?
6.5: Newton’s Universal Law of Gravitation
19. Action at a distance, such as is the case for gravity, was once thought to be illogical and therefore untrue. What is the ultimate determinant of the truth in physics, and why was this action ultimately accepted?
20. Two friends are having a conversation. Anna says a satellite in orbit is in freefall because the satellite keeps falling toward Earth. Tom says a satellite in orbit is not in freefall because the acceleration due to gravity is not 9.80m/s2. Who do you agree with and why?
21. Draw a free body diagram for a satellite in an elliptical orbit showing why its speed increases as it approaches its parent body and decreases as it moves away.
22. Newton’s laws of motion and gravity were among the first to convincingly demonstrate the underlying simplicity and unity in nature. Many other examples have since been discovered, and we now expect to find such underlying order in complex situations. Is there proof that such order will always be found in new explorations?
6.6: Satellites and Kepler’s Laws: An Argument for Simplicity
23. In what frame(s) of reference are Kepler’s laws valid? Are Kepler’s laws purely descriptive, or do they contain causal information?
Problem Exercises
6.1: Rotation Angle and Angular Velocity
24. Semi-trailer trucks have an odometer on one hub of a trailer wheel. The hub is weighted so that it does not rotate, but it contains gears to count the number of wheel revolutions—it then calculates the distance traveled. If the wheel has a 1.15 m diameter and goes through 200,000 rotations, how many kilometers should the odometer read?
Solution
723 km
25. Microwave ovens rotate at a rate of about 6 rev/min. What is this in revolutions per second? What is the angular velocity in radians per second?
26. An automobile with 0.260 m radius tires travels 80,000 km before wearing them out. How many revolutions do the tires make, neglecting any backing up and any change in radius due to wear?
Solution
5×107 rotations
27. (a) What is the period of rotation of Earth in seconds?
(b) What is the angular velocity of Earth?
(c) Given that Earth has a radius of 6.4×106m at its equator, what is the linear velocity at Earth’s surface?
28. A baseball pitcher brings his arm forward during a pitch, rotating the forearm about the elbow. If the velocity of the ball in the pitcher’s hand is 35.0 m/s and the ball is 0.300 m from the elbow joint, what is the angular velocity of the forearm?
Solution
117 rad/s
29. In lacrosse, a ball is thrown from a net on the end of a stick by rotating the stick and forearm about the elbow. If the angular velocity of the ball about the elbow joint is 30.0 rad/s and the ball is 1.30 m from the elbow joint, what is the velocity of the ball?
30. A truck with 0.420-m-radius tires travels at 32.0 m/s. What is the angular velocity of the rotating tires in radians per second? What is this in rev/min?
Solution
76.2 rad/s
728 rpm
31. Integrated Concepts
When kicking a football, the kicker rotates his leg about the hip joint.
(a) If the velocity of the tip of the kicker’s shoe is 35.0 m/s and the hip joint is 1.05 m from the tip of the shoe, what is the shoe tip’s angular velocity?
(b) The shoe is in contact with the initially stationary 0.500 kg football for 20.0 ms. What average force is exerted on the football to give it a velocity of 20.0 m/s?
(c) Find the maximum range of the football, neglecting air resistance.
Solution
(a) 33.3 rad/s
(b) 500 N
(c) 40.8 m
32. Construct Your Own Problem
Consider an amusement park ride in which participants are rotated about a vertical axis in a cylinder with vertical walls. Once the angular velocity reaches its full value, the floor drops away and friction between the walls and the riders prevents them from sliding down. Construct a problem in which you calculate the necessary angular velocity that assures the riders will not slide down the wall. Include a free body diagram of a single rider. Among the variables to consider are the radius of the cylinder and the coefficients of friction between the riders’ clothing and the wall.
6.2: Centripetal Acceleration
33. A fairground ride spins its occupants inside a flying saucer-shaped container. If the horizontal circular path the riders follow has an 8.00 m radius, at how many revolutions per minute will the riders be subjected to a centripetal acceleration whose magnitude is 1.50 times that due to gravity?
Solution
12.9 rev/min
34. A runner taking part in the 200 m dash must run around the end of a track that has a circular arc with a radius of curvature of 30 m. If he completes the 200 m dash in 23.2 s and runs at constant speed throughout the race, what is the magnitude of his centripetal acceleration as he runs the curved portion of the track?
35. Taking the age of Earth to be about 4×109 years and assuming its orbital radius of 1.5×1011 m has not changed and is circular, calculate the approximate total distance Earth has traveled since its birth (in a frame of reference stationary with respect to the Sun).
Solution
4×1021m
36. The propeller of a World War II fighter plane is 2.30 m in diameter.
(a) What is its angular velocity in radians per second if it spins at 1200 rev/min?
(b) What is the linear speed of its tip at this angular velocity if the plane is stationary on the tarmac?
(c) What is the centripetal acceleration of the propeller tip under these conditions? Calculate it in meters per second squared and convert to multiples of g.
37. An ordinary workshop grindstone has a radius of 7.50 cm and rotates at 6500 rev/min.
(a) Calculate the magnitude of the centripetal acceleration at its edge in meters per second squared and convert it to multiples of g.
(b) What is the linear speed of a point on its edge?
Solution
a) 3.47×104m/s2,3.55×103g
b) 51.1m/s
38. Helicopter blades withstand tremendous stresses. In addition to supporting the weight of a helicopter, they are spun at rapid rates and experience large centripetal accelerations, especially at the tip.
(a) Calculate the magnitude of the centripetal acceleration at the tip of a 4.00 m long helicopter blade that rotates at 300 rev/min.
(b) Compare the linear speed of the tip with the speed of sound (taken to be 340 m/s).
39. Olympic ice skaters are able to spin at about 5 rev/s.
(a) What is their angular velocity in radians per second?
(b) What is the centripetal acceleration of the skater’s nose if it is 0.120 m from the axis of rotation?
(c) An exceptional skater named Dick Button was able to spin much faster in the 1950s than anyone since—at about 9 rev/s. What was the centripetal acceleration of the tip of his nose, assuming it is at 0.120 m radius?
(d) Comment on the magnitudes of the accelerations found. It is reputed that Button ruptured small blood vessels during his spins.
Solution
a) 31.4 rad/s
b) 118 m/s
c) 384 m/s
d)The centripetal acceleration felt by Olympic skaters is 12 times larger than the acceleration due to gravity. That’s quite a lot of acceleration in itself. The centripetal acceleration felt by Button’s nose was 39.2 times larger than the acceleration due to gravity. It is no wonder that he ruptured small blood vessels in his spins.
40. What percentage of the acceleration at Earth’s surface is the acceleration due to gravity at the position of a satellite located 300 km above Earth?
41. Verify that the linear speed of an ultracentrifuge is about 0.50 km/s, and Earth in its orbit is about 30 km/s by calculating:
(a) The linear speed of a point on an ultracentrifuge 0.100 m from its center, rotating at 50,000 rev/min.
(b) The linear speed of Earth in its orbit about the Sun (use data from the text on the radius of Earth’s orbit and approximate it as being circular).
Solution
a) 0.524 km/s
b) 29.7 km/s
42. A rotating space station is said to create “artificial gravity”—a loosely-defined term used for an acceleration that would be crudely similar to gravity. The outer wall of the rotating space station would become a floor for the astronauts, and centripetal acceleration supplied by the floor would allow astronauts to exercise and maintain muscle and bone strength more naturally than in non-rotating space environments. If the space station is 200 m in diameter, what angular velocity would produce an “artificial gravity” of 9.80m/s2 at the rim?
43. At takeoff, a commercial jet has a 60.0 m/s speed. Its tires have a diameter of 0.850 m.
(a) At how many rev/min are the tires rotating?
(b) What is the centripetal acceleration at the edge of the tire?
(c) With what force must a determined 1.00×10−15kg bacterium cling to the rim?
(d) Take the ratio of this force to the bacterium’s weight.
Solution
(a) 1.35×103rpm
(b) 8.47×103m/s2
(c) 8.47×10–12N
(d) 865
44. Integrated Concepts
Riders in an amusement park ride shaped like a Viking ship hung from a large pivot are rotated back and forth like a rigid pendulum. Sometime near the middle of the ride, the ship is momentarily motionless at the top of its circular arc. The ship then swings down under the influence of gravity.
(a) Assuming negligible friction, find the speed of the riders at the bottom of its arc, given the system's center of mass travels in an arc having a radius of 14.0 m and the riders are near the center of mass.
(b) What is the centripetal acceleration at the bottom of the arc?
(c) Draw a free body diagram of the forces acting on a rider at the bottom of the arc.
(d) Find the force exerted by the ride on a 60.0 kg rider and compare it to her weight.
(e) Discuss whether the answer seems reasonable.
Solution
(a) 16.6m/s
(b) 19.6m/s2
(c)
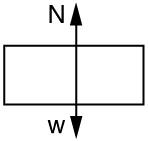
(d) 1.76×103N or 3.00w, that is, the normal force (upward) is three times her weight.
(e) This answer seems reasonable, since she feels like she’s being forced into the chair MUCH stronger than just by gravity.
45. Unreasonable Results
A mother pushes her child on a swing so that his speed is 9.00 m/s at the lowest point of his path. The swing is suspended 2.00 m above the child’s center of mass.
(a) What is the magnitude of the centripetal acceleration of the child at the low point?
(b) What is the magnitude of the force the child exerts on the seat if his mass is 18.0 kg?
(c) What is unreasonable about these results?
(d) Which premises are unreasonable or inconsistent?
Solution
a) 40.5m/s2
b) 905 N
c) The force in part (b) is very large. The acceleration in part (a) is too much, about 4 g.
d) The speed of the swing is too large. At the given velocity at the bottom of the swing, there is enough kinetic energy to send the child all the way over the top, ignoring friction.
6.3: Centripetal Force
46. (a) A 22.0 kg child is riding a playground merry-go-round that is rotating at 40.0 rev/min. What centripetal force must she exert to stay on if she is 1.25 m from its center?
(b) What centripetal force does she need to stay on an amusement park merry-go-round that rotates at 3.00 rev/min if she is 8.00 m from its center?
(c) Compare each force with her weight.
Solution
a) 483 N
b) 17.4 N
c) 2.24 times her weight, 0.0807 times her weight
47. Calculate the centripetal force on the end of a 100 m (radius) wind turbine blade that is rotating at 0.5 rev/s. Assume the mass is 4 kg.
48. What is the ideal banking angle for a gentle turn of 1.20 km radius on a highway with a 105 km/h speed limit (about 65 mi/h), assuming everyone travels at the limit?
Solution
\displaystyle 4.14º
48. What is the ideal speed to take a 100 m radius curve banked at a 20.0° angle?
49. (a) What is the radius of a bobsled turn banked at 75.0° and taken at 30.0 m/s, assuming it is ideally banked?
(b) Calculate the centripetal acceleration.
(c) Does this acceleration seem large to you?
Solution
a) 24.6 m
b) \displaystyle 36.6 m/s^2
c) \displaystyle a_c=3.73g. This does not seem too large, but it is clear that bobsledders feel a lot of force on them going through sharply banked turns.
50. Part of riding a bicycle involves leaning at the correct angle when making a turn, as seen in Figure. To be stable, the force exerted by the ground must be on a line going through the center of gravity. The force on the bicycle wheel can be resolved into two perpendicular components—friction parallel to the road (this must supply the centripetal force), and the vertical normal force (which must equal the system’s weight).
(a) Show that \displaystyle θ (as defined in the figure) is related to the speed v size 12{v} {} and radius of curvature r size 12{r} {} of the turn in the same way as for an ideally banked roadway—that is, \displaystyle θ=tan^{–1}v^2/rg
(b) Calculate \displaystyle θ for a 12.0 m/s turn of radius 30.0 m (as in a race).
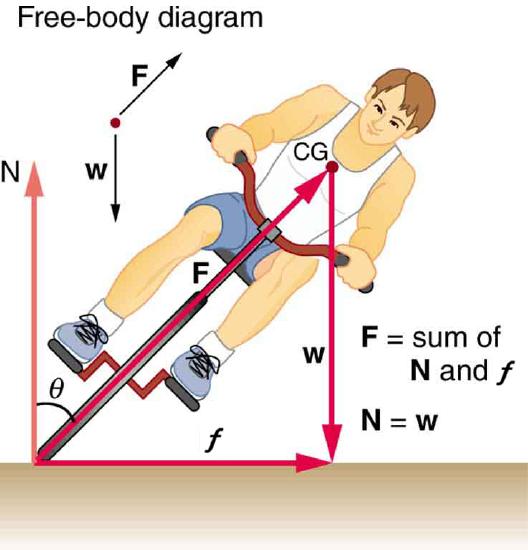
A bicyclist negotiating a turn on level ground must lean at the correct angle—the ability to do this becomes instinctive. The force of the ground on the wheel needs to be on a line through the center of gravity. The net external force on the system is the centripetal force. The vertical component of the force on the wheel cancels the weight of the system while its horizontal component must supply the centripetal force. This process produces a relationship among the angle θ, the speed v, and the radius of curvature r of the turn similar to that for the ideal banking of roadways.
51. A large centrifuge, like the one shown in Figure(a), is used to expose aspiring astronauts to accelerations similar to those experienced in rocket launches and atmospheric reentries.
(a) At what angular velocity is the centripetal acceleration \displaystyle 10g if the rider is 15.0 m from the center of rotation?
(b) The rider’s cage hangs on a pivot at the end of the arm, allowing it to swing outward during rotation as shown in Figure(b). At what angle \displaystyle θ below the horizontal will the cage hang when the centripetal acceleration is \displaystyle 10g?
(Hint: The arm supplies centripetal force and supports the weight of the cage. Draw a free body diagram of the forces to see what the angle θ size 12{θ} {} should be.)
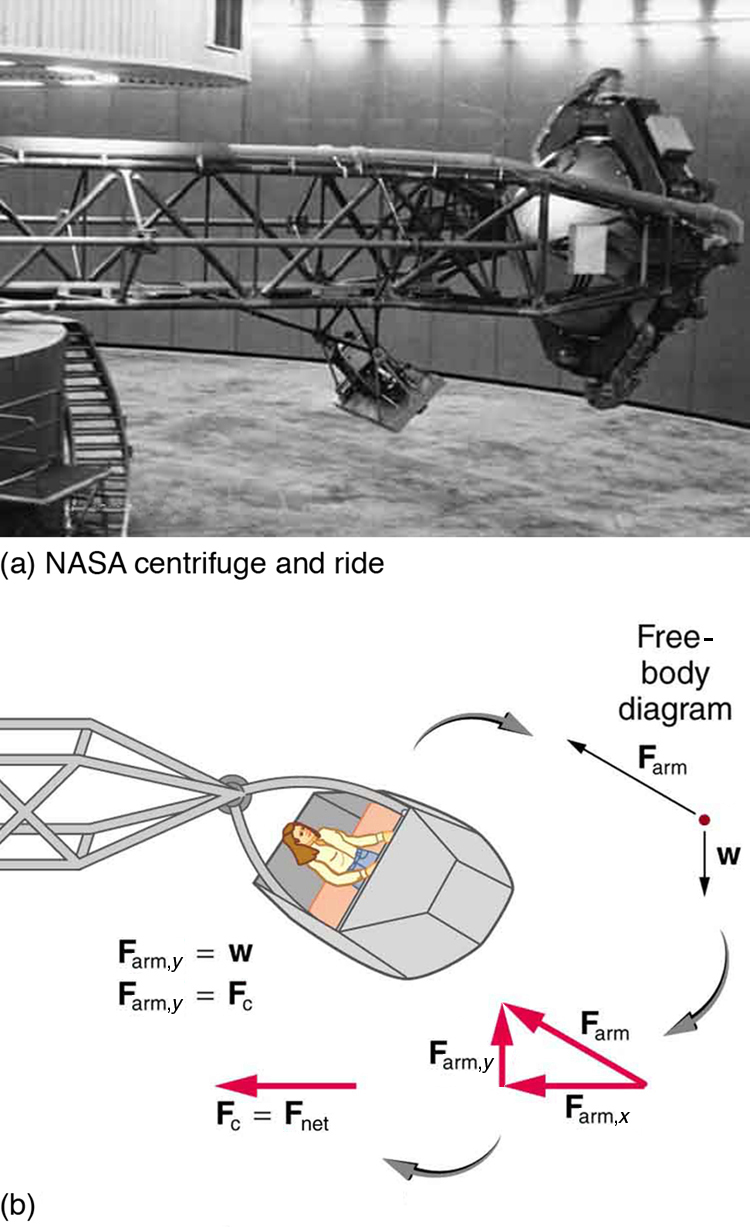
(a) NASA centrifuge used to subject trainees to accelerations similar to those experienced in rocket launches and reentries. (credit: NASA) (b) Rider in cage showing how the cage pivots outward during rotation. This allows the total force exerted on the rider by the cage to be along its axis at all times.
Solution
a) 2.56 rad/s
b) 5.71º
bIntegrated Concepts
If a car takes a banked curve at less than the ideal speed, friction is needed to keep it from sliding toward the inside of the curve (a real problem on icy mountain roads).
(a) Calculate the ideal speed to take a 100 m radius curve banked at 15.0º.
(b) What is the minimum coefficient of friction needed for a frightened driver to take the same curve at 20.0 km/h?
Solution
a) 16.2 m/s
b) 0.234
53. Modern roller coasters have vertical loops like the one shown in Figure. The radius of curvature is smaller at the top than on the sides so that the downward centripetal acceleration at the top will be greater than the acceleration due to gravity, keeping the passengers pressed firmly into their seats. What is the speed of the roller coaster at the top of the loop if the radius of curvature there is 15.0 m and the downward acceleration of the car is 1.50 g?
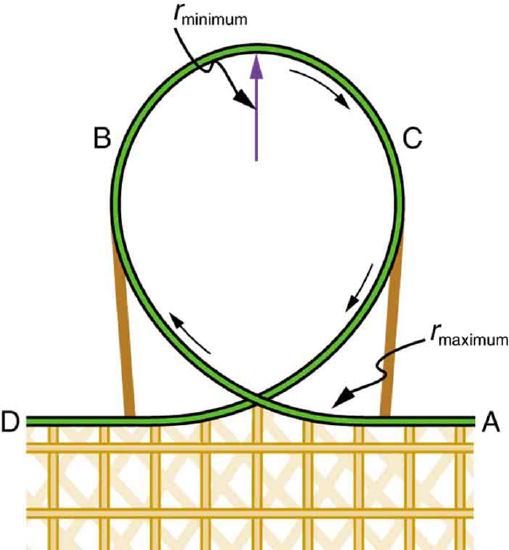
Teardrop-shaped loops are used in the latest roller coasters so that the radius of curvature gradually decreases to a minimum at the top. This means that the centripetal acceleration builds from zero to a maximum at the top and gradually decreases again. A circular loop would cause a jolting change in acceleration at entry, a disadvantage discovered long ago in railroad curve design. With a small radius of curvature at the top, the centripetal acceleration can more easily be kept greater than g so that the passengers do not lose contact with their seats nor do they need seat belts to keep them in place.
54. Unreasonable Results
(a) Calculate the minimum coefficient of friction needed for a car to negotiate an unbanked 50.0 m radius curve at 30.0 m/s.
(b) What is unreasonable about the result?
(c) Which premises are unreasonable or inconsistent?
Solution
a) 1.84
b) A coefficient of friction this much greater than 1 is unreasonable .
c) The assumed speed is too great for the tight curve.
6.5: Newton’s Universal Law of Gravitation
55. (a) Calculate Earth’s mass given the acceleration due to gravity at the North Pole is \displaystyle 9.830 m/s^2and the radius of the Earth is 6371 km from center to pole.
(b) Compare this with the accepted value of \displaystyle 5.979×10^{24}kg.
Solution
a) \displaystyle 5.979×10^{24}kg
b) This is identical to the best value to three significant figures.
56. (a) Calculate the magnitude of the acceleration due to gravity on the surface of Earth due to the Moon.
(b) Calculate the magnitude of the acceleration due to gravity at Earth due to the Sun.
(c) Take the ratio of the Moon’s acceleration to the Sun’s and comment on why the tides are predominantly due to the Moon in spite of this number.
57. (a) What is the acceleration due to gravity on the surface of the Moon?
(b) On the surface of Mars? The mass of Mars is \displaystyle 6.418×10^{23}kg and its radius is \displaystyle 3.38×10^6m
Solution
a) \displaystyle 1.62m/s^2
b) \displaystyle 3.75m/s^2
58. (a) Calculate the acceleration due to gravity on the surface of the Sun.
(b) By what factor would your weight increase if you could stand on the Sun? (Never mind that you cannot.)
59. The Moon and Earth rotate about their common center of mass, which is located about 4700 km from the center of Earth. (This is 1690 km below the surface.)
(a) Calculate the magnitude of the acceleration due to the Moon’s gravity at that point.
(b) Calculate the magnitude of the centripetal acceleration of the center of Earth as it rotates about that point once each lunar month (about 27.3 d) and compare it with the acceleration found in part (a). Comment on whether or not they are equal and why they should or should not be.
Solution
a) \displaystyle 3.42×10^{–5}m/s^2
b) \displaystyle 3.34×10^{–5}m/s^2
The values are nearly identical. One would expect the gravitational force to be the same as the centripetal force at the core of the system.
60. Solve part (b) of Example using \displaystyle a_c=v^2/r.
61. Astrology, that unlikely and vague pseudo science, makes much of the position of the planets at the moment of one’s birth. The only known force a planet exerts on Earth is gravitational.
(a) Calculate the magnitude of the gravitational force exerted on a 4.20 kg baby by a 100 kg father 0.200 m away at birth (he is assisting, so he is close to the child).
(b) Calculate the magnitude of the force on the baby due to Jupiter if it is at its closest distance to Earth, some \displaystyle 6.29×10^{11}m away. How does the force of Jupiter on the baby compare to the force of the father on the baby? Other objects in the room and the hospital building also exert similar gravitational forces. (Of course, there could be an unknown force acting, but scientists first need to be convinced that there is even an effect, much less that an unknown force causes it.)
Solution
a) \displaystyle 7.01×10^{–7}N
b) \displaystyle 1.35×10^{–6}N
62. The existence of the dwarf planet Pluto was proposed based on irregularities in Neptune’s orbit. Pluto was subsequently discovered near its predicted position. But it now appears that the discovery was fortuitous, because Pluto is small and the irregularities in Neptune’s orbit were not well known. To illustrate that Pluto has a minor effect on the orbit of Neptune compared with the closest planet to Neptune:
(a) Calculate the acceleration due to gravity at Neptune due to Pluto when they are \displaystyle 4.50×10^{12}m apart, as they are at present. The mass of Pluto is \displaystyle 1.4×10^{22}kg.
(b) Calculate the acceleration due to gravity at Neptune due to Uranus, presently about \displaystyle 2.50×10^{12}m apart, and compare it with that due to Pluto. The mass of Uranus is \displaystyle 8.62×10^{25}kg.
63. (a) The Sun orbits the Milky Way galaxy once each \displaystyle 2.60 x 10^8y, with a roughly circular orbit averaging \displaystyle 3.00 x 10^4 light years in radius. (A light year is the distance traveled by light in 1 y.) Calculate the centripetal acceleration of the Sun in its galactic orbit. Does your result support the contention that a nearly inertial frame of reference can be located at the Sun?
(b) Calculate the average speed of the Sun in its galactic orbit. Does the answer surprise you?
Solution
a) \displaystyle 1.66×10^{–10}m/s^2
b) \displaystyle 2.17×10^5m/s
64. Unreasonable Result
A mountain 10.0 km from a person exerts a gravitational force on him equal to 2.00% of his weight.
(a) Calculate the mass of the mountain.
(b) Compare the mountain’s mass with that of Earth.
(c) What is unreasonable about these results?
(d) Which premises are unreasonable or inconsistent? (Note that accurate gravitational measurements can easily detect the effect of nearby mountains and variations in local geology.)
Solution
a) \displaystyle 2.937×10^{17}kg
b) \displaystyle 4.91×10^{–8} of the Earth’s mass.
c) The mass of the mountain and its fraction of the Earth’s mass are too great.
d) The gravitational force assumed to be exerted by the mountain is too great.
6.6: Satellites and Kepler’s Laws: An Argument for Simplicity
65. A geosynchronous Earth satellite is one that has an orbital period of precisely 1 day. Such orbits are useful for communication and weather observation because the satellite remains above the same point on Earth (provided it orbits in the equatorial plane in the same direction as Earth’s rotation). Calculate the radius of such an orbit based on the data for the moon in Table.
66. Calculate the mass of the Sun based on data for Earth’s orbit and compare the value obtained with the Sun’s actual mass.
Solution
\displaystyle 1.98×10^{30}kg
67. Find the mass of Jupiter based on data for the orbit of one of its moons, and compare your result with its actual mass.
68. Find the ratio of the mass of Jupiter to that of Earth based on data in Table.
Solution
\displaystyle \frac{M_J}{M_E}=316
69. Astronomical observations of our Milky Way galaxy indicate that it has a mass of about \displaystyle 8.0×10^{11} solar masses. A star orbiting on the galaxy’s periphery is about \displaystyle 6.0×10^4 light years from its center. (a) What should the orbital period of that star be? (b) If its period is \displaystyle 6.0×10^7 instead, what is the mass of the galaxy? Such calculations are used to imply the existence of “dark matter” in the universe and have indicated, for example, the existence of very massive black holes at the centers of some galaxies.
70. Integrated Concepts
Space debris left from old satellites and their launchers is becoming a hazard to other satellites.
(a) Calculate the speed of a satellite in an orbit 900 km above Earth’s surface.
(b) Suppose a loose rivet is in an orbit of the same radius that intersects the satellite’s orbit at an angle of \displaystyle 90º relative to Earth. What is the velocity of the rivet relative to the satellite just before striking it?
(c) Given the rivet is 3.00 mm in size, how long will its collision with the satellite last?
(d) If its mass is 0.500 g, what is the average force it exerts on the satellite?
(e) How much energy in joules is generated by the collision? (The satellite’s velocity does not change appreciably, because its mass is much greater than the rivet’s.)
Solution
a) \displaystyle 7.4×10^3m/s
b) \displaystyle 1.05×10^3m/s
c) \displaystyle 2.86×10^{−7}s
d) \displaystyle 1.84×10^7N
e) \displaystyle 2.76×10^4J
71. Unreasonable Results
(a) Based on Kepler’s laws and information on the orbital characteristics of the Moon, calculate the orbital radius for an Earth satellite having a period of 1.00 h.
(b) What is unreasonable about this result?
(c) What is unreasonable or inconsistent about the premise of a 1.00 h orbit?
Solution
a) \displaystyle 5.08×10^3km
b) This radius is unreasonable because it is less than the radius of earth.
c) The premise of a one-hour orbit is inconsistent with the known radius of the earth.
72. Construct Your Own Problem
On February 14, 2000, the NEAR spacecraft was successfully inserted into orbit around Eros, becoming the first artificial satellite of an asteroid. Construct a problem in which you determine the orbital speed for a satellite near Eros. You will need to find the mass of the asteroid and consider such things as a safe distance for the orbit. Although Eros is not spherical, calculate the acceleration due to gravity on its surface at a point an average distance from its center of mass. Your instructor may also wish to have you calculate the escape velocity from this point on Eros.
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


