5.2: Static Fluids
( \newcommand{\kernel}{\mathrm{null}\,}\)
Static Fluid
A fluid is a state of matter that include gases and liquids. The distinguishing feature of fluids is that the individual molecules do not have fixed positions relative to one another, unlike in a solid. We will introduce several parameters that characterize fluids, some of which apply to solids as well. One important characteristic of fluids is pressure, which is where we begin.
What is pressure? You are familiar with this word from both everyday usage and within a scientific context. Fundamentally, pressure is an intensive property of fluids. An intensive property does not scale with the volume of the substance as energies does. Similarly temperature and density are intensive properties. While solids are characterized by temperature and density, only fluids (liquids and gases) have a characteristic pressure. For fluids, then, pressure is another state variable, telling us something about the state of the fluid system. The common use of the term “pressure” in a phrase such as “I can really feel the pressure building up inside me as finals approach; I think I’m about to explode!” somewhat captures the spirit of the meaning of pressure in a fluid. The pressure in a fluid can be changed by external means, and an increase in pressure represents an increase in energy.
Energy Perspective
Perhaps one of the most useful ways to think of pressure is as an energy density. More precisely, the pressure at a particular point in a fluid is the energy per unit volume that must be transferred from another system into the fluid system in order to create a unit volume of fluid at that point.
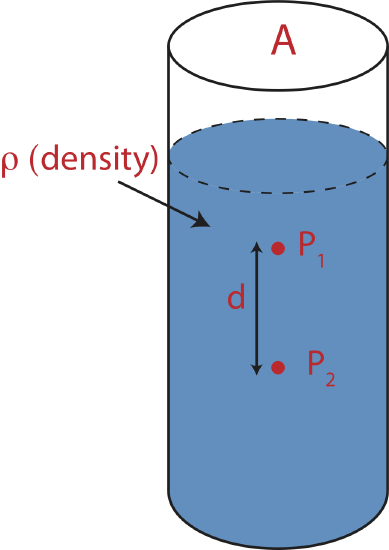
Figure 5.2.1 illustrates an a example of a static fluid in a container which is open to the atmosphere. We would like to use an energy argument to figure out how the pressure at point 1, P1, is related to pressure at point 2, P2.
In 7A we learned that energy of a system is conserved when no heat enters or leaves the system or no work is done by or on the system. The fluid in Figure 5.2.1 is in thermal equilibrium and no work is being done on the fluid. In 7A we were concerned with changes of energy as a system evolved in time from one state to another, such as ice melting on a hot day or a ball rolling down a ramp. In fluid systems at equilibrium, we are interested in looking at how energy changes in space within the fluid rather than in time.
From point 1 to point 2 in the liquid in Figure 5.2.1, there is a change of height which is an indicator of gravitational potential energy as described in Chapter 2.4. By applying the principle of conservation of energy to this closed system from position 1 to 2, we know that another energy has to increase since gravitational potential energy decreases. That energy is precisely related to pressure. In order to write down the conservation of energy equation we either have to convert gravitational potential energy into units of energy density or pressure into units of energy, since pressure has units of energy density. It is easier to work with fluid density rather than fluid mass and volume. Thus, by convention we will stick with energy densities when analyzing fluid systems. To convert an energy to an energy density we need to divide energy by volume, V. The interval of going from point 1 to point 2 is illustrated in the Energy-Interaction diagram below. This will be most likely the first and the last time we will use these diagram in 7B, but it is drawn here to help draw the connection between energy conservation in 7A to energy density conservation in 7B.
Figure 5.2.2: Energy-Interaction Diagram for a Static Fluid.
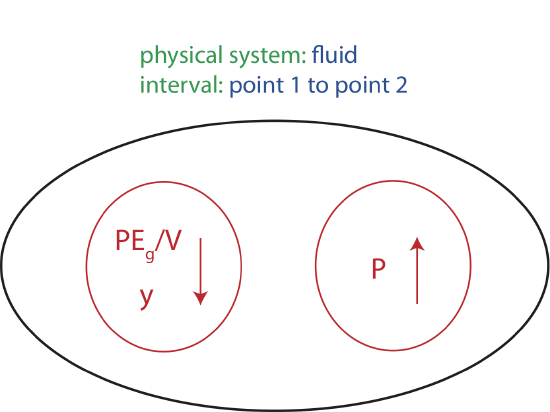
Energy conservation tells us that as we move vertically downward in a fluid at rest the gravitational potential energy density decreases so the pressure must increase by the same amount. Since the indicator of gravitational potential energies is height, it is only the change in vertical distance that matters. If we move in a horizontal direction in a fluid, the pressure remains constant.
Gravitational potential energy is given by PEg=mgy. When converted into energy density by dividing by volume V, we can further simplify the equation by using mass density, ρ=m/V, mass per unit volume.
Writing down an energy density conservation equation for the interval depicted in Figure 5.2.2:
ΔPEgV+ΔP=0
ρgΔy+ΔP=0
ρg(y2−y1)+P2−P1=0
Since y2 is at a lower height than y1, the difference between the two values will be negative or y2−y1=−d, where d is the distance between the two points as marked in Figure 5.2.1. Equation ??? becomes:
−ρgd+P2−P1=0
Solving for pressure at point 2:
P2=P1+ρgd
Example 5.2.1
In this example we want to determine the difference in pressure in air and water for the same change in height. This calculation will demonstrate why when you move from a second to the first floor (about 4 meters) in a building you do not feel a change in air pressure. However, when you dive 4 meters in water the increase in pressure is very apparent.
Calculate the change in air pressure when you descent 4 meters in air and calculate the change in water pressure when you dive down 4 meters. Use ρair∼1.2 kg/m3 and ρwater∼1100 kg/m3. You can approximate g∼10 m/s2.
- Solution
-
For air:
ΔP=−ρairgΔy=−1.2kg/m3×10m/s2×(−4.0m)=−48Pa=4.7×10−4atm
For water:
ΔP=−ρwatergΔy=−1000kg/m3×10m/s2×(−4.0m)=4×104Pa=0.4atm
Since the question asks about the change in pressure when you go down 4 meters in air or water, the change in height is negative, resulting in an increase in pressure or a positive change in pressure. The result shows that the change in water pressure is close to 1000 times greater than the change in air pressure for the same change in height.
Force Perspective
Everything we have done up to this point has treated pressure as an energy density. Pressure is also related to force, just as energy is related to force through the concept of work. Consider a piston pushing on the fluid as see in the animation below.
Figure 5.2.3: Piston Doing Work on a Fluid.

The work done by an outside agent in moving the piston a distance dx down is given by:
dW=Fdx=−PdV
Refer back to Chapter 4.2 on the relationship of work and force and pressure and volume. If a piston of area A pushes down on the fluid a distance dx, the change is volume will be dV=−Adx, resulting in Fdx=PAdx or:
F=PA
That is for a fluid system the force acting perpendicular on an area is directly proportional to the area and the fluid pressure. We can imagine that the fluid exerts this force on any area, whether it is a wall of a container or just an imaginary area separating two parts of fluid. Let us explore how we can use these ideas to determine the change in pressure with depth. Consider the forces acting on a small elements of a fluid, colored light blue (outlined by dashed lines) in the figure below.
Figure 5.2.4: Forces on an Element of Fluid.
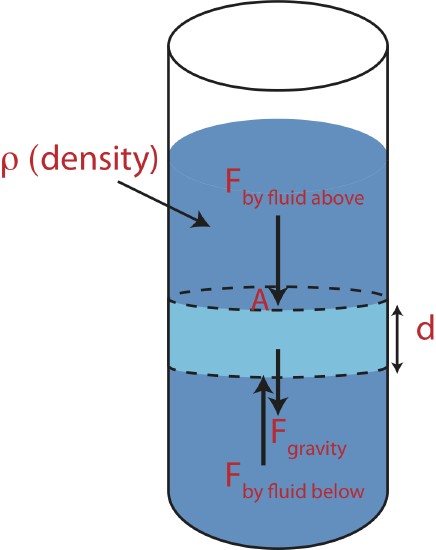
We will study forces in much more detail later in Chapter 6. The main idea to focus on here is that when a system is in equilibrium, such as a static fluid, all the forces acting on that system must be balanced. The light blue element has a force acting on it by the fluid above, Fby fluid above, a force by the fluid below it, Fby fluid below, and the force of gravity pulling it down, Fgravity as illustrated in the figure above. For the forces to be balanced, the sum of forces pushing down has to add up to the sum of the forces pushing up:
Fby fluid above+Fgravity=Fby fluid below
Plugging in F=PA and Fgravity=mg we get:
PaboveA+mg=PbelowA
Using m=ρV=ρAd we arrive at:
Pbelow=Pabove+ρgd
Comparing Equations ??? to ??? we find that the two approaches lead to an identical result. This result states that pressure in a fluid only depends on its density and the depth of the fluid and is completely independent of the amount of fluid present.
Applications
The result in Equation ??? tells us that the pressure in a fluid is the same at all points of equal height regardless of the volume of fluid above that height, such as along the dashed line in Figure 5.2.5. We can think about this by realizing that pressure does not have a direction, but represents an average forced exerted on a system per unit area. That pressure on the system, or element of a fluid, is equal in all directions. If the pressure, for example, along the dashed line in Figure 5.2.5 was greater on the right side of the container compared to the left, that would imply that the force pushing from the left would be greater than the force pushing from the right, resulting in a fluid which is not static.
This relationship between fluid pressure and depth is true as long as the fluid is:
1. static: not moving. We will see in the next section that when the fluid is moving its pressure may change even if the fluid stays at the same height.
2. continuous: the fluid density must the uniform everywhere throughout the fluid. There are no physical barriers separating parts of the fluid or two fluids of different densities in contact.
3. incompressible: there are no variations of densities within the same fluid. Thus, this relationship is most accurate when applied to liquids rather than gasses which are compressible.
Figure 5.2.5: Pascal's Principle Demonstrated.
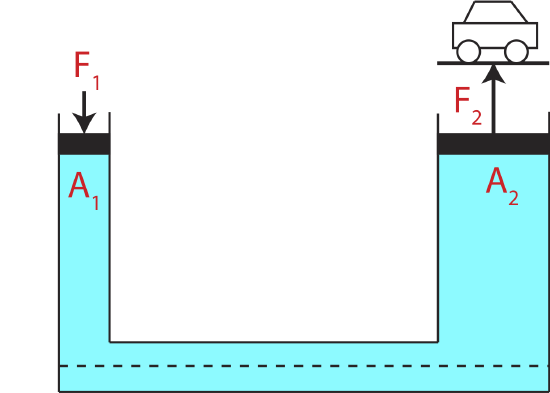
Suppose we add a constant pressure to the entire fluid, by compressing it with a piston. Then the pressure increases uniformly throughout the fluid by this same amount. Otherwise, the change in pressure due to a change in height would not be independent of the total pressure. This result is often referred to Pascal’s Principle. One common application of Pascal's Principle is hydraulic machines. Figure 5.2.5 shows an enclosed fluid with two pistons of different areas. If the pistons are at the same elevation, then the pressure in the fluid is the same, P=P1=P2. The force on each piston is simply the pressure times the area of the piston. If the small piston is pressed down with a force F1, the pressure created in the fluid is P=F1/A1. The force this pressure exerts on the larger piston is then:
F2=PA2=F1A2A1
Tremendous increases in force are readily obtained in this manner, by varying the area of the pistons appropriately. For example, this gives the piston with a larger area the ability to lift a car as shown in Figure 5.2.5. The bigger the ratio A2A1, the bigger will be the force exerted by the larger piston. Of course, the energy or power output of a hydraulic machine, as with any machine, cannot be greater than the energy or power put in. The distance the small piston has to move for a corresponding movement of the large piston is in exactly the inverse ratio of the forces, making the magnitudes of the work done by each piston the same.
A common example of a hydraulic system is the braking system of an automobile. In an “old fashioned” braking system (without power assist), pushing in on the brake pedal increased the pressure throughout the system, and uniformly applied the same force to the brake shoes on each of the four wheels. This would be tricky to do with mechanical linkages, but is “automatic” using a hydraulic system.
The fact that the pressure is the same at the same height also tells us that when a fluid meets another fluid at a boundary, the pressure of both fluids at the location of the boundary has to be the same. In Figure 5.2.1 in the open container water meets air, which means that the pressure of the water at the top is the same as air pressure, known as atmospheric pressure. It is frequently the case that the absolute pressure of a system is most easily regarded as being the sum of atmospheric pressure plus an additional pressure caused by some process. The pressure in your bicycle tires, for example, is given in lbs per square inch above atmospheric pressure, caused by the process of “pumping up your tire” which increases the pressure above atmospheric pressure. When you use a gauge to measure your tire pressure you are measuring only the increase in pressure above one atmosphere. This is called gauge pressure. A "flat tire" occurs when the air pressure inside the tire is equal to the air outside due to a leak. Thus, the tire pressure become atmospheric pressure, or zero gauge pressure. The absolute pressure is equal to the gauge pressure plus the atmospheric pressure. A good rule of thumb is when you see ΔP it refers to gauge pressure or ΔP=Pfluid−Patm, and when you see just P this refers to absolute pressure or P=ΔP+Patm.
There are many ways that pressure is measured. Generally, a device for measuring pressure is known as manometer. There are many different kinds of manometers, such as a barometer used for measuring atmospheric pressure and a sphygmomanometer used for measuring blood pressure. An example of a barometer in shown below.
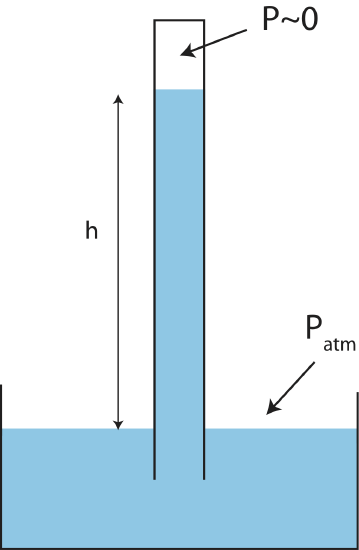
A thin long container initially filled with fluid is submerged in a large container of fluid which is open to the atmosphere as seen in Figure 5.2.6. The fluid in the thin container will flow down until pressure equilibrium is reached. We assume that the pressure at the top of the thin container is nearly zero, since air cannot enter at that end. The height of the fluid in the thin container will allow us to determine atmospheric pressure. Applying Equation ??? from the top of the thin container where the pressure is zero down a distance h at the height where the fluid in the larger container is exposed to atmosphere we get:
Patm=ρgh
Let us see what the height would have to be to measure atmospheric pressure of Patm=1atm=1.01×105Pa if water was used. Using the density of water is ρwater∼1000kg/m3 and solving Equation ??? for height, h, we get:
h=Patmρg=1.01×105Pa1000kg/m3×9.8m/s2∼10m
The height of 10m is about a three-story building! Although, we do not "feel" air pressure since our bodies are in equilibrium with atmospheric pressure, this results demonstrates the immense magnitude of atmospheric pressure if it is able to push water three stories high. It also tells us that making a water barometer is not very practical since it would require a 10 m long container and a lot of water. Using a fluid with a much larger density would allow us to use a shorter barometer. Mercury is an example of liquid with a very large density ρmercury=13600kg/m3, more than 10 times larger than the density of water. Using Equation ??? and replacing the density of water with the the density of mercury, we find that the height will be approximately 760 mm, less than 1 meter. Historically using mercury, Hg, in manometers has been so common that a unit of pressure was created based on measurements of pressure with mercury, 1atm=760mmHg. A unit of Torr is almost identical to 1 mmHg. Blood pressure is also measured in units of mmHg since mercury sphygmomanometers were commonly used before the health dangers of mercury were known.
Example 5.2.2
Intravenous infusions are usually made with the help of the gravitational force. At what height should the IV bag be placed above the entry point so that the fluid just enters the vein if the blood pressure in the vein is 18 mmHg above atmospheric pressure? Assume that the density of the fluid being administered is about the density of water 1.00 g/ml, and that the IV bag is always filled with the fluid.
- Solution
-
For the fluid to just enter the vein its pressure at entry must exceed the blood pressure in the vein (18 mm Hg above atmospheric pressure). We therefore need to find the height of fluid that corresponds to this gauge pressure, ΔP=ρgh. We need to convert the pressure and density into SI units, using 1.0mmHg=133Pa and 1.0g/ml=1000kg/m3. Solving for height:
h=ΔPρg=2394Pa1000kg/m3×10m/s2=0.24m=24cm
The IV bag must be placed at 24 cm above the entry point into the arm for the fluid to just enter the arm. Generally, IV bags are placed higher than this. You may have noticed that the bags used for blood collection are placed below the donor to allow blood to flow easily from the arm to the bag, which is the opposite direction of flow than required in the example presented here.
Example 5.2.3
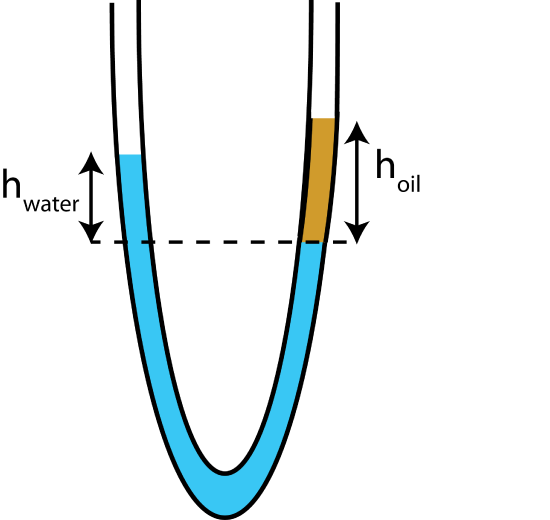
A U-shaped container with both ends open to the atmosphere, is initially fill with water. Then, some oil is slowly poured on the right side of the U-tube. Assume the oil does not mix with water and settles at levels at shown in the picture below, where hwater=18cm cm and hoil=20cm at equilibrium. Use ρwater∼1000kg/m3.
a) Find the density of oil.
b) If the ends of the tube were no longer open to the atmosphere, which side would need to have more pressure in order for the top of the water on the left side to settle at the same height as the top of the oil on the right side? Calculate this pressure difference between the two sides.
- Solution
-
a) The pressure at the dashed line in the figure is the same, since it is where water is located in one fluid system at the same height. Applying energy-density conservation equation from the open ends to the dashed line on each side:
right side of tube: ΔP+ρoilghoil=0
left side of tube: ΔP+ρwaterghwater=0
Since the pressure difference, ΔP=Patm−Pdashed line, is the same for each side, the gravitational potential energy density terms have to equal:
ρwaterghwater=ρoilghoil
resulting in:
ρoil=ρwater×hwaterhoil=1000kgm3×18cm20cm=900kgm3.
b) In this case, the heights of each fluid from a line from where the oil touches the water to the top of the fluids on each side of the tube are the same height h=20cm, since the amount of oil is the same. Let us define the pressure at the line where the two fluids touch Pdown, and the pressures at the top of the left and right sides of the U-tube Pleft and Pright, respectively. The equations become:
right side of tube: Pright−Pdown+ρoilgh=0
left side of tube: Pleft−Pdown+ρwatergh=0
Subtracting the two equations:
Pright−Pleft+(ρoil−ρwater)gh=0
Pright−Pleft=(ρwater−ρoil)gh=(1000−900)kgm3×10ms2×0.2m=200Pa


