2.4: Effects of Force on Motion

Simple Cases First

What follows is the most important step we need to take in our discussion of forces, in that it links what we have been learning in this chapter about forces to what we learned in the previous chapter about motion. Following the procedure we have established already, we will begin by considering the simplest cases first, and then expand what we learn there into more complex scenarios. To that end, we begin by considering the effect of forces on particles only, and will address the effects of force on collections of particles afterward.

Newton's Second Law

We have built some tools for analyzing situations where forces act on objects (force phrase, FBDs), and we know that there can only be accelerations when forces are present (first law). But we still are not yet able to describe the motion of a particle under the influence of one or more forces. That’s because the first law only tells us qualitatively what is happening. In physics we seek to develop quantitative models, and that’s where the second law comes in. It is really just a more detailed description of the first law, or alternatively, the first law is just a special case of the second law.

We know that force is related not to velocity (because the first law says that constant velocity exists in the absence of force), but rather the change of velocity. More specifically, the rate of change of the velocity – the acceleration. Newton defined force in the simplest possible fashion in terms of acceleration – with a linear relationship. He reasoned that pushing equal amounts on two particles of different masses resulted in different changes of motion, so he stated that the relationship between force and acceleration as a simple proportionality:

\[ \text{acceleration of particle} = \dfrac{\text{force acting on particle}}{\text{mass of particle}} \]

The idea is that for a given force, the reaction of the particle (in the form of an acceleration) is inversely-proportional to the amount of mass the particle possesses. Let’s take a moment to mention units:

\( \left[ F \right] = \dfrac{kg \cdot m}{s^2} = \; \text{"Newtons"} \; \left( N \right) \)

There is much more detail lurking in here. First of all, acceleration and force are both vectors, while mass is a scalar, so the second law is actually a vector equation:

\[ \overrightarrow a = \frac{\overrightarrow F}{m} \]

This means that the acceleration experienced by a particle is just a scaled vector of the force exerted on the particle. That is, the acceleration and the force always point in the same direction (mass is never negative). Of course, this scaling also changes the units.

ALERT

Most people first encounter Newton's second law expressed as \( \overrightarrow F = m \overrightarrow a\). While this is mathematically equivalent to what is above, it is very dangerous to write this way, as it encourages a very common misconception. We write it as we do above to emphasize the interpretation: "the effect on the motion (the acceleration) results from the cause (the force), moderated by a property of the object experiencing the effect (the mass)." The danger of using the other expression is that it reads like, "the force of the particle equals the mass of the particle multiplied by the acceleration of the particle." This turns the quantities of force and acceleration into properties of the particle, rather than cause and effect, and this leads to subtle-but-important misconceptions.

We aren’t done modifying the second law to its proper form yet! A large number of forces can be on a particle at the same time, so which force is the one that causes the acceleration? All of them. Do we figure out the accelerations of each force and then add them up? That makes no sense physically – particles do not experience lots of accelerations at once. Instead, we take all of the forces together and add them as vectors to create a single composite force that we call the net force, and that is what goes into the equation:

\[ \overrightarrow a = \dfrac{\overrightarrow F_{net}}{m} \]

Collections of Particles

Now that we have the basics of Newton's second law for particles, we would like to apply it to the many macroscopic forces we have discussed, but those forces all involve interactions with collections of particles, so we need to see if we can extend the reach of the second law. Here is the problem: If a force acts on a subset of particles in a collection (e.g. a normal force only acts on the particles at the surface of an object), then those particles will be accelerated, while other particles will not. In such situations where multiple particles in a collection are accelerating differently, how do we define the "acceleration of the full group"? There is actually a mathematical answer to this! Let's look at the simplest possible example first...

Figure 2.4.1 – Force Acts on One Particle in a Pair of Identical Particles

Here we have a force with magnitude \(F\) acting in the \(+x\)-direction one particle in a pair of particles. According to Newton's second law, we know how this particle reacts to this force:

\[a_1=\dfrac{d^2x_1}{dt^2}=\dfrac{F}{m}\]

But we want to see if we can somehow apply the second law to the combination of the two particles, which would look like this:

\[a_{pair}=\dfrac{d^2x_{pair}}{dt^2}=\dfrac{F}{m_{pair}}=\dfrac{F}{2m}\]

The problem we have here is how do we define the position of the pair, \(x_{pair}\)? Given that the two masses were equal, it seems reasonable to define the halfway point between the particles to be the "pair's position". Will this work? Mathematically, we express this as \(x_{pair} = \dfrac{x_1+x_2}{2}\), and plugging this in above, we see that in fact the answer is yes. Noting that the second derivative of \(x_2\) is zero because that mass is unaffected by the force, we get agreement:

\[\dfrac{d^2}{dt^2}x_{pair}=\dfrac{d^2}{dt^2}\left(\dfrac{x_1+x_2}{2}\right)=\dfrac{F}{2m}\;\;\;\Rightarrow\;\;\;\dfrac{d^2x_1}{dt^2}=\dfrac{F}{m}\]

Figure 2.4.2 – Force Acts on One Particle from a Pair of Particles with Different Masses

This time the extension to the pair is a little different:

\[a_1=\dfrac{d^2x_1}{dt^2}=\dfrac{F}{m_1}\;\;\;\;\; a_{pair}=\dfrac{d^2x_{pair}}{dt^2}=\dfrac{F}{m_{pair}}=\dfrac{F}{m_1+m_2}\]

Looking at what happened above, it's clear that picking the midway point between the two particles no longer works. If we think of the center point between two equal masses as the "average position" of the total mass of the pair, then when the masses are unequal, we would not expect the average position to be halfway between them. The simplest "try" is to choose an average location that is closer to the heavier particle, by an amount in proportion to their masses. The formula that accomplishes this is:

\[x_{pair}=\dfrac{m_1x_1+m_2x_2}{m_1+m_2}\]

So if the masses are equal (\(m_1=m_2=m\)), then we get the result above. If \(m_2\) is twice as massive as \(m_1\), then the "pair's location" is twice as far from \(m_1\) as it is from \(m_2\). So let's try this:

\[\dfrac{d^2}{dt^2}x_{pair}=\dfrac{d^2}{dt^2}\left(\dfrac{m_1x_1+m_2x_2}{m_1+m_2}\right)=\dfrac{m_1\dfrac{d^2x_1}{dt^2}+m_2\cancelto{0}{\dfrac{d^2x_2}{dt^2}}}{m_1+m_2}=\dfrac{F}{m_1+m_2}\]

It works! Just to recap what we have found here: If we have a pair of particles, and we define the "position of the pair" to be the precise point described by Equation 2.4.8, then the acceleration of the pair (defined as the second derivative of its position, of course) equals the force on the pair divided by the mass of the pair, even though the force only acts on one of the particles in the pair. But this definition of the location of the pair of particles works in far more general cases than this.

Exercise

Show that in the two particle example above, the definition of position of the pair given by Equation 2.4.8 gives the correct result for the case when a force \(F_1\) acts on particle 1 and a force \(F_2\) acts on particle 2 (both along the \(x\)-axis).

Solution

Both particles are now accelerated independently by different forces, and their accelerations are given by:

\[a_1=\dfrac{d^2x_1}{dt^2}=\dfrac{F_1}{m_1}\;\;\;\;\;a_2=\dfrac{d^2x_2}{dt^2}=\dfrac{F_2}{m_2}\nonumber\]

Now let's look at the acceleration of the pair:

\[a_{pair}=\dfrac{d^2}{dt^2}x_{pair}=\dfrac{m_1\dfrac{d^2x_1}{dt^2}+m_2\dfrac{d^2x_2}{dt^2}}{m_1+m_2}=\dfrac{m_1a_1+m_2a_2}{m_1+m_2}=\dfrac{F_1+F_2}{m_1+m_2}\nonumber\]

The sum \(F_1+F_2\) is the net force on the pair (you have to add together all the forces acting on any particles to get the net force), which shows that the acceleration of the pair equals the net force on the pair divided by the pair's mass.

What we have been calling the "position of a collection of particles" is commonly referred to as the center of mass of that collection. Above we have restricted it to two particles along the \(x\)-axis, but it is easy enough to generalize. If the particles have \(y\) and/or \(z\) coordinates, then the center of mass in the \(y\) and/or \(z\) directions can be defined in the same way as it was for the \(x\)-direction. And if we want to add more particles, we just include each one's position multiplied by the mass in the numerator sum, and of course make the denominator the total mass of all the particles. Putting it all together, we can write the definition of the center of mass in terms of position vectors of all the particles:

\[ \begin{array}{l} \overrightarrow r_{cm} & = x_{cm}\;\widehat i + y_{cm}\;\widehat j + z_{cm}\;\widehat k \\ & = \dfrac{\left[m_1 x_1 +m_2 x_2 + \dots \right] \widehat i + \left[m_1 y_1 + m_2 y_2 + \dots \right] \widehat j + \left[m_1 z_1 + m_2 z_2 + \dots \right] \widehat k}{M} \\ & = \dfrac{m_1 \left[x_1 \widehat i + y_1 \widehat j + z_1 \widehat k \right] + m_2 \left[x_2 \widehat i + y_2 \widehat j + z_2 \widehat k \right] + \dots }{M} \\ & = \dfrac{m_1 \overrightarrow r_1 +m_2 \overrightarrow r_2 + \dots}{M} \end{array} \]

Using this as the position of the collection of particles, that collection's acceleration works perfectly with Newton's second law, no matter how the forces on the group are distributed amongst the particles. We therefore put it all together with "\(a_{cm}\)" referring to the acceleration of the group's center of mass:

Newton's Second Law of Motion

\[\overrightarrow a_{cm}=\dfrac{\overrightarrow F_{net}}{m}\]

So now we have a robust law we can use for real objects and the composite forces we enumerated in a previous section. While this law works for any collection of particles, in almost all of our applications, the group of particles will be rigid objects. In these cases, using the center of mass is significantly easier than above, where we have to add a bunch of terms representing all of the particles. For example, if the rigid object isn't rotating, then the motion of its center of mass is identical to the motion of every particle in the collection. Introductory physics classes spend a lot of time on examples like this, which explains why Newton's second law is frequently described with no mention of center of mass at all. But even the simplest of questions cannot be answered without this knowledge. Suppose that a force is applied perpendicularly to a rigid rod at its end. It will clearly start to spin as well as move forward, which means the particles comprising the rod are all accelerated different amounts.

Figure 2.4.3 – What Part of an Extended Object Accelerates According to the Second Law?

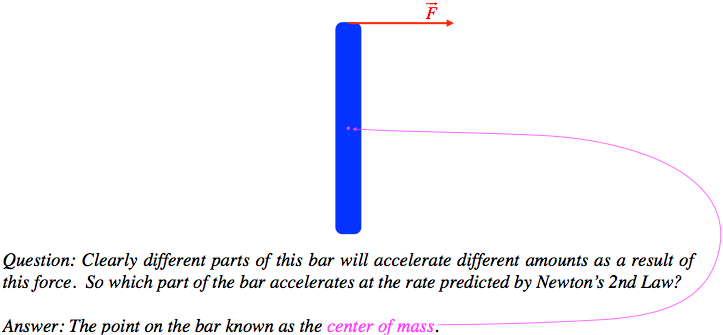
The case of a rigid object like this bar does raise an interesting question: What do we do with the forces that particles within the collection exert on each other? Such forces are necessary for the object to remain rigid. To answer this question, let's zoom-in on just two particles within the collection. One of the particles is pushed by the outside force, and as it starts to accelerate, it pulls or pushes on the other particle, to keep their structure rigid. Let's call this internal force on particle 2 by particle 1 "\(\overrightarrow F_{int}\)". According to Newton's third law, there must also be present within the collection an "evil twin" force acting on particle 1 by particle 2 exactly equal to \(-\overrightarrow F_{int}\). So when we add up all the forces on the collection, these two forces must be included (since they both act on particles within the group), but as they are equal magnitude vectors in opposite directions, they just cancel in the sum. This will be true for any pair of particles within the collection that we care to name, so we can essentially ignore the internal forces altogether.

Second Law Misconceptions

Nearly everyone reading this textbook has encountered Newton's second law before, even if it was as far back as a science class in middle school. It's unlikely that the reader has seen the discussion of center of mass before, but when it comes to the final result, many feel like they "know it already." But knowing an equation is very different from understanding what it means, so we will take some time here to try to root out some common misconceptions about this law held by even the most dedicated physics students that have seen this before. We will find that many, if not all, of these misconceptions can be avoided by keeping the following two things in mind:

• The second law mathematically expresses a cause & effect relationship, with the cause being a combination of many forces on the object, and the effect being that object's (center of mass) acceleration (not its velocity!). It is not an equality that expresses a relationship between several properties of the object.
• It is not enough to describe a force that is present in a physical situation – to put it into Newton's second law, it must be acting on the collection of particles, and it must be caused by another entity that is external to that collection. Liberal use of the force phrase and free-body diagrams is very helpful in sorting this out.

There is no better way to demonstrate what the most common misconceptions are, or show how the two reminders above helps to sort them out than to look at examples. The reader is strongly urged to commit to an answer in each case before reading the solution – this provides maximal benefit.

First a question that addresses the problem of identifying what forces get plugged into the equation for Newton's second law:

Conceptual Question

A driver steps on the brake pedal of her car, slowing the car down, and her body experiences an acceleration as a result. Which of the following forces does Newton’s second law include when determining her acceleration?

1. normal force by driver’s foot on the brake pedal
2. friction force by the car tires on the road
3. friction force by the road on the car tires
4. all of these
5. none of these

Solution

(e) One must be very precise when it comes to identifying forces, as ultimately they must be plugged into a mathematical formula. It is not enough that a force sets off a chain of events that leads to an acceleration, it must be the direct effect of that acceleration in order to be the force that is featured in the second law. In addition to being a direct force, it isn't even sufficient to isolate the correct interaction – the specific "twin" from the third law force pair must be identified. That is, the force must be on the object in order to accelerate it. The problem asks what force slows down her body. The normal force on the brake pedal affects the motion of the brake pedal. The friction force on the road affects the motion of the road. The friction force on the tires (which are part of the car's "collection of particles") affects the motion of the car. While parts of the car (namely tension by the seatbelt, friction by the car seat, and normal force by the steering wheel) do slow her down, and the friction force on the tires slows down the car, this chain of events does not mean that the friction force slows her down. If you plug the friction force on the tires and her body's mass into the second law, the acceleration you calculate for her will not be correct.

If all of that discussion still confuses you, consider what you would draw for a free-body diagram here. We are interested in the acceleration of an object (the driver), so that is the free-body that we need to draw. Next we need to add force vectors to this diagram, which, according to the force phrase, are acting on the free-body. If the description of the force does not include the phrase "on the driver", then it does not belong on the FBD, and does not figure into the calculation of the driver's acceleration according to the second law.

Next we consider what the acceleration in Newton's second law really means, and how its direction matches the direction of the net force: 

Conceptual Question

A boy throws a ball straight up, and catches it when it returns. Which pair of diagrams best represents the directions of the net forces experienced by the ball when it hits the peak of its flight (i.e. when it isn’t moving), and while the boy is catching it (i.e. not after he has caught it)?

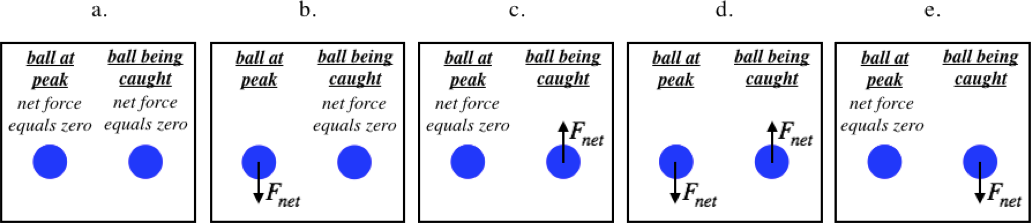
Solution

(d) Gravity is always acting on the ball, no matter where it is. When it reaches its peak, there are no other forces on it (the boy’s hand is no longer in contact with it), so the gravity force is the net force, and it points down. When the ball is in the process of being caught, gravity is still acting, but there is also a force up on it by the boy’s hand. The ball is moving downward and is slowing, so it is acceleration vector points upward, which means the force from the boy's hand exceeds the force of gravity and the net force is upward.

This question addresses the role of mass in the second law, as well as the notion of "inertia":

Conceptual Question

A stone is dropped to the ground. As it falls, the stone accelerates (without air resistance) at \(9.80\frac{m}{s^2}\) downward. As a result of this gravity force interaction, what happens to the Earth?

1. It accelerates upward toward the stone at \(9.80\frac{m}{s^2}\).
2. It accelerates upward toward the stone at a rate less than \(9.80\frac{m}{s^2}\).
3. It doesn’t accelerate - it only exerts a gravity force, it doesn’t feel it.
4. It doesn’t accelerate - it has too much inertia.
5. both (c) and (d)

Solution

(b) The magnitude of the gravity force on the stone by the Earth equals (according to Newton’s third law) the magnitude the gravity force on the Earth by the stone.  Yes, the stone exerts a gravity force on the Earth, and it is equal to the force the Earth exerts on the stone!  So why don’t we feel the Earth lurch upward when we drop something?  The magnitude of acceleration of an object with a force on it is given by the second law to be \(a=\dfrac{F}{m}\).  The Earth and the stone feel equal forces, but the Earth’s mass is much, much bigger, so it reacts to the same force with an acceleration is much, much less.  This acceleration is much too small for us to feel (the Earth's mass is about 5,972,190,000,000,000,000,000,000 kilograms).

Note that the (wrong) idea most people have of "inertia" is that it expresses a threshold. That is, they think that a certain minimum amount of force is required to "overcome" an object's inertia, and the more massive that object is, the higher that minimum force is. In the example above, this leads to the explanation that the Earth's mass is so great that there is no way that the gravity force from a stone can possibly equal the minimum force needed for acceleration. But this is not what the second law tells us! The Earth does accelerate, no matter how small the force might be.

Where does this notion of inertia come from? We see cases all the time in everyday life where this trait seems to be exhibited: We can easily get a chair to start sliding across a floor, but it takes a great deal more force to get a huge couch to start sliding. We internally reason that since the couch is more massive, this must be the property that accounts for the "inertia" that requires a threshold force to overcome. But from our earlier study of friction, we see that what is really causing this threshold effect is static friction. We must push harder than the maximum static friction force. This maximum is partly determined by the normal force between the surfaces. This normal force comes from the fact that gravity pulls the couch down to the floor. And the gravity force is greater when the object is more massive. So a more massive object exerts a greater normal force, which results in a greater maximum static friction force, which increases the threshold force needed to get it accelerating. Whew, now we see one reason why physics is so hard – one quantity (mass) can have an effect on another (minimum force to get something moving), but they are only related very indirectly under specific (but common) circumstances, and if we oversimplify the explanation ("inertia"), we get everything wrong when those circumstances are changed.

Here's a question with a bit of arithmetic:

Conceptual Question

A car with a mass of \(2000 kg\) is moving in a straight line and has an acceleration vector of magnitude \(4\frac{m}{s^2}\) pointing to the east just before it crashes into another car that is stationary.  What force does the stationary car exert on the incoming car?

1. \(8000N\) to the east
2. \(8000N\) to the west
3. \(8000N\), but the direction can only be determined if one knows whether the car was speeding up or slowing down
4. \(0N\) - the equal-and opposite forces between the cars cancel out
5. The information given is not relevant to answering the question.

Solution

(e) This is one of the most common misconceptions among people who first encounter Newton’s second law.  They think that an object “has” an acceleration, and it “has” a mass, so obviously it “has” a force equal to \(ma\) as well, and when it hits something else, that is the force that it hits with.  But acceleration is the result of a net force not a component of it. So the acceleration and mass of the incoming car tells us the net force on the car that is causing the acceleration prior to the collision. When the collision occurs, the circumstances (i.e. external forces on the car) change, which means that the car's acceleration changes – the car doesn't "remember" the acceleration it had before! Without being given this new acceleration, we can't use the car's mass to compute the net force on it.

Okay, so there was no arithmetic to be done there after all. This misconception is so prevalent that the reader is strongly encouraged to not move on from here until they have sorted it out.

Here's a question that combines a couple of ideas:

Conceptual Question

Two cars are in contact with their front bumpers, and are pushing against each other. As they do, the red car is rolling forward and the blue car is rolling backward at a constant speed. Which of the following is true:

1. The red car exerts a net force on the blue car.
2. We know that the net force on the two-car combination is zero, because the combination is not accelerating.
3. The pair of cars is not accelerating because the contact force of the red car on the blue car equals the contact force of the blue car on the red car.
4. Two of these statements are true.
5. All of these statements are true.

Solution

(b) This question again addresses the definition of acceleration (it is not the same as velocity!). If there was a net force on the blue car, it would be accelerating, but it is moving at a constant speed in a straight line, which is zero acceleration. The pair is also moving in a straight line at a constant speed, so its acceleration is zero, which tells us that this pair is experiencing no net force. However, the contact forces between the cars are always going to be equal due to the third law, so these forces (and any others that are internal to the pair) have no say whatsoever in whether the pair accelerates. Only the outside forces (friction on the tires by the road) play a role.

And finally, let's throw in a tough one that brings in the center of mass idea:

Conceptual Question

A block starts at rest on a wedge, which itself is at rest on a horizontal tabletop, as shown in the diagram.  The contact between the block and wedge is frictionless, but the contact between the wedge and tabletop is not.  When the block is released, the block begins sliding down the plane, and the static friction with the tabletop is insufficient to stop the wedge from sliding the opposite way (though it does experience kinetic friction).  We don't know whether the block or the wedge has a greater mass. What can we say about the center of mass of the block + wedge combination?

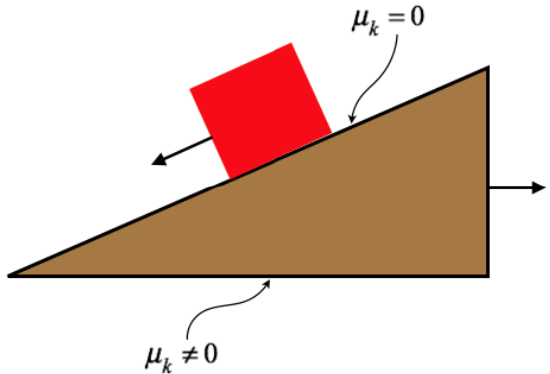
1. It accelerates straight down.
2. It accelerates down and to the right.
3. It accelerates down and to the left.
4. It accelerates down and in the same horizontal direction as the motion of the more massive object.
5. It accelerates down and in the same horizontal direction as the motion of the less massive object.

Solution

(c) It is clear that the center of mass drops, since the block descends in height and the wedge remains at the same height. The center of mass starts at rest, so it must be accelerating downward. With the two objects moving in opposite directions, it is not immediately clear what happens to the center of mass of the combination in the horizontal direction. From Newton's second law, we know that the center of mass of a combination accelerates in the same direction as the net force on it. The net force in the second law only needs to take into account the forces on the combination that are external to it – we can ignore all the internal forces. So what are these external forces? There is gravity down, a normal force up by the table (the combination of these resulting in the downward acceleration of the combination’s center of mass), and a kinetic friction force by the table opposing the wedge’s horizontal motion (i.e. pointing to the left).  Since the only horizontal external force on the combination is to the left, that is the horizontal component of the direction that the center of mass accelerates.

A Summary of Concepts Related to Newton's Laws

Much of what we have discussed in this section and the one before it will be repeated below, but putting all of these ideas in one place may help the reader consolidate the ideas into a cogent "big picture."

1. Force is not a quantity contained within an object.
2. Forces are push or pull interactions between two objects. If one looks at the two individual forces that make up the interaction, then those two forces are always equal in magnitude and opposite in direction (Newton’s third Law).
3. To avoid confusion, we learned the all-important “force phrase,” which reminds us that the individual forces that make up the interaction force pairs always act on one object and by another.
4. Forces are the cause of accelerations. It is impossible to have one of these without the other. This means that forces (if the vectors don't all cancel each other out) speed up, slow down, or change the direction of an object’s motion. And conversely, if an object’s motion slows down, speeds up, or changes direction, then it must be experiencing a (net) force. (Newton’s first Law)
5. Forces are vectors, which is to say that they have magnitude and direction.
6. The force vector that causes an object to accelerate is the net force on that object, that is, the vector sum of all of the individual forces exerted on the object. A net force is a combination of one or more real forces, but is not itself a type of force.
7. Only the forces on an object can contribute to its acceleration (i.e. added together to give the net force), never the forces by it. Forces by an object only affect the motions of the other objects that they act on.
8. The amount of net force on an object is proportional to the amount of acceleration it experiences, and the constant of proportionality is the mass, a measure of how much stuff is present in the object. (Newton’s second Law)
9. The fact that net force and acceleration are proportional means that as vectors, they must point in the same direction, since mass is never negative.
10. Mass is sometimes called “inertia,” which can be loosely thought of as resistance to acceleration. But this must not be confused with resistance to motion – the smallest net force will cause an acceleration of the largest mass. If a mass at rest doesn’t start to move when a small individual force acts on it, it is because there is another force balancing it out, causing zero net force, not because the inertia of the object cannot be overcome.
11. The part of the object (or collection of particles) that experiences the acceleration described in Newton’s second Law is the center of mass of the object, not the point on the object where the force is acting.
12. A useful tool for analyzing forces is the free-body diagram, which consists of isolating an object, followed by drawing in all the force vectors acting on it. Careful use of the force phrase helps us avoid putting incorrect forces on this diagram.