2.3: Forces as Interactions

Stepping Back

From previous sections, we now have a definition of force (push or pull between two objects), a notion of fundamental (between particles) vs. composite (between clusters of particles), and a description of all the types of composite forces we are going to encounter in this class. In this section, we will back away from the specifics of the previous section, and explore more general features of force. We will find that our faulty human intuition and imprecise language when it comes to physical concepts will give us some challenges, but hopefully this section will provide some tools for overcoming them.

Newton's Third Law

As is implied by the name “first law,” Newton was not finished – he posited two other laws of motion as well. We’ll return to the second law in a future section, but first we will discuss the third law. You have almost certainly heard it before:

Newton's Third Law

For every action there is an equal and opposite reaction.

This is an extremely unfortunate use of language, and this law has been misinterpreted for hundreds of years as a result. It is often heard quoted in movies to essentially express how natural it is to seek retribution. Something like, if someone hits you, you will hit them back afterward.

ALERT

The idea of a “reaction” as we understand it in common parlance is that it is a consequence of a previous action, but this is not the way that Newton meant it.

Okay, then, so how did Newton mean it? Forces are interactions, and just as it is impossible for a single hand to clap, it is equally impossible for a single object to be the sole participant in a force interaction. So if one object experiences a force from another, there must be a reciprocal force also felt in the other direction at exactly the same moment, with precisely the same magnitude and in precisely the opposite direction (remember, forces are vectors). So for every force you can name, there exists an evil twin that acts in the opposite direction with equal magnitude. These "twins" we will refer to as Newton’s third law force pairs. It is important to note that while all third law pairs are forces equal in magnitude and opposite in direction, not all pairs of forces equal in magnitude and opposite in direction to each other are third law pairs with each other. That is, "equal-and-opposite" is a necessary (restrictive), but not sufficient (defining) condition. It is also worth noting that this law doesn't depend upon the force being fundamental between particles, or composite between objects – it is just a general feature of force itself.

What follows is a very useful tool in our study of force, and in particular for identification of third law pairs:

The "Force Phrase"

"...\(\left<type\;of\;force\right>\) on \(\left<object\;experiencing\;force\right>\) by \(\left<object\;exerting\;force\right>\)..."

By "type of force", we mean one of the macroscopic forces listed in the previous section (gravity, contact, tension, etc.), and since two objects are always involved, both must be listed here. In addition, the specific force between the two objects must be indicated, meaning that the phrase specifies which object is doing the pushing or pulling, and which object is being pushed or pulled.  Of course they are both pushed or pulled, but that just means there are two forces involved (one acting on each object), and this force phrase singles out one of them.

This phrase can be used to great effect to identify third law pairs. If one can correctly describe a force using the force phrase, then its third-law pair is the force whose phrase simply reverses the "on" and "by" objects. Naturally the type of force must be the same for both, as they are two halves of the same single interaction.

Conceptual Question

A child sits on a swing, swinging back-and forth.  At the bottom of the swing, which of the following forces is the Newton’s 3rd law pair to the contact force the child exerts on the seat of the swing?

1. the tension force on the seat by the chain of the swing
2. the gravitational force on the child by the Earth
3. the gravitational force on the Earth by the child
4. the centripetal force on the child by the seat
5. none of these

Solution

(e) The contact force on the seat by the child is a result of the interaction of the seat and the child.  The third law pair is therefore the contact force on the child by the seat.  Forces (a)-(c) aren't the same interaction as the one given, and (d) is not even a type of force!

Conceptual Question

A block weighing 12lb travels in a circular path in a vertical plane. As the block does this, it slides along a frictionless circular track, and it is also attached to a string, the other end of which is attached to a fixed point at the center of the circle. When the block is at the bottom of its circular path, the contact force exerted on it by the track equals the tension force exerted on it by the string, and both are equal to 12lb. Which of the following forces is the Newton’s 3rd Law pair corresponding to the gravity force on the block?

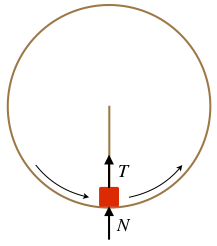
1. the normal force on the block
2. the tension force on the block
3. Either (a) or (b) can be considered a third law pair for the gravity force.
4. the sum of (a) and (b)
5. None of the above is a third law pair to the gravity force on the block.

Solution

(e) Don't let all the special information provided and coincidental numbers fool you! Just reverse the "on" and the "by" in the force phrase. The gravity force interaction is between the block and the earth, so the third law pair of the gravity force on the block by the earth is the gravity force on the earth by the block.

Free-Body Diagrams

Possibly our most powerful tool for analyzing forces and their effects on the motions of objects is the free-body diagram (or FBD for short). This is a diagram that consists of a single system (the "free-body," which can be a single object or a collection of objects with the same collective fate), with arrows representing force vectors drawn on it. There are a few rules to drawing an accurate FBD:

• It must include only an isolated "system." This system can consist of one object or many, but the analysis that follows applies to the system as a whole, and nothing outside this system – whatever its role in the physics – is included in the diagram.
• The force vectors must be “real” forces. If you can’t name the force with one of the forces mentioned earlier, then you are probably trying to fix something that isn’t broken by inventing a force. Also, no forces calculated from aggregates of other forces should be included – just separate, physically-describable forces.
• Only forces on the system can be included – never forces by the system. If every vector is labeled using the force phrase, there is no way to go wrong here.
• For now, where the force vectors are located on the system is not important, so the entire system can be reduced to a single dot for simplicity (we will discuss why we are allowed to do this for systems of particles in the next section). But later this quarter the location where the force acts will become important, so it might be a good idea to try to place the force vectors properly right away. Since the type of force and its basic nature are related to where it acts on an system, this will also help confirm that you are dealing with the right forces, and are not trying to invent a force that doesn't exist.

Okay, let's consider the following puzzling question... Suppose two people engage in a tug-o-war. According to Newton's third law, the tension force on person #1 by person #2 equals the tension force on person #2 by person #1. This is inescapable.  But then how does anyone ever win, if both always pull with the same force? Let’s draw a FBD to see if we can see why.

The first step is to isolate a single object (the "free body") – we will therefore choose one of the two competitors. Then we need to think about the physical situation, and name all the forces on (not by!) that object, and add vector arrows to the diagram to represent those forces. Only then can we decide how the motion of the free body might be affected by these forces.

Figure 2.3.1 – Analyzing a Tug-o-War Using a FBD

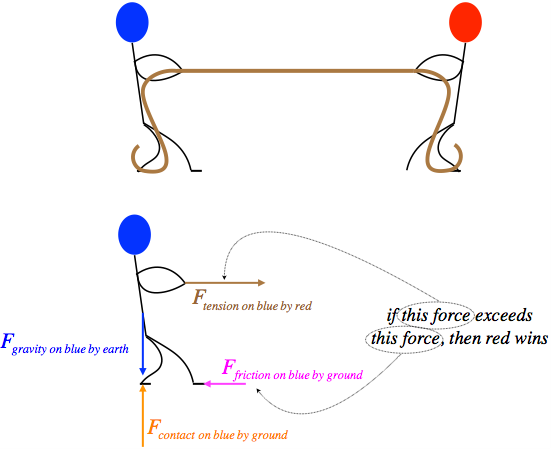
The reason the question is confusing is that we think that the two forces that are equal-and-opposite must always cancel out, but how exactly do forces “cancel?” They have to act on the same system to be added together and cancel. By drawing a careful force diagram in which we only include the forces on the system in question (in this case, the blue-headed stick figure), we see that in fact the third law pairs that are equal and opposite are split between two FBDs, and therefore cannot cancel each other. The real determining factor of whether an individual wins the tug-o-war is whether that individual receives a friction force from the ground that is greater than or less than the tension force, unbalancing the total horizontal force on them.

Does this mean the person is at the whim of the ground, that either decides to provide a big or small friction force? Of course not! The friction force on our feet by the ground is equal-and-opposite to the friction force our feet exert on the ground, and we do this by leaning back and sliding (or push our foot forward as if to slide it) across the ground. We can see that this is the case, because even the strongest human in the world cannot win a tug-o-war against a small child if the strong person is on ice or on some rolling device that doesn’t allow them to push horizontally (and thereby be pushed back the opposite way).

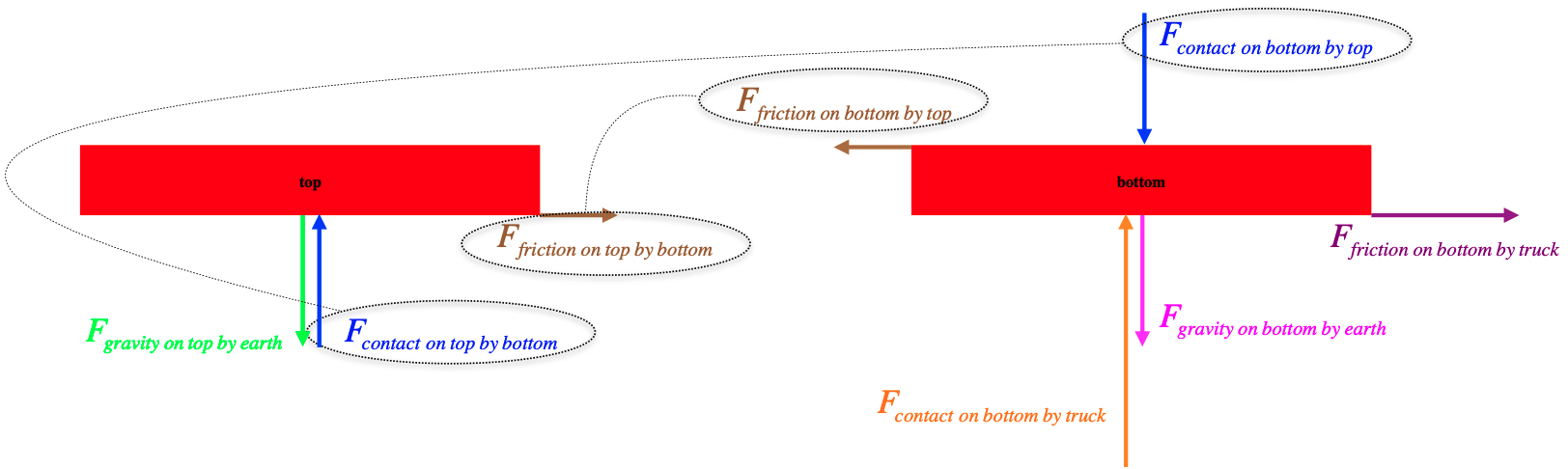
Exercise

A pickup truck with the tailgate down carries two identical sheets of plywood stacked in its bed as it accelerates horizontally.  The plywood sheets do not slide within the bed or across each other.

a. Draw a free-body diagram for both sheets of plywood, labeling the vector arrows using the force phase.

b. Indicate which forces in your diagrams are third-law force pairs of each other.

Solution