Sample Problems
- Page ID
- 63057
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)All of the problems below have had their basic features discussed in an "Analyze This" box in this chapter. This means that the solutions provided here are incomplete, as they will refer back to the analysis performed for information (i.e. the full solution is essentially split between the analysis earlier and details here). If you have not yet spent time working on (not simply reading!) the analysis of these situations, these sample problems will be of little benefit to your studies.
Problem 2.1
Two spherical objects of identical radii but different masses are dropped from different heights through the air. They both reach terminal velocity at the same moment in time, and at that moment, they are side-by-side. From this point on, the time that the heavier sphere takes to reach the ground is half the time that the lighter sphere takes.
- Find the ratio of the masses of the two spheres.
- Treating the two spheres as a single system, the constant velocities of the individual spheres assures that the system's center of mass is also moving at a constant speed. In other words, the system is also at terminal velocity. The system as a whole does not have the same cross-sectional area or the same shape as the individual spheres, so it has a different drag coefficient \(C_d\) than that of the individual spheres \(c_d\). Find \(C_d\) in terms of \(c_d\).
- Solution
-
a. Both spheres are moving at constant speeds, and they are both covering the same distance, so the times they take to reach their destination are inversely-proportional to these speeds. The heavier mass takes half the time to get to the ground, so it must be moving twice as fast. Using the result from the analysis, we find the ratio of the masses to be:
\[\dfrac{2}{1}=\dfrac{V_{terminal}}{v_{terminal}}=\sqrt{\dfrac{M}{m}}\;\;\;\Rightarrow\;\;\;M=4m\nonumber\]
b. The density of the air (\(\rho\)), cross-sectional area (\(A\)), and drag coefficient (\(c_d\)) are all the same for both cases, so given what we learned about the velocities, the drag forces on the two spheres are (capital letter symbols refer to the heavier sphere, lower-case symbols to the lighter sphere):
\[f_d=\frac{1}{2}c_d\rho A v^2\;,\;\;\;\;F_d=\frac{1}{2}c_d\rho A V^2=\frac{1}{2}c_d\rho A \left(2v\right)^2=4f_d\nonumber\]
For the system as a whole, the air density is unchanged, and the cross-sectional area is the sum of the areas of the two spheres (\(A_{sys}=2A\)). The terminal velocity of the system is the velocity of its center of mass (\(v_{cm}\)), so in terms of the new drag coefficient, the drag force on the system is:
\[F_d\left(\text{system}\right)=\frac{1}{2}C_d\rho A_{sys}v_{cm}^2\nonumber\]
Now we just need to include two more things. First, the drag force on the system is just the sum of the drag forces on the spheres:
\[F_d\left(\text{system}\right)=F_d+f_d=5f_d\nonumber\]
And second, we need the speed of the center of mass. We have the ratio of the masses from part (a), so:
\[v_{cm}=\dfrac{d}{dt}y_{cm}=\dfrac{d}{dt}\left(\dfrac{m_1y_1+m_2y_2}{m_1+m_2}\right)=\dfrac{MV+mv}{M+m}=\dfrac{\left(4m\right)\left(2v\right)+mv}{4m+m}\;\;\;\Rightarrow\;\;\;v=\frac{5}{9}v_{cm}\nonumber\]
Now we put it all together:
\[F_d\left(\text{system}\right)=5f_d=5\left[\frac{1}{2}c_d\rho A v^2\right]=5\left[\frac{1}{2}c_d\rho \left(\frac{1}{2}A_{sys}\right) \left(\frac{5}{9}v_{cm}\right)^2\right]\nonumber\]
Comparing this to the equation above allows us to extract the drag coefficient:
\[C_d = \frac{1}{2}\left(5\right)\left(\frac{5}{9}\right)^2c_d\approx 0.77c_d\nonumber\]
Problem 2.2
A sign hangs from a wire that is attached to a ring that is also attached to two wires (one of which is horizontally-oriented), as shown in the diagram. The wires and ring have negligible mass. The tension in one of the wires is three times as great as the tension in the other wire. Find the angle \(\theta\).
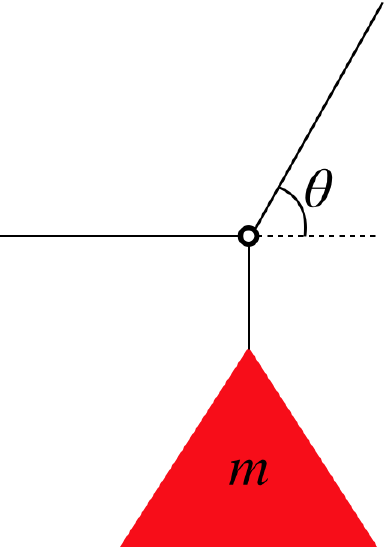
- Solution
-
In the analysis we found, among other things:
\[T_1=T_2\cos\theta\nonumber\]
The cosine is always less than or equal to 1, so the force with the greater magnitude must be \(T_2\). Plugging-in \(T_2=3T_1\) and solving for \(\theta\) gives:
\[\cos\theta=\dfrac{1}{3}\;\;\;\Rightarrow\;\;\;\theta=\cos^{-1}\left(\frac{1}{3}\right)=70.5^o\nonumber\]
Problem 2.3
A block is attached to a spring that stretches down from the ceiling of a stationary elevator that is capable of accelerating up or down. The block is then lifted slightly, and a bathroom scale is placed beneath it, so that the block rests on it. The spring is still stretched at this point, but not as fully as when the block was hanging from it. The spring constant is \(k=24.0\frac{N}{m}\), the mass of the block is \(m=6.00kg\), and in the stationary elevator the scale reads \(8.20N\).
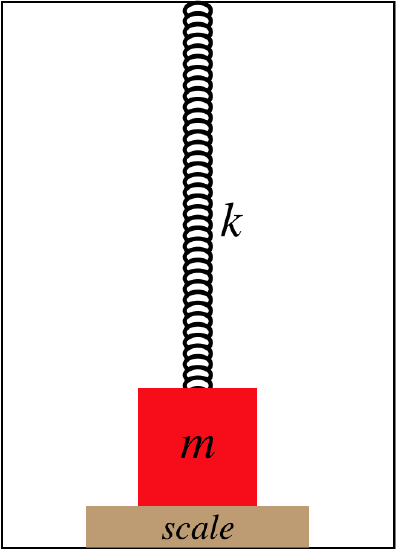
- Find the direction and minimum magnitude of the acceleration of the elevator necessary to bring the scale reading to zero.
- If the acceleration is double the value given in part (a), find how far above the scale the block rises.
- Solution
-
a. In the analysis for this situation, we found the relationship between the forces and the acceleration:
\[F_{\text{net}}=+k\Delta x+N-mg=ma\nonumber\]
The reading of the scale is the normal force, and when the elevator is not accelerating we'll call it \(N_o\), We therefore have:
\[a=0\;\;\;\Rightarrow\;\;\;N_o=mg-k\Delta x\nonumber\]
The scale reads zero at the point when the normal force goes to zero, so setting \(N\) equal to zero in the original equation above, and noting that the spring stretch and weight of the block remain the same for the cases of when the normal force just goes to zero and \(a=0\) , we get:
\[ma=+k\Delta x+0-mg=-N_o\;\;\;\Rightarrow\;\;\;a=-\dfrac{N_o}{m}=-\dfrac{8.20N}{6.00kg}=-1.37\frac{m}{s^2}\nonumber\]
The minus sign indicates that the elevator must accelerate downward, as we would expect.
b. When the block leaves contact with the scale, the normal force remains zero, and at twice the acceleration we have a new spring stretch we'll call \(\Delta x'\) Subtracting this stretch from the original stretch gives the height that the block rises, so:
\[+k\Delta x'+0-mg=m\left(2a\right)=2\left(k\Delta x-mg\right)\;\;\;\Rightarrow\;\;\;k\Delta x-k\Delta x'=mg-k\Delta x=N_o\;\;\;\Rightarrow\;\;\;\Delta x-\Delta x'=\dfrac{N_o}{k}=\dfrac{8.20N}{24.0\frac{N}{m}}=0.342m\nonumber\]
Problem 2.4
A block is sped-up at a steady rate along a rough, horizontal surface by a stretched spring that pulls on it. The coefficient of kinetic friction between the block and the horizontal surface is \(\mu_k=0.300\). as the block is being pulled in this manner, it suddenly comes upon a smooth (frictionless) region of the horizontal surface, and its acceleration instantly increases to an amount that is 250% of the original acceleration. Find the before and after accelerations.
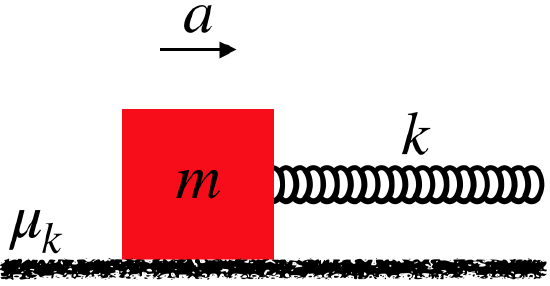
- Solution
-
In the analysis we found this:
\[-\mu_kmg+k\Delta x=ma\nonumber\]
Initially we have \(\mu_k=0.300\), and when the surface becomes smooth, this changes to \(\mu_k=0.0\) while \(a\) changes to \(a_{after}=2.50a\). The spring stretch doesn't have time to change when the block suddenly reaches the smooth area, so the value of \(k\Delta x\) remains unchanged. This gives us two equations that we can solve simultaneously for the acceleration \(a\):
\[0+k\Delta x=m\left(2.50a\right)\;\;\;\Rightarrow\;\;\; -\left(0.300\right)mg+2.50ma=ma\;\;\;\Rightarrow\;\;\;a=\frac{0.300}{1.50}g=1.96\frac{m}{s^2}\;,\;\;\;\;a_{after}=4.90\frac{m}{s^2}\nonumber\]
Problem 2.5
A tetherball swings around a pole, making a full circle at regular time intervals. The rope has negligible mass. A pebble is dropped from rest from the point where the rope is in contact with the pole. In the time it takes the pebble to cross the horizontal plane of the tetherball's circular motion, find the number of radians the tether ball has traversed of its circle.
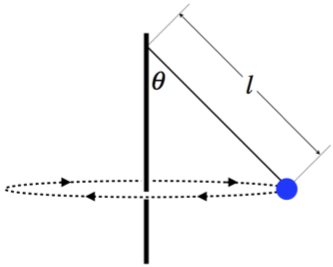
- Solution
-
The distance that the pebble travels is found from the right triangle formed by the rope and the pole (from the point where the rope is attached to the ball's rotational plane), and as it is in free-fall, this can be related to the time of the journey, starting from rest:
\[\Delta y = l\cos\theta=\frac{1}{2}gt_{drop}^2\nonumber\]
In the analysis, we found the following relationship (where "\(t\)" is the time of one full revolution of the ball):
\[\cos\theta = \dfrac{gt^2}{4\pi^2l}\;\;\;\Rightarrow\;\;\;l\cos\theta = \dfrac{1}{2\pi^2}\left(\frac{1}{2}gt^2\right)\nonumber\]
Setting these equal, we can determine what fraction of the time of a tetherball revolution is the time the pebble takes to drop:
\[\dfrac{t_{drop}}{t}=\dfrac{1}{\sqrt{2}\;\pi}\nonumber\]
In a full revolution, the tetherball sweeps out a full \(2\pi\;radians\), so in the fraction of time, it travels:
\[\Delta\Omega = \left(\dfrac{t_{drop}}{t}\right)2\pi=\sqrt 2 \;rad\nonumber\]
Problem 2.6
A large block is pushed along a horizontal, frictionless surface by an external fixed force. In contact with the rear vertical face of the large block is a smaller block, and as the two blocks are accelerated horizontally, the smaller block slides down the rough (not frictionless) face of the larger block at a constant speed. The coefficient of kinetic friction between the blocks is \(\mu_k=0.40\). The large block begins at rest, and after \(0.25s\), the small block hits the horizontal surface. At this moment, the large block has been displaced horizontally the same distance that the small block has fallen. Find the speed of the smaller block when it hits the horizontal surface.
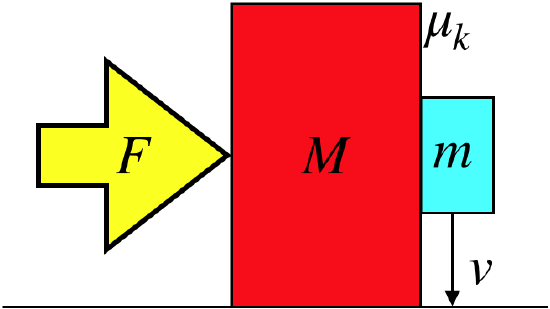
- Solution
-
The analysis gave us the force that must be applied to allow the kinetic friction force to equal; the weight of the small block (so that it doesn't accelerate vertically), and this gives us the horizontal acceleration of both blocks:
\[F=\frac{1}{\mu_k}\left(M+m\right)g\;\;\;\Rightarrow\;\;\;a=\dfrac{F}{M+m}=\dfrac{g}{\mu_k}\nonumber\]
The big block starts at rest, so after a time \(t\) is moves a distance equal to:
\[\Delta x = \frac{1}{2}at^2=\frac{g}{2\mu_k}t^2\nonumber\]
The distance the smaller block falls at a constant speed in the same time is \(v_yt\), so ssince we are given that these distances are equal, we get:
\[\frac{g}{2\mu_k}t^2=v_yt\;\;\;\Rightarrow\;\;\;v_y=\frac{g}{2\mu_k}t=\frac{9.8\frac{m}{s^2}}{2\cdot 0.40}\left(0.25s\right)=3.1\frac{m}{s}\nonumber\]
The horizontal component of the smaller block's velocity is found from its horizontal acceleration:
\[v_x=at=\frac{g}{\mu_k}t=2v_y=6.1\frac{m}{s}\nonumber\]
And the block's total speed is therefore:
\[v=\sqrt{v_x^2+v_y^2}=6.8\frac{m}{s}\nonumber\]
Problem 2.7
A system of two balls of different masses attached by a string are thrown horizontally through the air, and rotates at a steady rate about its center of mass as it goes. Air resistance is negligible for the system, and at the moment the balls are thrown, the larger ball is directly above the smaller ball, as in the diagram. The length of the string is \(15cm\), and the two-ball system makes 2 full revolutions every second. Find the amount that the height of the heavier ball has changed 1.25 seconds after the balls are released.
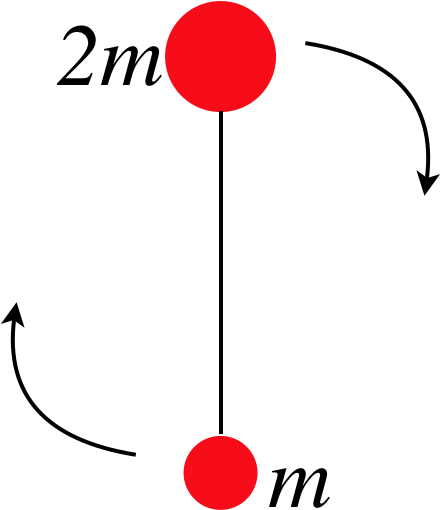
- Solution
-
This system as a whole (i.e. its center of mass) behaves like any other projectile as discussed in the analysis, and since it is launched horizontally, we can easily compute how far the center of mass falls:
\[\Delta y_{cm} = \frac{1}{2}gt^2=766cm\nonumber\]
With the system rotating at a rate of 2 revolutions per second, after 1.25 seconds it has made 2.5 revolutions, which means that the heavier ball is now directly below the center of mass. With the two masses in a 2-to-1 ratio, the center of mass half as far from the heavier ball than it is from the lighter ball. This means that it started one third of the length of the string above the center of mass, and 1.25 seconds later it was one third of the length of the string below the center of mass. So the amount it has fallen is the distance the center of mass has fallen plus an additional amount of two-thirds of the string length:
\[\Delta y_{2m} = \frac{2}{3}l+\Delta y_{cm} = \frac{2}{3}\left(15cm\right)+766cm=776cm\nonumber\]
Problem 2.8
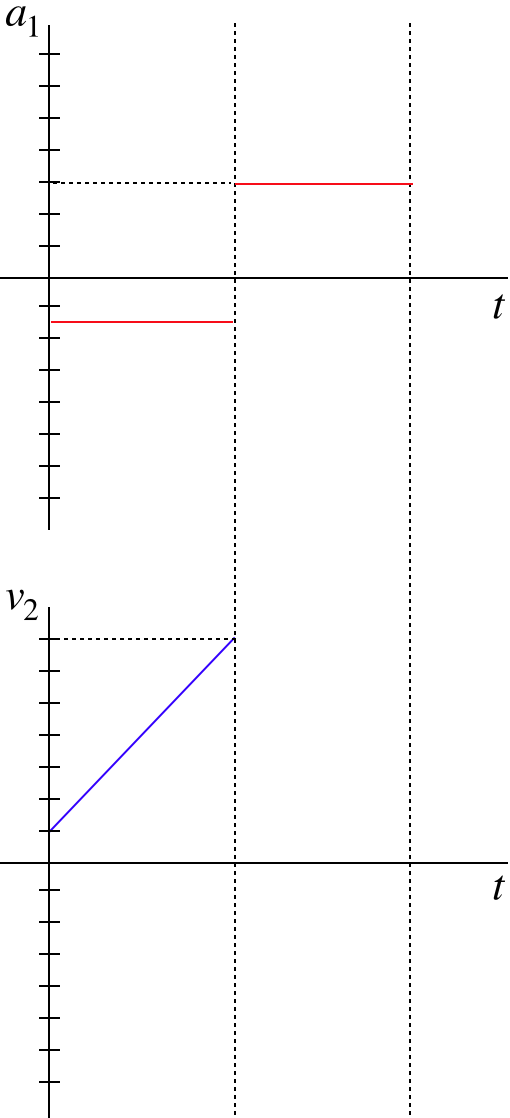
Two particles, #1 and #2 interact only with each other. The acceleration of particle #1 is plotted on the graph below for a period of time. The velocity of particle #2 was plotted simultaneously, but the data for the second half of the time interval was lost, and its graph is also shown below. Particle #1 comes to rest end of its journey.
- Fill in the missing segment of the graph.
- Plot the graph of the center of mass of this two-particle system.
- Solution
-
a. This was done in its entirety in the analysis! [It's often the case that the analysis can get us right up to the doorstep of the answer to any question, but occasionally the analysis can provide a complete answer.]
b. The particles are interacting only with each other, which means that there is no external force on this system. This means that its center of mass must maintain a constant velocity (Newton's first law). We are given that particle #1 comes to rest at the end of the journey, so we know the velocities of both particles at that moment in time, which means we can compute the unchanging velocity of the center of mass.
In the analysis, we used the second and third laws to determine the ratio of the masses of the particles, namely: \(m_1=4m_2\). This gives us the center of mass velocity:
\[v_{cm}=\dfrac{m_1v_1+m_2v_2}{m_1+m_2}=\dfrac{4\cancelto{0}{v_1}+1v_2}{4+1}=\frac{-5units}{5}=-1unit\nonumber\]
The graph of this (constant center) of mass velocity is this simple:
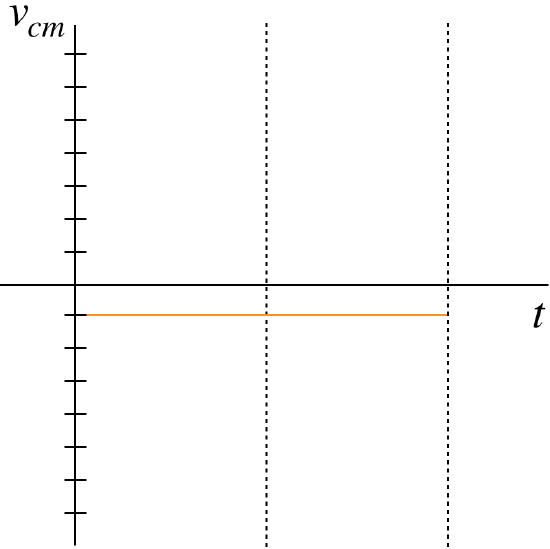
Problem 2.9
In the system shown below, the blue block remains at rest on the scale while it is attached to the pulley system as shown. All of the pulleys are massless and frictionless, and the rope is massless. In this setup, the scale reads \(980N\). The blue block is then removed from the pulleys and placed on the scale by itself, and the scale reads \(1470N\). Find the mass \(m_2\) of the orange block.
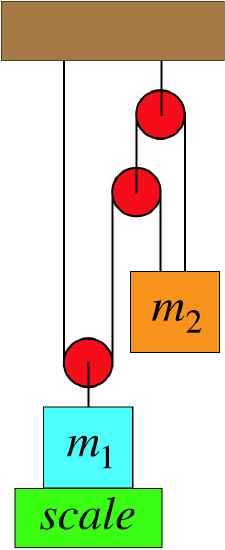
- Solution
-
In the analysis, we found:
\[N=\left(m_1-\frac{2}{3}m_2\right)g\nonumber\]
Doing some algebra to solve for what we are looking for gives:
\[m_2=\frac{3}{2}\dfrac{m_1g-N}{g}\nonumber\]
When the blue block is placed on the scale by itself, the normal force measured by the scale equals the weight of the block, \(m_1g\). Putting in this given value and the value of \(N\) when the pulleys are connected gives us the value of \(m_2\):
\[m_2=\frac{3}{2}\dfrac{1470N-980N}{9.8\frac{m}{s^2}}=75kg\nonumber\]
Problem 2.10
A rope is fastened to a block in two places and passes through a system of two massless, frictionless pulleys, as shown in the diagram below. The block rests on a rough horizontal surface. The bigger pulley can be pulled upward. It is discovered that when the strength of the pull reaches one-half the weight of the block, the block just starts to slide. Find the coefficient of static friction between the block and the horizontal surface.
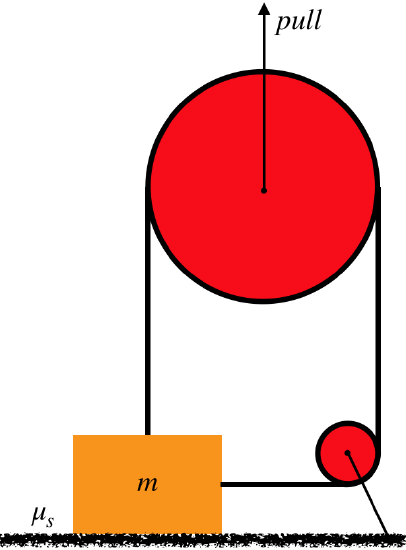
- Solution
-
The analysis gave us the relationship between the pull force, the coefficient of static friction, and the weight of the block, for the case when the friction force is maximized:
\[pull=\dfrac{2\mu_s}{1+\mu_s}mg\nonumber\]
We are given that the sliding starts when the magnitude of the pull force is one-half the weight of the block, so \(pull=\frac{1}{2}mg\). Plugging this in and solving for \(\mu_s\) gives:
\[\mu_s=0.33\nonumber\]
Problem 2.11
The system shown in the diagram below remains at rest. The rope and pulley are massless, and the pulley is frictionless, but the inclined plane is not. The coefficient of static friction is 0.35, and the blue block has twice the mass of the yellow block. Find the maximum and minimum values that \(\theta\) can have such that the system remains at rest.
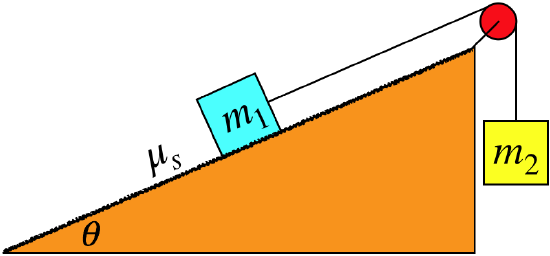
- Solution
-
We start by noting that if \(theta\) is at its extreme maximum of \(90^o\), then the normal force between the blue block and the plane is zero, resulting in zero friction force, and greater mass of \(m_1\) will cause the system to accelerate (the yellow block will rise). If \(\theta\) is at its other extreme of \(0^o\), then the plane is flat, and the maximum static friction force is just \(\mu_s=0.35\) multiplied by the weight of the blue block. But this is less than the weight of the yellow block, so the system will accelerate in the other direction (the yellow block will fall). So there must be two extremes for \(\theta\), between which the system remains at rest.
We are looking for the extreme case, so we invoke the constraint that the friction force is its maximum:
\[f_s=\mu_sN\nonumber\]
Putting this constraint together with the equations from the analysis and using the information given above that \(m_1=2m_2\) gives:
\[0=+m_1g\sin\theta+f_s-T=+m_1g\sin\theta+\mu_sN-T=+m_1g\sin\theta+\mu_sm_1g\cos\theta-m_2g\;\;\;\Rightarrow\;\;\;\sin\theta=-\mu_s\cos\theta+\frac{1}{2}\nonumber\]
We will find that this equation results in two possible values for \(\theta\). The smaller one gives a positive value for \(f_s\) (so the friction force points down the plane, as in the FBD from the analysis), and the larger one gives a negative value for \(f_s\) (indicating that the vector points up the plane, opposite to the FBD from which we derived these equations). The rest is algebra: Start by putting the equation in terms of only \(\cos\theta\):
\[\sin^2\theta=\left(-\mu_s\cos\theta+\frac{1}{2}\right)^2=\mu_s^2\cos^2\theta-\mu_s\cos\theta+\frac{1}{4}=1-\cos^2\theta\;\;\;\Rightarrow\;\;\;0=\left(\mu_s^2+1\right)\cos^2\theta-\mu_s\cos\theta-\frac{3}{4}\nonumber\]
Now solve for \(\cos\theta\) using the quadratic formula:
\[\cos\theta = \dfrac{+\mu_s\pm\sqrt{\mu_s^2-4\left(\mu_s^2+1\right)\left(-\frac{3}{4}\right)}}{2\left(\mu_s^2+1\right)}=\dfrac{+\mu_s\pm\sqrt{4\mu_s^2+3}}{2\left(\mu_s^2+1\right)}=0.988\text{ or }-0.676\nonumber\]
Taking the inverse-cosine gives these two angles:
\[\theta = 8.9^o\text{ or }132.6^o\nonumber\]
The larger of these numbers looks unusual, but it comes from the negative root of the quadratic equation, which represents the case when the frictional force points in the opposite direction than we diagrammed. We can just take the supplement of this angle (or ignore the minus sign on 0.676), and we get the more sensible answer of \(47.4^o\).
Problem 2.12
In the system shown below, the blocks are free to accelerate. All of the pulleys are massless and frictionless, and the rope is massless. The orange block starts at a height of \(8.0m\) above the blue block, and they are released from rest. After \(2.0s\), the blocks are at the same height. Find the ratio of the masses, \(\dfrac{m_2}{m_1}\).
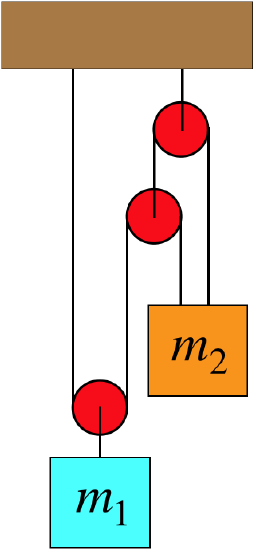
- Solution
-
We computed expressions for the accelerations of the two blocks in the analysis. We can rewrite these in terms of the ratio we are looking for:
\[a_1=\dfrac{6m_2-9m_1}{9m_1+4m_2}g=\dfrac{6\frac{m_2}{m_1}-9}{9+4\frac{m_2}{m_1}}g\;,\;\;\;\;a_2=\dfrac{6m_1-4m_2}{9m_1+4m_2}g=\dfrac{6-4\frac{m_2}{m_1}}{9+4\frac{m_2}{m_1}}g\nonumber\]
These are the rates that they are accelerating relative to the earth, but we also know that they are in opposite directions, with the blue block accelerating in the direction we chose to be positive in the FBD, and the orange block accelerating in the negative direction. So they are accelerating toward each other at a rate equal to the difference of these values. They started from rest, and we are given the distance they travel relative to each other, so we have:
\[\Delta y = \frac{1}{2}a_{rel}t^2\;\;\;\Rightarrow\;\;\;a_{rel}=\dfrac{2\Delta y}{t^2}=\dfrac{2\cdot 8.0m}{\left(2.0s\right)^2}=4.0\frac{m}{s^2}\nonumber\]
Setting the relative acceleration equal to \(a_1-a_2\) and solving for the mass ratio gives our answer:
\[4.0\frac{m}{s^2}=a_{rel}=a_1-a_2=\dfrac{10\frac{m_2}{m_1}-15}{9+4\frac{m_2}{m_1}}g\;\;\;\Rightarrow\;\;\;\dfrac{m_2}{m_1} = 2.2\nonumber\]
Problem 2.13
A rock on a string flies around in a circle (with negligible air drag) in a vertical plane (in the presence of the earth's gravity) such that it just barely gets by the top (the string remains at its full length at the top of the circle, just barely not going limp) as it continues in its circular path. The string, which has a length of \(120cm\), suddenly becomes detached from the rock at the point when the rock hits its peak, turning it into a projectile. Find how far the rock has traveled in the horizontal direction when it has fallen to a height level with the center of the circle.
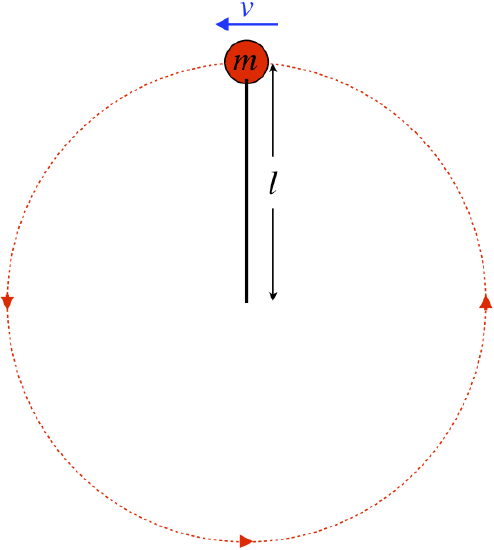
- Solution
-
We worked out the speed of the rock at the peak of the circle in the analysis: \(v=\sqrt{gl}\). When the string releases it, there is no vertical component of velocity, so we can find the time it takes the rock to fall the distance \(l\):
\[l=\frac{1}{2}gt^2\;\;\;\Rightarrow\;\;\;t=\sqrt{\dfrac{2l}{g}}\nonumber\]
With a constant horizontal component of velocity, the distance traveled horizontally is just the product of that component of velocity and the time, so:
\[\Delta x = vt=\sqrt{gl}\cdot\sqrt{\dfrac{2l}{g}}=\sqrt{2}\;l=170cm\nonumber\]


