3.3: Conservative and Non-Conservative Forces

Path-Dependence for Work

As we saw in our introduction to the work-energy theorem, the calculation of the work done by a force requires that we perform a line integral. In such an integral, the actual path that the particle takes from the start to the end is, in general, an important factor. There are some special cases, however, where the line integral calculation of the work done on a particle by a force as it moves from point A to point B results in a single, unique, value, no matter what path is taken between those points. A force that satisfies such a property is called a conservative force.  Conversely, a force for which the work done on a particle depends upon the path it takes between two endpoints is called a non-conservative force.

Another way to characterize these two types of forces is to look at the work they do to a particle that follows a closed path – a journey that begins and ends at the same position in space. Suppose a particle starts at a point A, and is moved around for awhile while acted upon by a force until it finally returns to point A. If the force is conservative, then every path that brings it back around to its starting point results in the same work done by that force. One can imagine choosing paths that are shorter and shorter until finally the "path" we try is just not moving it at all. Clearly there is no work done in this case, and if it is true for one path (however trivial), it is true for all paths. The therefore conclude:

The work done by a conservative force around any closed path is equal to zero.

This fact gives us a nice mathematical trick for recognizing conservative forces. To see the source of this trick, we will (as usual) use a simple case, which we will then be able to generalize. Consider a rectangular closed path in the \(x\)-\(y\) plane with the sides of the rectangle parallel to the \(x\) and \(y\) axes:

Figure 3.3.1 – A Simple Closed Path

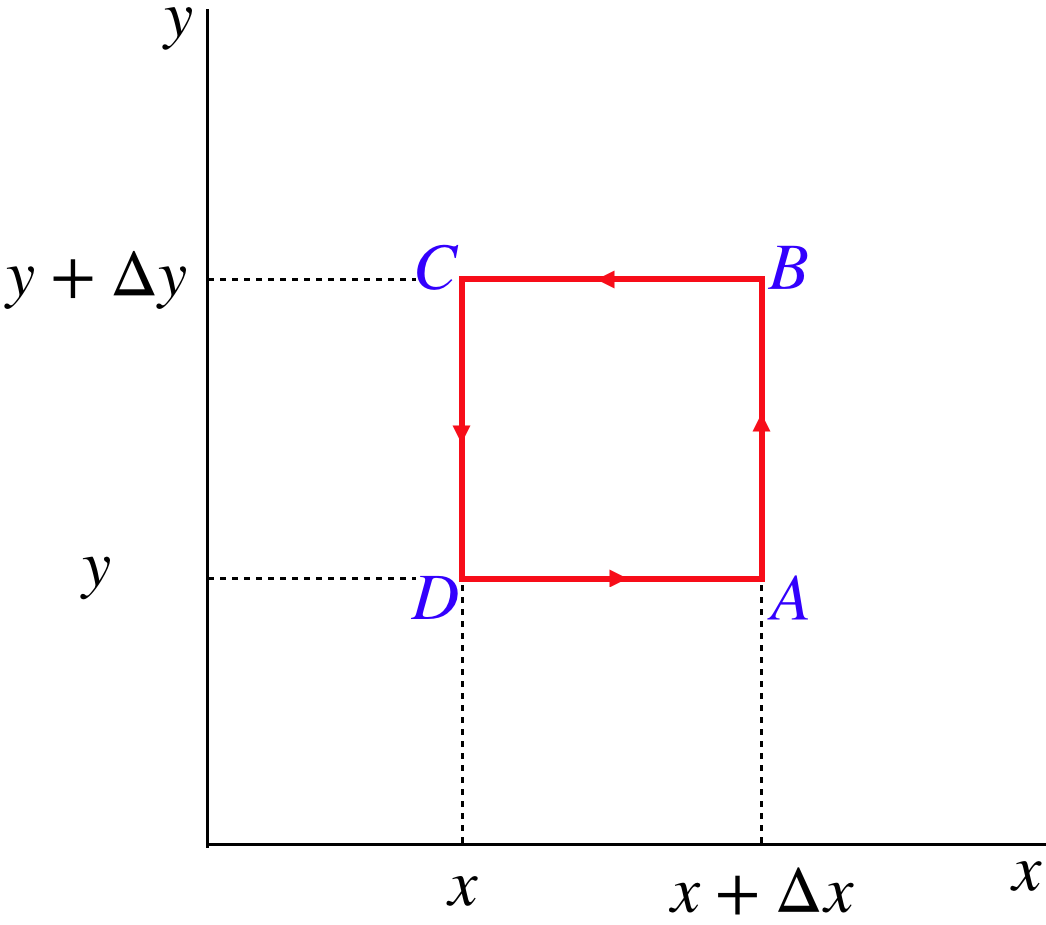
The work done by a force \(\overrightarrow F\left(x,y\right)=F_x\left(x,y\right)\;\hat i+F_y\left(x,y\right)\;\hat j\) for the part of the journey from \(A\) to \(B\) only includes the \(y\)-component of the force, evaluated at \(x\)-position \(x+\Delta x\):

\[W\left(A\rightarrow B\right) = \overrightarrow F\cdot \overrightarrow{\Delta l} = \left(F_x\;\hat i+F_y\;\hat j\right)\cdot\left(\Delta y \;\hat j\right)=F_y\left(x+\Delta x,y\right)\Delta y\]

The part of the journey from point \(C\) to \(D\) looks similar, except that the direction is negative of the \(A\rightarrow B\) path, and the force is evaluated at \(x\), rather than \(x+\Delta x\):

\[W\left(C\rightarrow D\right) = \overrightarrow F\cdot \overrightarrow{\Delta l} = \left(F_x\;\hat i+F_y\;\hat j\right)\cdot\left(-\Delta y \;\hat j\right)=-F_y\left(x,y\right)\Delta y\]

The work done over the \(B\rightarrow C\) and \(D\rightarrow A\) paths are found similarly, with the \(x\)'s and \(y\)'s swapped:

\[W\left(B\rightarrow C\right) = -F_x\left(x+\Delta x,y\right)\Delta x\;\;\;\;\; W\left(D\rightarrow A\right) = F_x\left(x,y\right)\Delta x\]

Now we add all of these contributions together to get the work done around the closed loop, and if the force is conservative, we set this equal to zero, giving:

\[0=\left[F_y\left(x+\Delta x,y\right)-F_y\left(x,y\right)\right]\Delta y - \left[F_x\left(x,y+\Delta y\right)-F_x\left(x,y\right)\right]\Delta x\]

Dividing both sides by \(\Delta x\Delta y\) gives:

\[0=\dfrac{F_y\left(x+\Delta x,y\right)-F_y\left(x,y\right)}{\Delta x}-\dfrac{F_x\left(x,y+\Delta y\right)-F_x\left(x,y\right)}{\Delta y}\]We have taken a bit of license here, when we did not concern ourselves with (for example) how the \(y\)-component of the force might change during the path \(A\rightarrow B.\) But we can remedy this by allowing the dimensions to shrink to zero, \(\Delta x\rightarrow 0\), \(\Delta y\rightarrow 0\). This turns the two terms into derivatives. More specifically, it turns them into partial derivatives. A partial derivative is a derivative that acts on a function of multiple variables (in this case, \(x\) and \(y\)), but only measures the rate of change of the function with respect to one of the variables, while holding the other one fixed. The symbols used for partial derivatives are slightly different than those for regular derivatives:

\[\dfrac{\partial f}{\partial x}\equiv\lim\limits_{\Delta x\rightarrow 0}\dfrac{f\left(x+\Delta x,y\right)-f\left(x,y\right)}{\Delta x}\]

Here's an example:

\[f\left(x,y\right)=x^2y^3 + 3y + 6x^3\;\;\;\Rightarrow\;\;\;\dfrac{\partial f}{\partial x} = 2xy^3+0+18x^2\;,\;\;\;\;\dfrac{\partial f}{\partial y} = 3x^2y^2+3+0\]

The condition we have for a force \(\overrightarrow F\left(x,y\right)=F_x\left(x,y\right)\;\hat i+F_y\left(x,y\right)\;\hat j\) to be conservative is therefore most compactly written as:

\[0=\dfrac{\partial F_y}{\partial x}-\dfrac{\partial F_x}{\partial y}\]

If the force has components in three dimensions, then of course this mathematical condition has to also apply to the \(y\)-\(z\) and \(x\)-\(z\) planes as well.

Digression: Curl

While it is beyond the scope of this course, a reader with more mathematical background than required for this class may recognize this condition for a conservative force as being the zero "curl" of the force vector field:

\[\text{curl of }\overrightarrow F\left(x,y,z\right)=\overrightarrow\nabla\times\overrightarrow F\equiv\left| \begin{array}{c}\hat i && \hat j && \hat k \\ \dfrac{\partial}{\partial x} && \dfrac{\partial}{\partial y} && \dfrac{\partial}{\partial z} \\ F_x && F_y && Fz \end{array}\right| = \left(\dfrac{\partial F_z}{\partial y}-\dfrac{\partial F_y}{\partial z}\right)\hat i + \left(\dfrac{\partial F_x}{\partial z}-\dfrac{\partial F_z}{\partial x}\right)\hat y + \left(\dfrac{\partial F_x}{\partial y}-\dfrac{\partial F_y}{\partial x}\right)\hat k=0\nonumber\]

Analyze This

Consider the following forces that act on a particle as it moves in the \(\left(x,y\right)\) plane (\(\alpha\) is a constant):

• \(\overrightarrow F\left(x,y\right)=\alpha\left(x \;\hat i-y \;\hat j\right)\)
• \(\overrightarrow F\left(x,y\right)=\alpha\left(y \;\hat i-x \;\hat j\right)\)

Analysis

There are a few ways we can check whether this force is conservative or not. The simplest involves taking the partial derivatives of the components of the force:

\(\overrightarrow F\left(x,y\right)=\alpha\left(x \;\hat i-y \;\hat j\right)\) :

\[\dfrac{\partial}{\partial x}F_y=\dfrac{\partial}{\partial x}\left(-\alpha y\right)=0\nonumber\]

\[\dfrac{\partial}{\partial y}F_x=\dfrac{\partial}{\partial y}\left(\alpha x\right)=0\nonumber\]

With both of these derivatives vanishing, our check confirms that this force is conservative:

\[\dfrac{\partial F_y}{\partial x}-\dfrac{\partial F_x}{\partial y}=0-0=0\nonumber\]

\(\overrightarrow F\left(x,y\right)=\alpha\left(y \;\hat i-x \;\hat j\right)\) :

\[\dfrac{\partial}{\partial x}F_y=\dfrac{\partial}{\partial x}\left(-\alpha x\right)=-\alpha\nonumber\]

\[\dfrac{\partial}{\partial y}F_x=\dfrac{\partial}{\partial y}\left(\alpha y\right)=\alpha \nonumber\]

For this case, our check shows that the force is non-conservative:

\[\dfrac{\partial F_y}{\partial x}-\dfrac{\partial F_x}{\partial y}=-\alpha-\alpha=-2\alpha\ne 0\nonumber\]

Another method would be to perform a work integral between two points over different paths. Unfortunately, this method will only work as a proof that the force is non-conservative if the two integrals come out different. If the two integrals come out the same, it does not prove that the force is conservative, since those two paths could coincidentally result in the same work for a non-conservative force. As we cannot perform the work integral for all paths, we can't use that method to conclusively prove that the force is conservative.

 Examples of Conservative Forces

Let's look at a few important examples of conservative forces.

central forces

The first is very fundamental to all of physics, and it goes like this:

Any force on a particle that originates from a single point is conservative.

This can be proven mathematically with the tools we have, but we will refrain from doing so here. The way this is usually expressed by physicists is, "central forces are conservative,"  where a central force is one that originates from a single point (the "center"). Reminding ourselves that forces are interactions between two objects, a force that "originates" from a single point is one that is exerted by an object located at that single point. Put another way, this is a force from another particle! We labeled forces that act between individual particles as "fundamental forces," so we therefore conclude that all fundamental forces are conservative.

Digression: Spherical Sources

While all forces that have point particles as a source are certainly central forces, the converse is not true. It is possible to have a central force whose source is a collection of particles, if those particles are placed very symmetrically – in the shape of a sphere. This fact will become important later when we get to gravitation, because stars and planets very closely approximate spheres, which means we can treat the gravitational forces they exert as conservative to a very good approximation.

This means that to the extent that we see non-conservative forces in nature, the source of its non-conservative nature must be that the forces are exerted by objects that are collections of particles rather than by individual particles. This is not to say that the composite forces we have discussed (gravity, elastic, drag, etc.) are inherently non-conservative. It just means that they require just the right conditions to be "considered" conservative to a good approximation.

Alert

Resist the temptation to label a certain type of force as either conservative or non-conservative. One cannot tell whether a type (gravity, tension, etc.) is conservative or not without more details of how this type of force is acting. It is perhaps better not to say that a given force is conservative, and instead say that the force is "being applied in a conservative manner." But this is not the language you will find elsewhere, so we will not use it here.

gravity

As a composite force, we have approximated gravity as a constant force at all points in space – we assume that the region involved is small compared to the size of the Earth. Subject to the limits of this approximation, we can declare gravity to be conservative:

\[\overrightarrow F_{grav}=-mg\;\hat j\;\;\;\Rightarrow\;\;\; \dfrac{\partial F_y}{\partial x}-\dfrac{\partial F_x}{\partial y}=\dfrac{\partial}{\partial x}\left(mg\right)-\dfrac{\partial}{\partial y}\left(0\right)=0\]

It is enlightening to look at how much work is actually done by gravity as a particle moves around. The work done by gravity on a particle that moves from point \(A\) to point \(B\) (near the surface of the Earth, of course) is given by:

\[W\left(A\rightarrow B\right) = \int\limits_{A\rightarrow B}\overrightarrow F_{grav}\cdot\overrightarrow{dl}\]

As usual, we have  that \(\overrightarrow{dl}=dx\;\hat i+dy\;\hat j\), but as we will see, we will be able to determine the work done without specifying a path from \(A\) to \(B\) by expressing \(y\) as a function of \(x\):

\[W\left(A\rightarrow B\right) = \int\limits_A^B\left(-mg\;\hat j\right)\cdot\left(dx\;\hat i+dy\;\hat j\right)=-mg\left(y_B-y_A\right)\]

The work done by gravity depends only upon the change in height of the particle. It is important to note a few things about this result:

• It doesn't depend upon the path taken from the starting height to the ending height – it could go straight up, or take many loop-de-loops that go above and below the starting and ending points, and the result is the same.
• The actual value of the starting and ending heights are not relevant, it is only the difference of the starting and ending heights that matters.
• According to the work-energy theorem, if gravity is the only force that does work on a particle (or if other forces that might be acting happen to cancel out), then the change of kinetic energy of a particle (and therefore its speed) can be calculated using nothing more than the change in the particle's height.

Exercise

A particle follows projectile motion free of air resistance. According to the work-energy theorem, its change in kinetic energy equals the work done on it by the net force, which in this case is only gravity, so:

\[W_{grav}=\Delta KE\;\;\;\Rightarrow\;\;\;-mg\Delta y=\Delta\left(\frac{1}{2}mv^2\right)\nonumber\]

Confirm that this is true using tools we have from kinematics.

Solution

We will assume that the particle travels from point A to point B. For projectile motion, the \(x\)-component of velocity doesn't change, which means that:

\[v_{Ax}=v_{Bx}\nonumber\]

The \(y\)-component does change, and since we know nothing about how long the particle is in the air, we will use the "no time equation" for vertical motion accelerated by gravity (\(a_y=-g\)):

\[v_{By}^2-v_{Ay}^2=2\left(-g\right)\left(y_B-y_A\right)\nonumber\]

Using the result of the first equation, we can add \(0=v_{Ax}^2-v_{Bx}^2\) to the left side of this equation without changing it, giving

\[\left(v_{Bx}^2+v_{By}^2\right)-\left(v_{Ax}^2+v_{Ay}^2\right)=-2g\left(y_B-y_A\right)\nonumber\]

The quantities in parentheses are just the squares of the speeds at points \(B\) and \(A\), respectively, so:

\[v_B^2-v_A^2=2g\left(y_B-y_A\right)\;\;\;\Rightarrow\;\;\;\Delta \left(v^2\right) = -2g\Delta y\nonumber\]

Now multiplying both sides by the mass of the particle and dividing both sides by 2 reconstructs the work-energy theorem result given above.

Analyze This

A small block slides along a frictionless, horizontal surface into a frictionless vertical half-circle track, and it remains in contact with the track, until at least the \(\theta=90^o\) point (with \(\theta\) defined in the diagram).

Analysis

With no friction present, the only forces acting on the block are gravity and the normal force. We can ask how much work each of these forces do on the block. We assume the gravitational force is a constant \(mg\) downward, so from our efforts above, we conclude that the work done by gravity is:

\[W_{grav}=-mg\Delta y\nonumber\]

If we call the radius of the circle \(R\), then we can express the change in the height in terms of \(R\) and \(\theta\):

\[W_{grav}=-mgR\left[1+\sin\left(\theta-90^o\right)\right]=-mgR\left[1-\cos\theta\right]\nonumber\]

The work done by the normal force might seem complicated at first, since on the curved track it is constantly changing direction, but every infinitesimal displacement by the block \(\overrightarrow {dl}\) is parallel to the track, while the normal force is always perpendicular to the track. Each contribution to the work done is \(dW=\overrightarrow N\cdot\overrightarrow {dl}\), and since the normal force and displacement are perpendicular to each other at all times the work done by this force is zero.

Now that we know the total work done by all forces, we can apply the work-energy theorem to get the speed of the block after it climbs the angle \(\theta\):

\[\frac{1}{2}mv_f^2-\frac{1}{2}mv_o^2=-mgR\left(1-\cos\theta\right)\;\;\;\Rightarrow\;\;\;v_f=\sqrt{v_o^2-2gR\left(1-\cos\theta\right)}\nonumber\]

There is one other thing that we can extract from this analysis. We know that the block is still in contact with the track when it reaches the angle \(\theta\). It has been slowing down as it gets higher, so the centripetal acceleration \(\dfrac{v^2}{R}\) that keeps it going in a circle has gotten smaller, but it is not zero. The normal force combined with a component of the gravity force is what is maintaining this acceleration, and as it goes higher from its current position, the component of the gravity force acting toward the center of the circle will get larger. So this means that the decaying centripetal acceleration is due to a decreasing normal force. The normal force can only go to zero (it can't become negative), and if it does, then the block will start to lose contact with the track. We can therefore determine the minimum speed the block must have at angle \(\theta\) to maintain contact with the track (anything less, and it falls off). The gravity force can be broken into components radial (toward the center of the circle) and tangential to the track (use a FBD and geometry to determine these components), and setting the normal force equal to zero gives:

\[N-mg\cos\theta=m\dfrac{v^2}{R}\;\;\;\Rightarrow\;\;\;v_{min}=\sqrt{-gR\cos\theta}\nonumber\]

[Note that the minus sign is present because angle being used (the cosine of \(\theta>90^o\) is negative).]

elastic

In one way, the elastic force is an even easier case than that of gravity – the particle's displacement is entirely confined to one dimension. But it does include the twist that unlike gravity, it does not maintain a constant magnitude. Let's define the one dimension we are working in to be the \(x\)-axis. Let's further assume that the particle that is subject to the elastic force experiences zero force when it is located at \(x=x_o\). That is, when the particle is here, then the spring is at its equilibrium length. Then according to Hooke's law, the force on the particle is:

\[\overrightarrow F_{elastic} =-k\left(x-x_o\right)\hat i\]

When the particle is located in the region \(x>x_o\) it experiences a force in the \(-x\)-direction (back toward \(x_o\)), and when it is in the region \(x<x_o\), it experiences a force in the \(+x\)-direction (also back toward \(x_o\)). So this is the restoring force we expect for the elastic force. The partial derivative check once again demonstrates that this is a conservative force. As with the case of gravity, we can compute the work done by the spring on the particle. All the displacements in this case are confined to the \(x\)-axis, so we have simply that \(\overrightarrow{dl}=dx\;\hat i\), giving:

\[W\left(A\rightarrow B\right) = \int\limits_{A\rightarrow B}\overrightarrow F_{elastic}\cdot\overrightarrow{dl}= \int\limits_A^B\left[-k\left(x-x_o\right)\hat i\right]\cdot\left(dx\;\hat i \right)=\left[-\frac{1}{2}kx^2+kx_ox\right]_{x_A}^{x_B}=-\frac{1}{2}k\Delta\left(x^2\right)+kx_o\Delta x\]

We can simplify the look of this result a bit by defining the equilibrium point of the spring to be the origin \(x_o=0\), giving:

\[W\left(A\rightarrow B\right) = -\frac{1}{2}k\Delta \left(x^2\right)\]

We see that this result differs from that of gravity, in that the work done by gravity is proportional to how much the (vertical) position changes, while the work done by the elastic force is proportional to how much the square of the position changes. So if one particle changes its height by twice as much as another particle, gravity does twice as much work on it. But if a particle changes its position from the equilibrium point twice as much as another particle, the spring does four times as much work on it.

We have been careful to define all of these conservative forces in terms of the displacement of a particle, rather than an "object." But just as we saw in earlier sections, we can extend these results to non-rotating objects whose constituent particles remain rigidly in place within the object. If they do not, then an object that follows a closed path may end up with a different internal energy, which can have an effect on the amount of kinetic energy it has. And if the kinetic energy changes around a closed path, then the work done around that closed path is not zero, and the force on that object is not conservative.

Analyze This

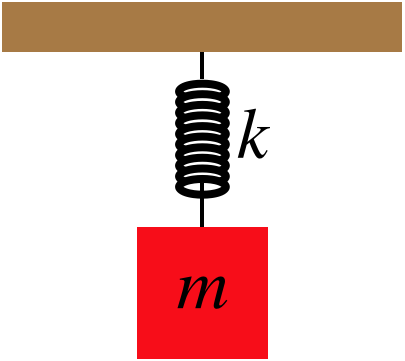
A block is attached to a vertical spring, the other end of which is attached to the ceiling. The block is held stationary at a height where the spring is at its equilibrium length. The block is then released.

Analysis

There are two forces acting on the block when it is released. One is the force of gravity downward, and the other is the elastic force of the spring upward. Both of these conservative forces do work at the same time on the block, and since the block moves downward, the gravity force (which acts in the direction of motion) does positive work, while the elastic force (which acts opposite to the direction of motion does negative work.

One thing we can determine, if given all the numbers, is how far the block will fall before stopping and bouncing back up. If we are careless, we might conclude too quickly that this must be where the two forces cancel each other out – but this is wrong! As the block is falling, when it reaches the point where the forces cancel, then the net force is zero, which means it stops accelerating. This does not mean it stops moving.

The way we find the distance it falls before stopping is to use the work-energy theorem. The total work done by all forces equals the change in kinetic energy. The kinetic energy starts at zero, and we are interested in where the block once again has zero kinetic energy – when it stops falling. As stated above, gravity does positive work as the block falls, and the spring does negative work, so we are looking for the distance where these cancel out to give zero total work. Calling the stretch of the spring from equilibrium at the point where the block stops \(+\Delta y\), then the change of the block's height is \(-\Delta y\), and we can use the work results for the gravity and elastic forces above to get:

\[0=W_{tot}=W_{spring}+W_{grav}=\left[-\frac{1}{2}k\left(\Delta y\right)^2\right]+\left[-mg\left(-\Delta y\right)\right]\;\;\;\Rightarrow\;\;\;\Delta y = \frac{2mg}{k}\nonumber\]

The solution also included the possibility that \(\Delta y=0\) – naturally no total work is done if the block never moves, or (since the forces are conservative) if it comes back to the position where it started.

Also notice that if the block was hung stationary from the spring, then the forces would balance, giving \(k\Delta y = mg\). The value of \(\Delta y\) in this case is half as much as that found above. So the zero-net-force position is exactly halfway between the maximum and minimum heights of the block.

Now for Some Non-Conservative Forces

Next we will discuss a couple of non-conservative forces. The first is fairly obvious, but the second may be surprising.

kinetic friction

The kinetic friction force is quite unlike the others we have discussed. It's magnitude is simple enough – if the normal force and the surfaces remain unchanged, then the kinetic friction is constant – but the direction is quite another matter. The kinetic friction force on one object always acts in the direction opposite to the direction of motion of that object relative to the surface it is rubbing against. Consider a hockey puck sliding on a horizontal table. If it is sliding north when it is located at point \(\left(x,y\right)\), then the friction force points south. If, at a later time, it is sliding east at that same point \(\left(x,y\right)\), then the direction of the friction force points west. What this tells us is that the direction of the force cannot be determined from the location alone – one must know the direction of motion.

If we now look back at our partial derivative formula for determining whether a force is conservative, it requires that we know the \(x\) and \(y\) components of the force as a function of the position \(\left(x,y\right)\). We cannot get this information in the case of kinetic friction. The partial derivative equation is both a necessary and sufficient condition for the force to be conservative, so when it is unusable for a given force, that force is necessarily non-conservative.

Perhaps this is an unsatisfying explanation. Fair enough, let's do a more rigorous analysis of the case of kinetic friction for a specific case:

Analyze This

A puck is slid along a horizontal rough surface in a straight line along the diameter of a circle (the gravity, contact and friction forces are the only forces on the puck).  The same puck is then slid on the same surface starting at the same speed along the circle defined by the diameter indicated in the first experiment (it slides around the inside surface of a frictionless circular wall). The figure shown depicts a top view of these two paths.

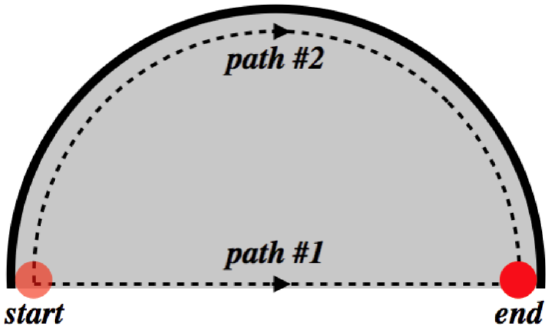
Solution

The kinetic friction force always acts in the direction directly opposite to the motion. So for every small displacement \(\overrightarrow{dl}\) along the path taken, the direction of the friction force is always the same as the direction of \(-\overrightarrow{dl}\). When we compute the work done by friction, we therefore have:

\[dW=\overrightarrow f_k\cdot\overrightarrow{dl}=\left|\overrightarrow f_k\right|\left|\overrightarrow{dl}\right|\cos180^o=-f_kdl\nonumber\]

The magnitude of the kinetic friction force is constant, as it is proportional to the unchanging normal force (the surface remains horizontal). So the line integral can pull the constant \(f_k\) out of the integral, leaving:

\[W\left(A\rightarrow B\right)=-\int\limits_A^B f_kdl=f_k\int\limits_A^B dl = -f_k\left(\text{length of path}\right)\nonumber\]

The length of the path that follows a half-circle path (#2) is longer than the straight-line path (#1) by a factor of \(\frac{\pi}{2}\), so the work done on the puck by friction is greater (more negative) for path #2 than for path #1 by that factor.

Notice that both paths begin and end at the same points, but the work done is different for the two paths, demonstrating that kinetic friction is non-conservative.

One might ask, "The frictional force between the particles on the surfaces is ultimately electric, which is a fundamental force, and therefore conservative, so what is the physical source of this force being non-conservative?" The answer is that by only interacting at their surfaces, some particles in the rubbing objects are accelerated while others are not. This results in changes in the internal energies of the rubbing objects. In the analysis example above, path #1 results in less energy being transferred into internal energy than path #2 (more surface particles are affected in the longer path). With the internal energies changed by different amounts, the kinetic energies change by different amounts. This can only occur if different amounts of work are performed, and since the two paths begin and end at the same place, and by definition this means that the force is non-conservative.

gravity

Wait... gravity? Didn't we just learn that gravity is a conservative force? Gravitation as a force between individual particles is conservative as all fundamental forces are, and gravity near the surface of the Earth is approximately constant, making it approximately conservative, but here we are going to look at an example where this force does not behave as a conservative force.

The Voyager probes were launched in 1977. Neither was given sufficient kinetic energy to escape the Sun's gravitational pull without "help." If we approximate a probe and the sun as individual particles (when they are far apart, this is reasonable), then when the gravitational pull of the Sun brings the probe back to the point where it began, no net work will be done, and the probe's kinetic energy goes back to its starting value. Now let's introduce a third particle – Jupiter. We will declare the Sun and Jupiter to be a two-particle object (we'll call it the "solar system"), and examine what can happen to the individual Voyager "particle" when it interacts with this system.

Some very bright minds at NASA launched the Voyager probes so that they would get gravitational "kicks" from flying close to planets, the result of which is increased speed for the Voyager probes that is sufficient to escape the Sun's gravitational pull. Now suppose NASA made a small miscalculation, and sent the probe (with its extra gravitational kick) back toward the Sun, instead of away from it. Then when it returns to the point where it started, it is moving faster than when it was launched. This means that the starting and ending kinetic energies at the same point in space are not equal, and the force on the probe by the solar system is not conservative. [If you are curious about how this gravitational "kick" is accomplished, see the simplified explanation at the end of Section 7.3.]

As with the case of friction, this result comes about because the force on the particle comes from different parts of the system acting independently, and those different parts moving relative to each other (as Jupiter moves around the Sun). The Sun and Jupiter "particles" each exert their own conservative gravitational force on the probe, and the aggregate of these forces comes out to be non-conservative.