4.3: Momenta of Systems

Using Momentum Conservation

When we examined the work-energy theorem, we found that it was not much more than a reformulation of Newton's 2nd Law for cases where we are only interested in speed (not direction) changes. As such, it had only limited usefulness. But when we went a little deeper, we found that this theorem spawned a very useful "shortcut" (the principle of energy conservation) that allowed us to solve certain types of problems much more easily than we could otherwise. We have already expressed a conservation principle for momentum, but let's do so again here, comparing it to the familiar counterpart in energy.

Energy: In isolated system (one where there is not external work being done on any of the objects in it), the total energy of the system remains constant.

\[ \underbrace{KE+PE+E_{thermal}}_\text{before} = \underbrace{KE+PE+E_{thermal}}_\text{after} \]

Momentum: In isolated system (one where there is not external impulse delivered to any of the objects in it), the total (vector) momentum of the system remains constant.

\[ \vec p_{cm}\left(\text{before}\right) = \vec p_{cm}\left(\text{after}\right) \;\;\;\Rightarrow\;\;\;\underbrace{\vec p_1+\vec p_2+\dots}_{\text{before}} = \underbrace{\vec p_1+\vec p_2+\dots}_{\text{after}}\]

The sum on each side is over the several objects in the system. So adding up the momentum vectors of all the objects before some event, and then doing it again after the event gives the same vector. This of course assumes that the "event" does not involve an external impulse, though it can include as many internal impulses as you like.

Alert

It is important to remember that this equation does not mean that each of the terms remains unchanged. Rather, they change in such a way that the changes all compensate for each other, and the vector sum of the all-new momentum vectors comes out to the same that came out before.

Analyze This

A child sits on the rear end of a sled (whose mass is uniformly-distributed along its length) with a block of frozen snow at rest in her lap. The sled is sliding forward on the horizontal, frictionless snow at constant a speed, when the child suddenly shoves the block forward in the sled (she remains firmly planted on the sled). After a period of time, the block comes to rest in the front of the sled.

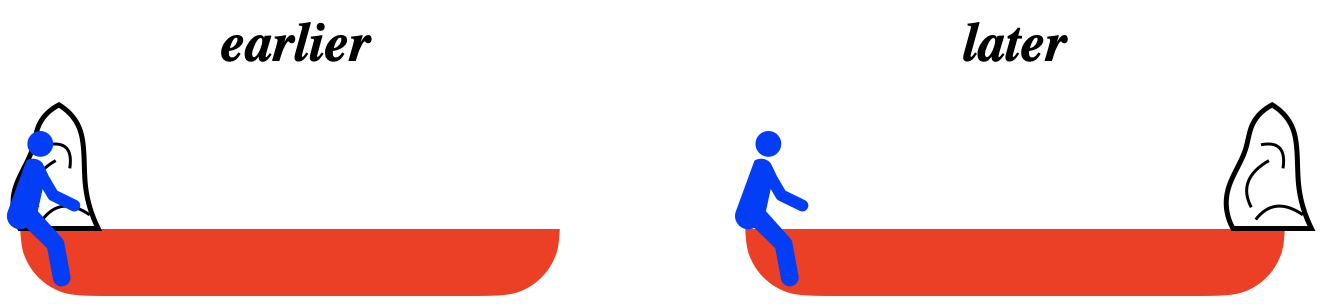
Analysis

The forces between the girl, the block of snow, and the sled are all internal to that system of those three objects. With no friction coming from the snow, this means that there are no external forces on this system, and its total momentum remains unchanged. This means that the center of mass of the system of the child, the sled, and the ice, continues sliding at the same constant rate as before. This does not mean that the sled+child combination slides at the same rate throughout this process, because the increased speed of the ice means that the remaining mass of the system must change speed to keep the center of mass speed unchanged.

Once the ice reaches the front of the sled, however, the whole system is moving at the same speed again, which means that it returns to the speed it had before the ice was pushed. Without knowing the masses of the parts of this system, we don't know the specific effect of the sliding ice – it could just slow the sled+child, stop the sled+child, or even cause them to move backward. The graph of speeds as a function of time below expresses this well:

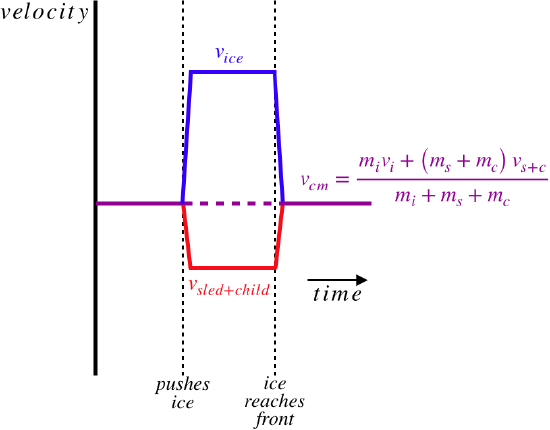
A few things to note here:

• The graph assumes that the mass of the sled+child is greater than the mass of the ice, because the internal force between them delivers the same impulse to both, which means that they change their momenta by the same amount. The graph shows the speed of the ice changing more, so to experience the same change of momentum, it must have less mass.
• Even though the ice and sled+child have different speeds for a short period of time, even during that time, the speed of the center of mass doesn't change (depicted by the dotted purple line).
• We don't know the actual speeds, so we can't place the time axis on the graph. If it happens to coincide with the horizontal red line segment, then the sled+child come to rest while the ice slides forward. If the time axis is above this horizontal red line (it must be below the purple line, as we have defined the starting velocity to be in the positive direction), then the sled+child actually moves backward while the ice slides forward.

Using Center of Mass

Let's look at an example of how we can use what we know about center of mass the analyze a case of two blocks of different masses that squeeze a (massless) spring between them until they are released from rest.

Figure 4.3.1 – Repelling Masses

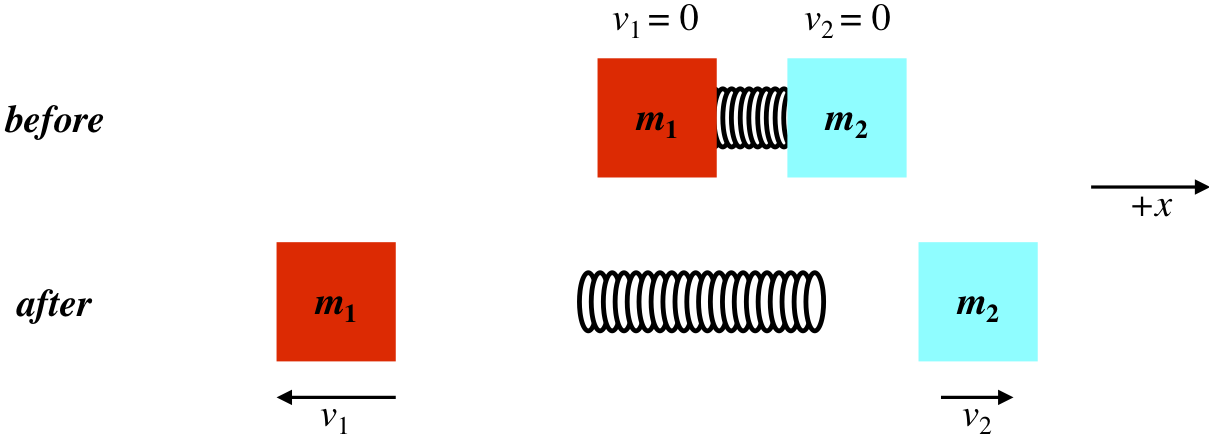
Intuitively one can probably tell that for this situation \(m_2>m_1\). When a light object pushes off a heavy one (a flea jumping off a dog, a bullet leaving a gun, etc.), the lighter object's motion is always affected more. With our physics training, we can explain it with Newton's second and third laws: The blocks push on each other with equal forces (third law), and with equal forces, the block with less mass will accelerate more. They both start from rest and are pushed for equal periods of time, so the one with the greater acceleration will be going faster when they separate, sending it a greater distance in the same time period.

Okay, now let's look at it from the perspective of momentum conservation. Treating the two blocks as a single system, the spring force produces only internal impulses, which means that the momentum of the system is conserved. The momentum before the spring unloads is zero, so it must be zero afterward. If \(v_1\) and \(v_2\) are the speeds of the two blocks (i.e. these are positive numbers), then we have for our conservation equation:

\[ \text{momentum before} = \text{momentum after} \;\;\; \Rightarrow \;\;\; 0 = m_1 v_1 \left(- \widehat i \right) + m_2 v_2 \left(+ \widehat i \right) \;\;\; \Rightarrow \;\;\; v_1 = \dfrac{m_2}{m_1} v_2 \]Since it's clear from the diagram that \(v_1>v_2\), it must be that \(m_2>m_1\). We can also use what we know about center of mass here. The system experiences no external net impulse and its center of mass is stationary, so it must remain stationary! We don't know exactly where the center of mass is before the repulsion, but since it stays put, we can draw a vertical line down into the second diagram to find where it is after the repulsion. This clearly results in the center of mass being closer to \(m_2\), which means that is the larger mass.Center of Mass Acceleration

Let's see if we can incorporate what we have learned about center of mass to make sense of Newton's second law. Consider the two systems shown in Figure 4.3.2. Each consists of a collection of 8 identical particles in close proximity to each other (the boxes shown are just used as a reference for later motion – they are not physical objects). In the left system, the particles are floating freely (there is no gravity or other forces), while in the right diagram, the particles are bound together with rigid, massless rods. The two systems are identical in every way except for the presence of these rods – the particle all have the same positions and masses as their counterparts, and are all at rest.

Now for the experiment: Suppose we exert the same force on the same particle in both systems. Clearly the reaction is different in the two cases – in the left case, only the particle given the push accelerates away, while in the right cases the entire group of particles accelerates. The question is, in which case does the center of mass of the system of particles accelerate more?

Figure 4.3.2 – Forces on Free and Rigid Systems

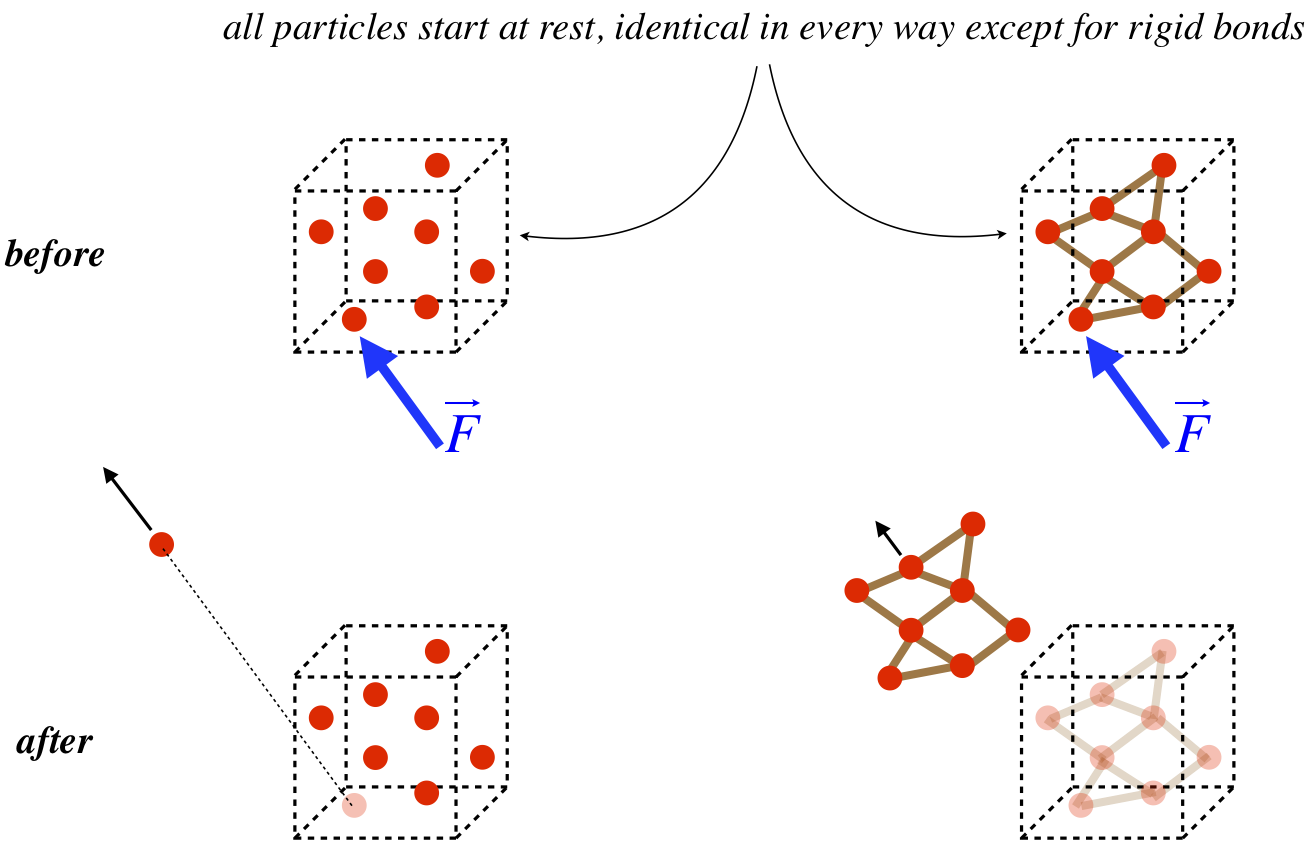
Here is the short answer: The forces that are (or are not) between the particles defining the system are internal, and therefore have no effect on the velocity of the system's center of mass. The only external force on each system is \(\overrightarrow F\), and each system has the same mass, so Newton's second law says that both systems should react with the same acceleration of their center of mass.

But that is unconvincing when we see only one particle move in one case, and the whole conglomerate move in the other! Let's suppose the forces act for some small period of time. The acceleration of the single particle will be eight times greater than that of the conglomerate, so in the same time interval it will move eight times as far as the conglomerate. Let's call the initial position of the center of mass the origin. The seven particles left behind experience no change in their position relative to this origin, and the one particle's position relative to the origin travels eight units of distance, while all eight of the particles in the other system travel just one unit from their original positions relative to the origin. Treating the direction of motion as the \(+x\) direction, and plugging the masses and distances into Equation 4.2.1, it should be immediately clear that both centers of mass move by the same amount. As strange as it sounds, Newton's second law works for any system of particles, whether they bond together to form a solid object, or are completely independent of each other, like particles in a gas.

Conceptual Question

A system of four balls of varying relative masses is shown in the left diagram below, and there is a force exerted on one of the balls as indicated. In the right diagram are a few options for other forces that can be exerted on balls in this system.  Which of these forces will assure that the center of mass of this system does not accelerate?  The forces shown are the only forces present (i.e. there is no gravity or other forces to worry about here).

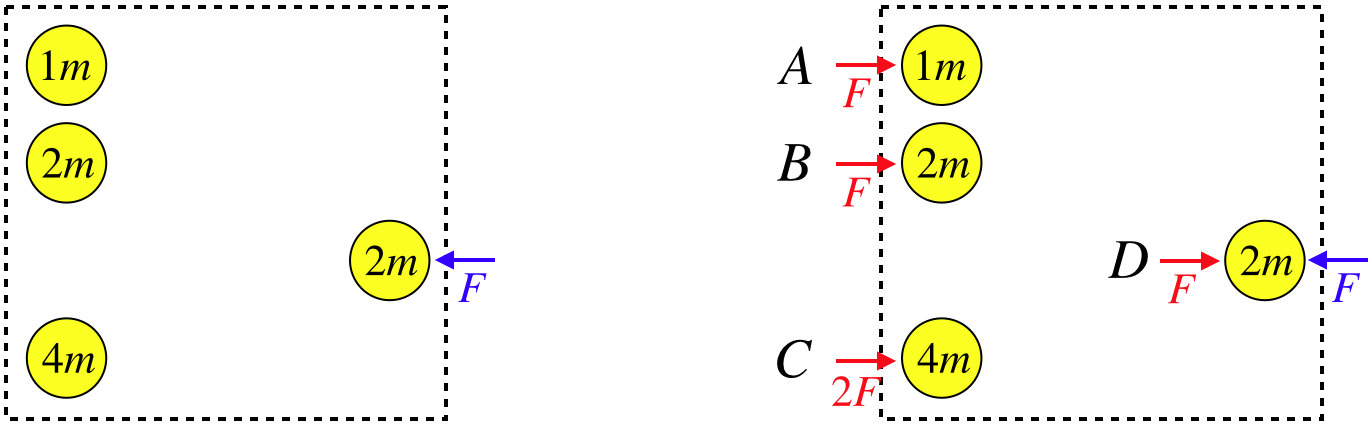
1. D only
2. B or D only
3. B, C, or D only
4. A, B, or D only
5. There needs to be a force \(F\) exerted to the right on every ball at at the same time.

Solution

d

For the center of mass to not accelerate, the net force on the system must be zero. This means that a force must be applied to the system in the opposite direction. It doesn’t matter where in the system this force is applied.

Analyze This

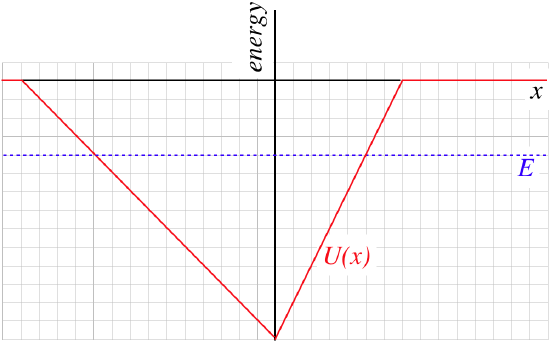
Two different particles are confined by the same potential, shown in the diagram.  Both particles have the same total energy, also depicted in the diagram.  At one moment the particles pass each other precisely at the origin, with one particle moving in the \(-x\)-direction and the other moving in the \(+x\)-direction.

Analysis

There is a lot unpack here. We'll start by labeling the particles: The particle moving in the \(-x\) direction we'll call "particle A", and the one moving the other way "particle B". Clearly at the moment that they cross each other at the origin, the center of mass is at the origin. But does it remain there as they continue moving away from each other?

To answer this question, we consider the net force on the two particle system. If it is zero, then the center of mass does not accelerate. The system experiences two forces, one on each particle. These forces can be computed from the slope of the potential energy function \(U\left(x\right)\). The left side of the potential curve affects particle A (pushing it in the \(+x\)-direction), and the right side affects particle B (pushing it in the \(-x\)-direction). The slopes of the two sides are not equal, so the forces on the particles are not equal, which means that there is in fact a net force on the two-particle system, and the center of mass is accelerating. With more force being applied in the \(-x\)-direction, the center of mass is accelerating in that direction. We even have enough information to determine the ratio of these two forces, thanks to the grid lines:

\[\left.\begin{array}{l}\text{force on particle A}=F_A=-\text{slope of left segment} = 1\;unit \\ \text{force on particle B}=F_B=-\text{slope of right segment} = -2\;units \end{array}\right\}\;\;\;\left|\frac{F_B}{F_A}\right|=2\nonumber\]

Does this mean that a short time later the center of mass is on the \(-x\) side of the origin? No! We don't know which way the center of mass is moving when it is at the origin. If it is stationary or moving in the \(-x\)-direction, then of course the center of mass speed is increasing in the \(-x\)-direction and the center of mass will later be on the \(-x\) side. But the center of mass may be moving in the \(+x\)-direction, which would mean that it is slowing down, but will still be on the \(+x\) side a short time later.

Is there any way to know the direction of the center of mass motion when both particles are at the origin? Another way to ask this is, in which direction is the momentum of the system? One thing we do know is that both particles have the same total energy, and when they are both at the origin, they have the same potential energy as well. This means that at the moment they pass each other, they have equal kinetic energies. We know a relationship between kinetic energy (Equation 4.1.6):

\[KE=\frac{p^2}{2m}\;\;\;\Rightarrow\;\;\;p=\sqrt{2m(KE)}\nonumber\]

With both particles having the same kinetic energy, the particle with more mass is the one with more momentum, and when these momenta are summed, the direction of motion of the particle with more mass is the direction in which the center of mass is moving.

Center of Mass Frame

Sometimes analysis of problems that involve multiple objects interacting with each other is simplified by using what is called the center of mass frame of reference. Here’s an example.

A child's toy called a "hot potato" consists of two hemispherical shells that close on a spring and are held together by a latch on a timer. When the time expires, the latch is released and the spring is allowed to expand, shooting the two shells in opposite directions, exposing the toy company to a product liability lawsuit from the family of the child that holds the hot potato when it goes off.

Let's suppose a child throws this hot potato through the air, and the peak of its projectile motion, it explodes so that the two shells are propelled horizontally, as shown in Figure 4.3.3. The landing point of the shell that lands closest to where the toy was thrown is noted, but the other shell flies off into some tall grass and is lost. Naturally the child knows the starting speed they gave the toy as well as the exit angle, and she can easily measure the distance that the closer shell travels form the launch point. From this information and her vast knowledge of physics, she conceives of a plan to find the other shell that is far more elegant than searching for it in the tall grass.

Figure 4.3.3 – Exploding Projectile

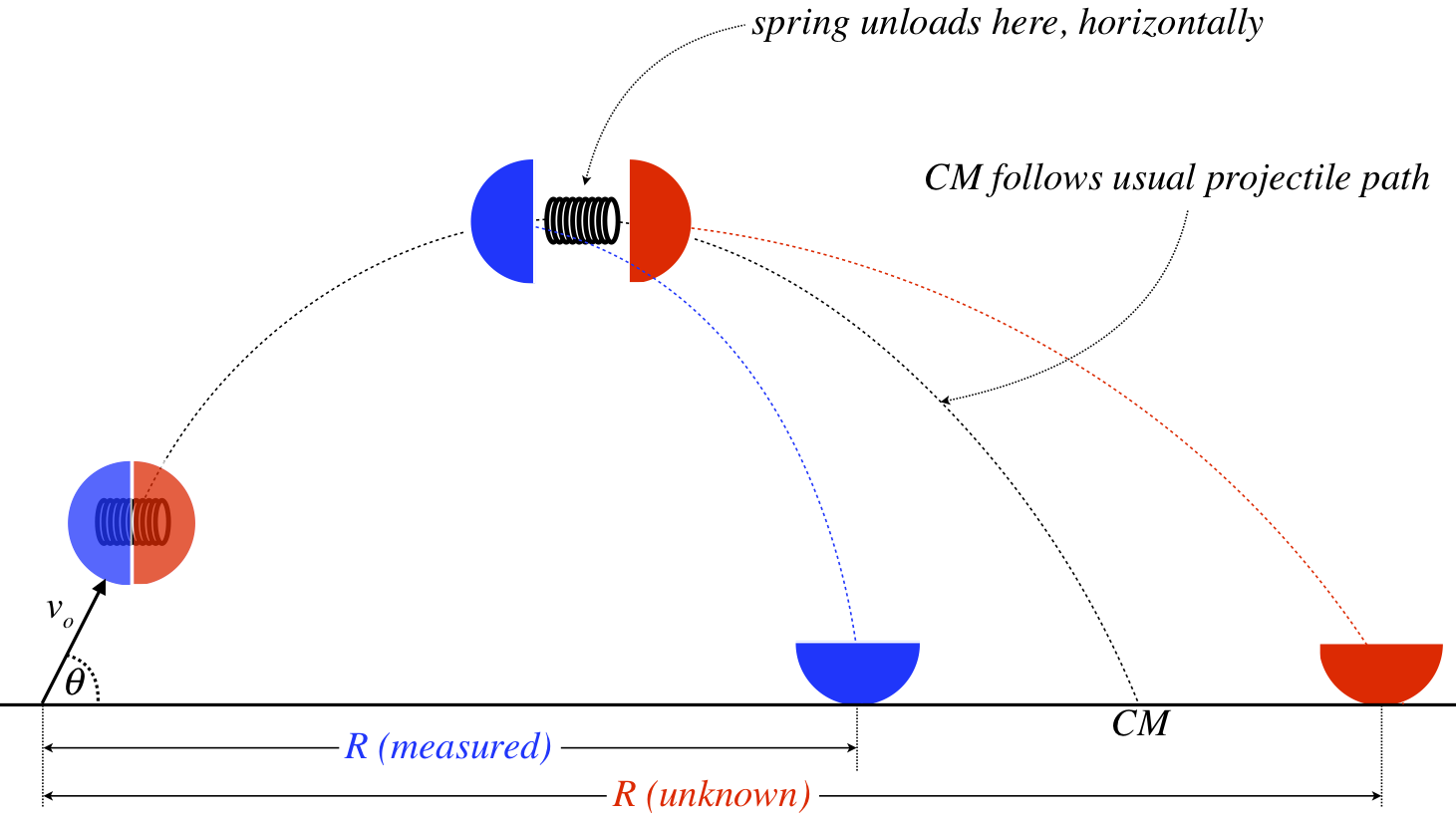
The forces on the shells by the spring are internal to the two-shell system, so assuming air resistance is negligible, the center of mass of the system will behave exactly as it would if the internal forces didn't exist. With the starting angle and speed known, the child can use the range equation (see Example 1.7.4) to calculate the landing point of the center of mass of the system. Then with the actual landing point of one piece of the toy, she can use the center of mass formula to compute the landing point of the other piece.

You might think we can do the same even if the spring unloads in an orientation that is other than horizontal, but this is not the case. The center of mass motion still follows the same parabolic trajectory, but naturally the center of mass is always between the two shells. In the case above, the shells land simultaneously (they both start with zero vertical component of velocity when the explosion occurs), so the center of mass lands at the same time, between the shells. When the explosion is not horizontal, one shell lands before the other, then friction stops is horizontal motion while the other shell keeps moving horizontally. This makes calculating the landing point of the center of mass using the usual range equation impossible.

Analyze This

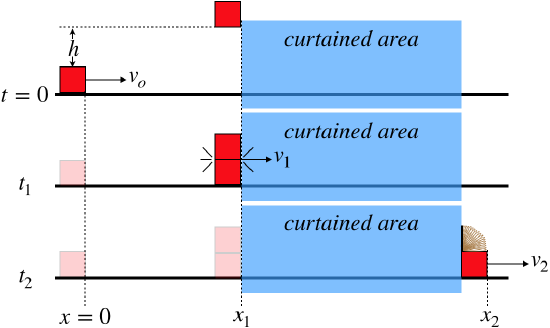
A block slides along a frictionless horizontal surface at a speed \(v\), starting at position \(x = 0\) and time \(t = 0\). An identical block dropped from rest lands directly on top of it. The surfaces of the blocks are sticky, so the top block adheres to the bottom block when it lands on it, and they continue along together. The blocks slide together into a curtained-off area, during which a spring noise and a “thud” are heard. At a later time, the bottom block emerges from the curtain without the top block on it, after apparently having its top lid sprung open from within.

Analysis

The collision of the falling block and the sliding block is an example of a case where the momentum of the a system is only conserved for one component. The blocks experience internal forces (normal force and static friction), and these have no effect on the two-block system momentum, but the horizontal surface pushing up on the bottom block is external, so although the two-block system had downward momentum just before the landing, the external force provides an impulse to take it away. However, the surface is frictionless, so there is no external force along the \(x\)-direction, and momentum is conserved along that direction. We can apply momentum conservation along that direction to write their combined speed \(v_1\) in terms of the bottom block's initial speed \(v_o\):

\[ mv_o + m\left(0\right) = 2mv_1 \;\;\; \Rightarrow \;\;\; v_1= \frac{1}{2} v_o\nonumber \]

We don't know the details of what happens behind the curtain – we don't know when the lid of the lower box sprung open, or where ((x\) position) it happened. But assuming that there are no external forces occurring behind the curtain, we can assume that the velocity of the center of mass of the two-block system along the \(x\)-direction is unchanged – the internal force from the spring-loaded box does not affect the center of mass motion.

We actually know the speed of the center of mass of the system behind the curtain, since both blocks are moving at the same speed as they enter. It is \(v_1\), computed in terms of \(v_o\) above:

\[v_{cm}=\frac{1}{2} v_o\nonumber\]

If we happen to know the speed \(v_2\) at which the bottom block emerges from the curtain, then we can use the known center of mass speed and speed of the bottom block to derive information about the other block.

\[v_{cm}=\frac{mv_{top}+mv_2}{2m}\;\;\;\Rightarrow\;\;\;v_{top}=2v_{cm}-v_2=v_o-v_2\nonumber\]

If we are given more information like the times \(t_1\) and \(t_2\) and the positions \(x_1\) and \(x_2\), we can derive more than just relationships between speeds.  For example, with the whole system located at \(x_1\) at \(t_1\), and knowing its center of mass speed, we know where the center of mass is at the later time \(t_2\). And combining this knowledge with the position of the bottom block (\(x_2\)) allows us to locate the position of the top block, even though it is hidden behind the curtain.

Rocketry

While we are on the topic of two parts of a system going their separate ways by pushed off each other, this brings us to the topic of rocketry. A rocket that is stationary in space somehow is able to accelerate itself by firing its engines. How can the center of mass of the rocket system accelerate without any external forces acting on it? Well, it can't of course, but the rocket (or rather, its fuselage) is not an isolated system. It expels fuel (in the form of very hot gas) backward. If we include the fuel as part of the system, then the center of mass of the system doesn't accelerate at all! All that matters in the end is that the fuselage of the rocket is propelled forward. Note also that the rocket has more mass than the fuel, but the ignited fuel sends particles away at very high speeds, and this momentum balances the momentum of the fuselage in the opposite direction (which has more mass and lower velocity).