4.4: Momentum and Energy
- Page ID
- 63000
Collisions
For the remainder of this chapter we will focus on what is the most common application of momentum conservation – collisions. A collision event can be a very complicated process, with lots of different objects taking part and interacting with each other with all sorts of different forces. Momentum conservation is very useful in these cases, because if every object involved is included in the system, the total incoming and outgoing momenta are equal, since the complicated internal forces don't affect the system's total momentum. This allows us to focus only on "before" and "after" conditions, as we can ignore what goes on in the intervening time.
In studying collisions, we will naturally not start with wildly complex cases. As always, we will start as simply as possible – with a head-on collision between one moving "projectile" object and another stationary "target" object. Because the collision is head-on, the motions of the objects will remain along the same line as the original motion of the projectile object. Later, we will allow both objects to move as they enter the collision, and we will extend the geometry of the collisions to include motions in two dimensions.
If the collisions are between two individual particles, then when they collide there is no way to move any of the original energy in the form of kinetic energy of the particles into internal energy (an object must consist of more than one particle to have internal energy). This means that the sum of the kinetic energies of the particles before the collision must equal the sum of their kinetic energies after the collision. If the collision is between two objects (collections of particles), then there is no way to avoid introducing internal energy to these objects, but if the particles in these objects are held in their positions very rigidly, then very little internal energy is introduced into the objects, and to a very good approximation the same "\(\sum{KE}_{in}=\sum{KE}_{out}\)" property that applies to particles also applies to macroscopic objects. We call such collisions elastic. Collisions between objects where this is not the case we call inelastic.
System Rest Frame Energy
In Section 3.2, we discussed the concept of internal energy for a collection of particles. We defined this as the total energy (kinetic and potential) of a group of particles as measured in the reference frame of the collection. We eventually noted that this internal energy virtually always manifests itself as thermal energy – energy randomly and unpredictably distributed amongst a large number of particles. Now that we are talking about collections (which we now call "systems") of larger objects, we will find it useful to introduce a concept similar to internal energy for these systems. If we define a group of objects to be a closed system, then we can define this system's rest frame energy as the total energy of that system measured in the reference frame where the system's center of mass is at rest.
Clearly this definition is identical to that of internal energy for particles, but we give it a new name to distinguish it from the case where we don't ever actually look at the detailed motions and potential energies between the constituent particles. The reason for defining this quantity at all will become obvious in its usefulness shortly. The main thing we need to keep in mind is that this quantity can only change if forces act on the system from outside – interactions between objects in the system change the forms of energy within the system, but never the amount of rest frame energy. In this regard it has much in common with momentum, and we will next see how intertwined these two physical properties are.
"Perfectly" Inelastic Collisions
Let's solve a simple collision problem using conservation of momentum, and make an accounting of what happens to the energy as a result of this collision. This collision consists of two clay balls. Initially ball #1 is moving toward ball #2, which is stationary. The collision is direct, and the two lumps of clay deform and mash together into one mass of clay, moving-off together. Collisions of this kind where the two objects end up with the same velocity at the end are called perfectly (or totally) inelastic.
Figure 4.4.1 – Perfectly Inelastic Collision
If we know the two masses \(m_1\) and \(m_2\) and the incoming velocity \(v_1\), momentum conservation gives us the final velocity \(V\):
\[\underbrace{p_1+p_2}_{\text{before}}=p_\text{after}\;\;\;\Rightarrow\;\;\; m_1v_1+0=MV\;\;\;\Rightarrow\;\;\; V=\frac{m_1}{m_1+m_2}v_1\]
Comparing this to Equation 3.2.3 (with \(v_2=0\)), we see that \(V\) is just the center of mass velocity. This is actually not that surprising. With no external forces, the center of mass of this two-object system should not change speed, and since the two balls combined are moving at a single speed, that speed would have to be the center of mass velocity of the system before the collision, and this is exactly what we recognize it to be. Next let's look at what happens to the kinetic energy:
\[\Delta KE = {KE}_{after}-{KE}_{before} = \frac{1}{2}MV^2-\left(\frac{1}{2}m_1v_1^2+0\right)=\frac{1}{2}\left(m_1+m_2\right)\left(\frac{m_1}{m_1+m_2}v_1\right)^2-\frac{1}{2}m_1v_1^2=-\left(\frac{m_2}{m_1+m_2}\right)\frac{1}{2}m_1v_1^2\]
The negative sign indicates that kinetic energy is lost during the collision, and the last quantity in parentheses is the original kinetic energy, so the fractional amount of kinetic energy lost is:
\[\text{fraction of KE lost}=\frac{m_2}{m_1+m_2}\]
Where does this kinetic energy go? Well, the two-object system is isolated, so it cannot simply vanish - it can only change form. In particular, it has to go into the internal energy of the two clay balls. The particles that comprise the clay balls start vibrating faster in a random fashion, i.e. the thermal energy of the clay balls goes up.
Okay, now let's approach the same collision from the perspective of the rest frame energy of the system. The first thing we need is the velocities of the two clay balls before the collision as measured in the center of mass frame. We know the velocity of the center of mass already, so we just need to subtract this from the velocities of the two clay balls to get their velocities in the new frame:
\[\begin{array}{l} \text{starting velocity in cm frame of }m_1=v_1-v_{cm}=v_1-\left(\frac{m_1}{m_1+m_2}v_1\right)=\frac{m_2}{m_1+m_2}v_1\\ \text{starting velocity in cm frame of }m_2=0-v_{cm}=-\frac{m_1}{m_1+m_2}v_1\end{array}\]
The rest frame energy of this system is the sum of the kinetic energies derived from these velocities (ignoring for now the contribution of whatever thermal energy is in the clay balls prior to the collision):
This is exactly the amount of lost kinetic energy that we calculated above. We interpret this result as follows:
- The system in the "before" state possesses a certain amount of rest frame energy. In this case, this rest frame energy is the sum of the kinetic energies of the clay balls (measured in the center of mass frame) as well as their starting thermal energies.
- When objects within a closed system collide, the forces involved in the collision reshape the form this energy, but since the system is closed, the total energy remains the same. In this case, the two clay balls stick together and their amalgamation remains at rest (again, in the center of mass reference frame). There is no longer any kinetic energy present – it has all be reshaped into thermal energy, which is added to whatever thermal energy the clay balls started with.
- In the previous calculation, performed in the frame where clay ball #2 was stationary (often referred to as the laboratory frame), the system still has the same rest frame energy (this quantity, like internal energy for collections of particles, is intrinsic to the system), and since all of this is converted into thermal energy, we see the total kinetic energy in the laboratory frame drop by exactly this much.
In short, perfectly inelastic collisions simply have the effect of converting all of the rest frame energy from easily observable kinetic energy of macroscopic objects into random, microscopic kinetic and potential energies of particles (thermal energy). One can compute this kinetic energy "loss" by either computing the rest frame energy (by changing reference frames), or by using momentum conservation. It is a subtle thing, but these ultimately boil down to the same physical principle.
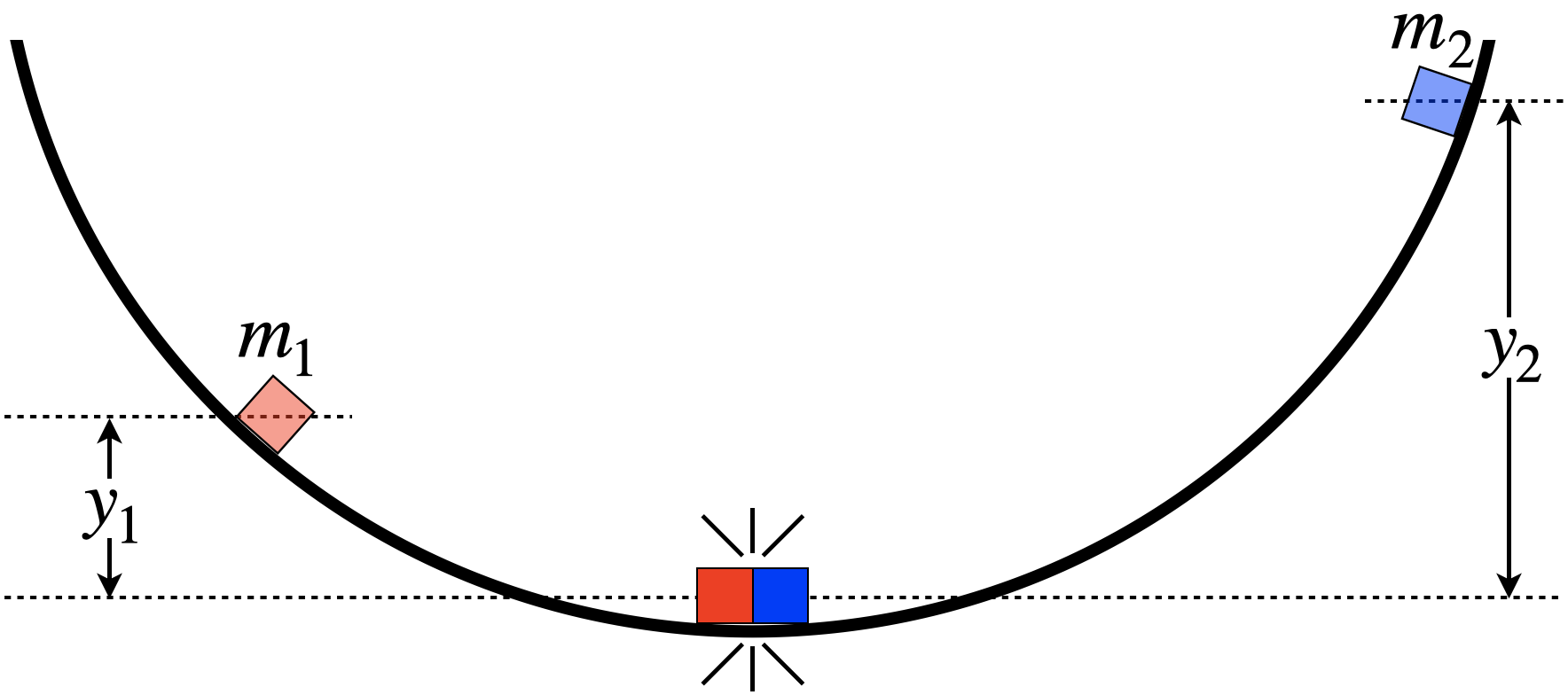
Two blocks slide down opposite sides of a frictionless curved ramp from different heights, colliding at the exact bottom, as shown in the diagram below. Upon colliding, they stick together, and move as a single entity thereafter (if they move at all).
- Analysis
-
Although we know the blocks collide at the bottom, we are not given any information about the timing here. They travel different distances to get to the bottom, so they may be released from rest at different times, or \(m_2\) may be given more initial downward speed than \(m_1\), or any number of other possibilities could account for the blocks meeting at the bottom. But we can nevertheless say a few things about what happens here.
The first thing we can say is that if we define the bottom of ramp as \(U_{grav}=0\), then all of the energy in the two-block system is kinetic. The total system energy is therefore:
\[E_{tot}={KE}_1+{KE}_2=\frac{p_1^2}{m_1}+\frac{p_2^2}{m_2}\nonumber\]
We also know that the momentum is conserved for the collision, so the momentum of the two-block combination (which is moving as one mass after the collision) is the sum of the momenta of the two blocks. Calling rightward the \(+x\)-direction, the value of \(p_2\) below is a negative number:
\[p_f=p_1+p_2\nonumber\]
If the momentum of the left block at the bottom is greater than the momentum of the right block, then \(p_1+p_2>0\) and the combination will continue to the right, and if the right block's momentum is greater, then \(p_1+p_2<0\) and it will continue to the left. We can determine how high on the ramp the two-block combination will go (in either direction) by using mechanical energy conservation. At the moment of the collision, all of the double-block's energy is kinetic, and when it stops on the ramp, it is all potential, so conservation demands:
\[{KE}_o=U_f\;\;\;\Rightarrow\;\;\;\frac{p_f^2}{2M}=Mgy_f\;\;\;\Rightarrow\;\;\;y_f=\frac{\left(p_1+p_2\right)^2}{2gM^2}\nonumber\]
We can speculate about some possible extensions to this problem. One that comes to mind is having the two blocks coming to a dead stop upon colliding. In this case, the final momentum is zero, which means that the blocks have equal magnitudes of momenta at the bottom: \(p_1=p_2\). If this is true, then it means that the ratio of the their collision kinetic energies (and therefore their total energies at earlier times is related to the ratios of their masses:
\[\frac{ {KE}_1}{ {KE}_2}=\dfrac{\frac{p_1^2}{2m_1}}{\frac{p_2^2}{2m_2}}=\frac{m_2}{m_1}\nonumber\]
So for the blocks to stop dead at the center, if \(m_1\) is \(n\) times as much mass as \(m_2\), then block #1 must enter the collision with \({\frac{1}{n}}^{th}\) as much kinetic energy as block #2. If they both happen to start from rest (at different times, so that they reach the bottom at the same time), then the kinetic energy comes is directly related to the heights from which they start (since they start with energy that is entirely potential), which gives us a ratio of the starting heights in terms of the mass ratio:
\[\frac{ {KE}_1}{ {KE}_2}=\frac{U_1}{U_2}=\frac{m_1gy_1}{m_2gy_2}=\frac{m_2}{m_1}\;\;\;\Rightarrow\;\;\;\frac{y_1}{y_2}=\left(\frac{m_2}{m_1}\right)^2\nonumber\]
We can of course speculate about different scenarios as well, such as knowing the starting heights and calculating the final height if the blocks do not stop dead, or perhaps giving the blocks some initial speeds.
Other Inelastic Collisions
As we noted above, all collisions involving objects (as opposed to particles) are to some degree inelastic, as the particles in the object can never be held perfectly rigidly in place. Let's have a look at inelastic collisions where the objects don't stick together and have the same speed at the end. In these cases only some of the system rest energy is converted from kinetic energy into thermal energy. Some of it remains in the form of kinetic energy of the objects. This is best demonstrated with a simple example. Consider a collision between two unequal masses where a projectile object hits a target (stationary) object head-on, and the result is that the projectile stops entirely, while the target moves off.
Figure 4.4.2 – Another Inelastic Collision
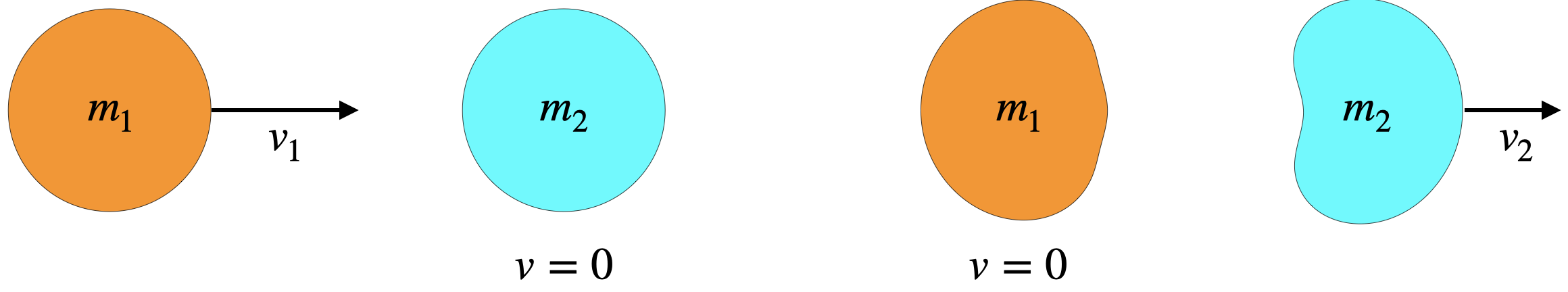
Let's start by solving for the kinetic energy converted to thermal energy in this collision using momentum conservation. Setting the before and after momenta equal, we get:
The change in the system's kinetic energy is therefore:
\[\Delta KE={KE}_f-{KE}_o=\frac{1}{2}m_2v_2^2-\frac{1}{2}m_1v_1^2=\frac{1}{2}m_2\left(\frac{m_1}{m_2}v_1\right)^2-\frac{1}{2}m_1v_1^2=\left(\frac{m_1}{m_2}-1\right)\left(\frac{1}{2}m_1v_1^2\right)=\left(\frac{m_1}{m_2}-1\right){KE}_o\]
This result tells us a couple of things. First, if the two masses happen to be equal (\(m_1=m_2\)), then when the incoming object stops and the other continues, all of the energy remains kinetic, as the change equals zero (the collision is elastic). Of course, with the diagram showing deformation of the two objects requires that internal energy is given to the two objects (the particles in the objects are pushed closer together, making them interact differently with each other).
Second, this kind of collision can only have a loss of kinetic energy if \(m_1<m_2\), so that the change is negative. If there is a spring compressed on object #2, waiting to be triggered by the collision, then it is possible for the energy stored in that spring to go into the kinetic energies of the two objects, making the change in kinetic energy positive. In this case, to have the projectile stop and the target move away, we would need \(m_1>m_2\). Most collisions we encounter in the real world do not involve stored potential energy waiting to be released, so we will continue to focus on the one described above.
Okay, so how does this fit with the system rest energy description? Well, we first note that in this case the kinetic energy in the rest frame of the center of mass is non-zero both before and after the collision. So unlike the perfectly inelastic case, not all of this rest frame kinetic energy is converted to thermal. With a bit of math, we can confirm that once again the kinetic energy lost from the system rest energy is the amount converted to thermal. Noting that the starting rest frame kinetic energy before the collision is the same as before, given by Equation 4.4.5 above. Next, we can avoid some math by noting that after the collision, the situation is the similar to before, with \(m_1\) swapped with \(m_2\) and \(v_2\) in place of \(v_1\), so the rest frame kinetic energy can be just written-down by making these swaps. The change in the rest frame kinetic energy is therefore:
\[\left.\begin{array}{l} \text{system rest frame KE before} = \left(\frac{m_2}{m_1+m_2}\right)\frac{1}{2}m_1v_1^2 \\ \text{system rest frame KE after} = \left(\frac{m_1}{m_2+m_1}\right)\frac{1}{2}m_2v_2^2\end{array}\right\}\;\;\;\Delta {KE}_{\text{system rest frame}}=\frac{1}{2}\left(\frac{m_1m_2}{m_1+m_2}\right)\left(v_2^2-v_1^2\right)\]
Plugging-in Equation 4.4.6 gives:
\[\Delta {KE}_{\text{system rest frame}}=\frac{1}{2}\left(\frac{m_1m_2}{m_1+m_2}\right)\left[\left(\frac{m_1}{m_2}v_1\right)^2-v_1^2\right]=\left(\frac{m_1}{m_2}-1\right)\left(\frac{1}{2}m_1v_1^2\right)\]
So we see that the amount of kinetic energy that is lost in the lab frame all comes from the kinetic energy in the rest frame. This makes perfect sense, given that the collision doesn't change the center of mass velocity, which means the system's center of mass kinetic energy \(\frac{1}{2}m_{tot}v_{cm}^2\) doesn't change.
In summary, we find that in any collision of two objects, the energy converted from kinetic to thermal comes from the system's rest frame kinetic energy, and the fraction of that energy converted depends upon the details of the collision itself. It can range from zero (when the two objects are very rigid, so the collision is elastic) to all of the rest frame kinetic energy (when the two objects merge, and the collision is perfectly inelastic), but the amount converted can never exceed the rest frame kinetic energy.
The diagram below depicts a moment just before a collision of two balls made of bouncetech™, a material made by an engineering firm that develops new materials. This experiment was set up as a head-on collision in the center of mass reference frame of the balls. The company's goal is to lose as little kinetic energy as possible to thermal energy in the bounce. To their absolute horror, the two balls stick together! They determine the kinetic energy converted to thermal in this collision to be \(E_o\). They re-check their bouncetech™ formula, and realize that they left out an important ingredient, bounconium. When they repeated the experiment with the corrected mix, they got a much better result.
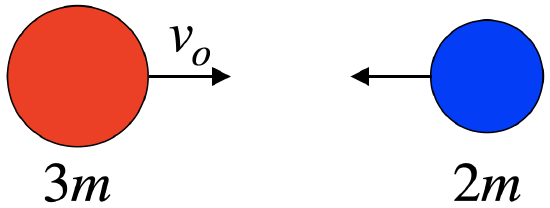
- Analysis
-
This experiment takes place in the center of mass frame, so there is a lot we can extract from what is given. First of all, when the balls stick together in the first experiment, they stop moving altogether, because by definition the center of mass cannot be moving in this frame, and the collision doesn't change this fact, so when they are stuck together, they cannot be moving.
The center of mass is not moving before the collision, so we can determine the speed of the blue ball:
\[v_{cm}=0=\frac{3mv_o-2mv_{blue}}{3m+2m}\;\;\;\Rightarrow\;\;\;v_{blue}=\frac{3}{2}v_o\nonumber\]
Given that they stop, all of the initial kinetic energy is converted to thermal, so in terms of these values, we can compute the thermal energy:
\[E_o=\frac{1}{2}\left(3m\right)v_o^2+\frac{1}{2}\left(2m\right)\left(\frac{3}{2}v_o\right)^2=\frac{15}{4}mv_o^2\nonumber\]
What if bouncetech™ achieved the impossible, and the collision cam out perfectly elastic? What would the motion look like after the collision? Well, first of all, in this center of mass frame, the balls would have to be going in opposite directions, or the center of mass could not remain stationary. Second, the ratios of the speeds of the two balls would have to remain the same as when they approached each other in order for the center of mass to remain stationary. And finally, the total kinetic energy has to add up to the same. Without even doing the math, there is a simple solution that satisfies all these criteria: The balls bounce back at the same speeds at which they came in.
The analysis of the elastic collision gives us an upper limit on the speeds at which we can expect to see the balls moving after the collision. Anything more is impossible, as the kinetic energy would have to increase. But anything less (all the way down to zero) is possible.
The Ballistic Pendulum
When it comes to perfectly inelastic collisions, there is one problem that stands out as a classic – the ballistic pendulum. The idea is to measure the muzzle velocity of a gun, and it goes like this:
A bullet is fired into a block of wood that is hanging by a string from the ceiling. The mass of the bullet and the block are given, as is the height to which the block rises. Find the incoming velocity of the bullet.
Figure 4.4.3 – The Ballistic Pendulum
If we break down the motion of the bullet and the block during the short span of time that the bullet is working its way into the block, things get very complicated, because the block begins to swing before the bullet comes to rest inside it, which means that the center of mass of the system is not quite moving in a circle yet. This is a problem because we will assume that the tension force does no work here, and we can only assume that if it acts perpendicular to the block+bullet system's motion, which must therefore be in a circle. Thankfully, the bullet is moving very fast, and gets imbedded into the block in a very short time, leaving very little time for the non-conservative part of the tension force to do damage to our results. We therefore neglect the time that the bullet takes to get into the block, and treat the block/bullet interaction as instantaneous.
Clearly this is an inelastic collision, and we can do this calculation in two parts. The first part consists of the momentum conservation problem that derives the speed of the block+bullet system immediately after the collision in terms of the incoming speed of the bullet and the two masses. Then the second part involves the mechanical energy conservation of the bullet+block swinging up to a new height and coming to rest.
Figure 4.4.4 – The Usual Breakdown of the Ballistic Pendulum
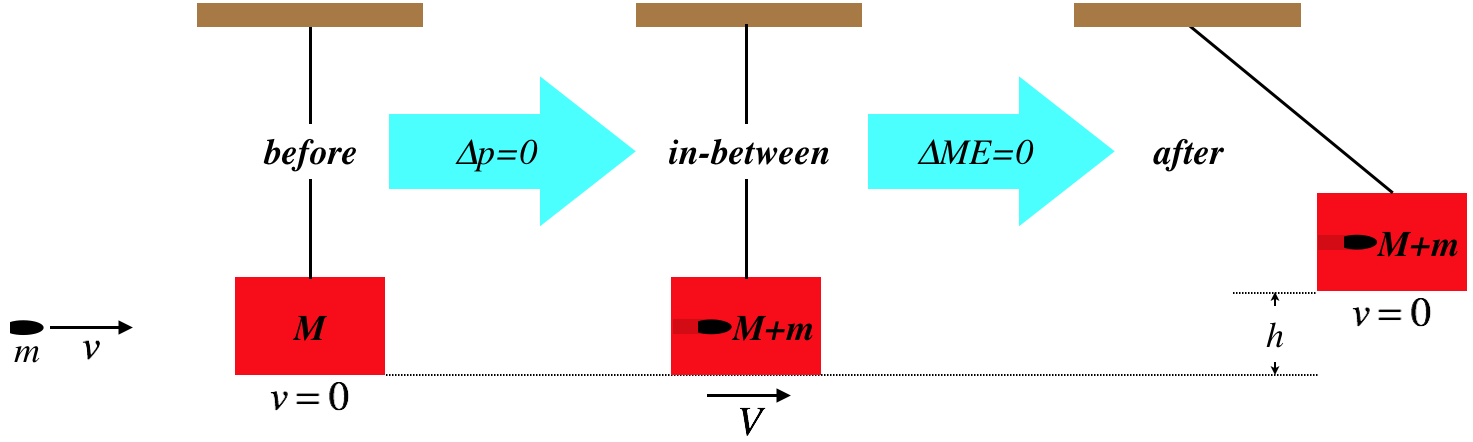
This is the way you will see this problem solved in virtually every textbook that covers this problem. But there is another way, which doesn't require these steps. The block+bullet system starts with some rest frame kinetic energy, and because their collision is perfectly inelastic, all of this energy goes into thermal. This leaves behind the energy of the system's center of mass, and since we are assuming that the tension does negligible work on the system, all of this goes from kinetic into potential. So:
\[U_f={KE}_o\;\;\;\Rightarrow\;\;\;\left(M+m\right)gh=\frac{1}{2}\left(M+m\right)v_{cm}^2=\frac{1}{2}\left(M+m\right)\left(\frac{mv+0}{M+m}\right)^2=\left(\frac{m^2}{M+m}\right)v^2\]
Solving for \(v\) gives:
\[v=\left(\frac{M+m}{m}\right)\sqrt{2gh}\]
There is nothing magical about this approach. It simply avoids re-solving the perfectly inelastic collision case, by noting that all the rest frame kinetic energy becomes thermal, and jumping straight to the center of mass kinetic energy. Both of these methods involve the same physical principals of momentum and energy conservation.
A large sled is at rest on a horizontal, frictionless sheet of ice, when a heavy rock is thrown onto it from behind. The rock is moving purely horizontally when it comes into contact with the sled, and it skids across the rough top surface of the sled until it and the sled are moving forward together at the same speed.
- Analysis
-
While we have significantly more detail about the force interaction of the two colliding objects, this collision is still perfectly inelastic, with a stationary target, just like the two clay balls discussed at the start of this section. We can therefore use the same conclusion about the fraction of initial KE converted into thermal energy that we found then:
\[\frac{E_{thermal}}{E_o} = \frac{m_2}{m_1+m_2} = \frac{m_{sled}}{m_{rock}+m_{sled}}\nonumber\]
Suppose we are given the mass of the rock and the coefficient of kinetic friction between the rock and the sled. We then know the amount of the kinetic friction force between the two colliding objects. From here, we can be given one of two pieces of information about the rock's trip across the surface of the sled. If we know how long it takes the rock to stop sliding, then from the constant friction force and the time, we know the impulse the rock delivers to the sled, and from that the new momentum of the sled, and if we know the mass of the sled, then we also know its speed at the end.
\[J_{\text{on sled}}=\Delta p\;\;\;\Rightarrow\;\;\;\left(\mu_k m_{rock}g\right)\Delta t=m_{sled}\Delta v=m_{sled}v_f\nonumber\]
The final speed of the rock is the same as the final speed of the sled, and the rock experiences the same impulse as the sled (except that it is negative), so we can compute the incoming speed of the rock:
\[J_{\text{on rock}}=-J_{\text{on sled}}\;\;\;\Rightarrow\;\;\; -\left(\mu_k m_{rock}g\right)\Delta t=m_{rock}\left(v_f-v_o\right)\nonumber\]
The other thing we can be given regarding the rock's trip across the sled is the distance it skids, \(\Delta x\). In this case, we can use what we previously found when we examined the case shown in Figure 3.5.2: The work done by kinetic friction as the rock slides across the sled is the amount of energy converted to thermal. We know from the very first example above with a stationary target, the fraction of the total energy this is:
\[\text{work done by friction}= f\Delta x =\mu_km_{rock}g\Delta x= E_{thermal} = \frac{m_2}{m_1+m_2}E_{total}=\left(\frac{m_{sled}}{m_{rock}+m_{sled}}\right)\left(\frac{1}{2}m_{rock}v_o^2\right)\nonumber\]