11.7: Magnetic Field
- Page ID
- 80101
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Field of a Magnetic Dipole
Everyone has at least a passing experience with magnets – little metal disks we stick to refrigerators to hold papers we need to remember. From our experience, we know that if we put two magnets together a certain way, they stick together, and if we turn one of them around, they repel. So they clearly have a directionality to them. The convention is that these two distinct ends of a magnet are called the north pole and the south pole. This convention is related to the use of magnets in navigation. The development of the navigational compass (around the 12th century) makes use of the interaction between bar magnets and the Earth (which, for the purposes of magnetism, is one large bar magnet). The poles are defined thus: if we suspend any magnet freely on a table (by a string or sticking it to a cork which is free to float on a liquid, to name some examples) the end of the magnet that points towards the north geographic pole of the Earth is referred to as the “north-seeking pole” or just the north pole. The opposite end is the “south-seeking pole” or just the south pole.
Since there are two opposite poles on a magnet, the closest analogy in electricity is a dipole which has two opposite charges. Indeed, if we put two dipoles end-to-end one way, they will attract, and if we turn one of them around, they will repel.
Figure 11.7.1: Attraction of Aligned Electric Dipoles
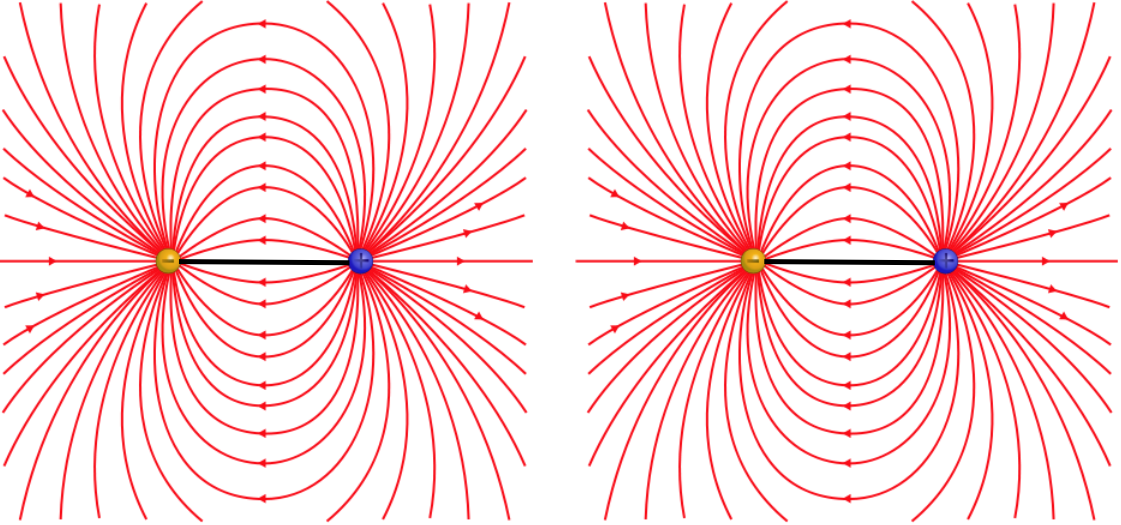
Figure 11.7.2: Repulsion of Anti-Aligned Electric Dipoles
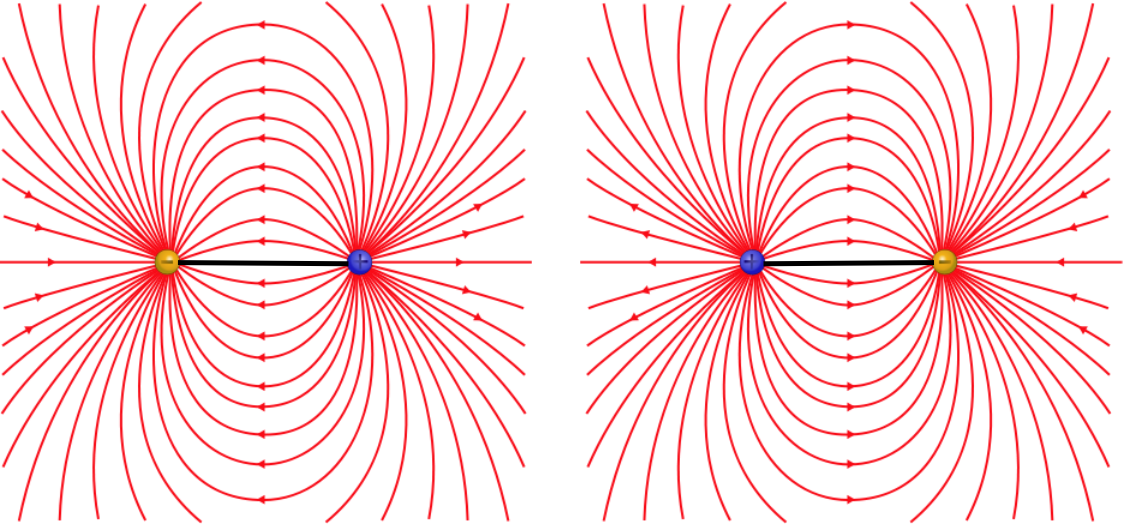
The attraction and repulsion occur because the there is a field created by one dipole that points in the direction outward from the positive charge, and the field gets weaker with distance, so the other dipole will feel a net force according to whichever of the two charges is closer to the dipole creating the field. In magnetism, we call the end of the magnet from which the outward-going field lines emerge, the north pole, and the end into which the field lines converge, the south pole. From the figures above, it's clear that the dipoles whenever like poles are brought together, and attract when opposite poles are brought together.
Okay, so this looks like a reasonable explanation for how magnets work, so if we want to isolate the two individual magnetic charges (a "north charge" and a "south charge"), all we have to do is cut the magnet in half, right?
Figure 11.7.3: Isolating Magnetic Charges from a Magnet – An Attempt
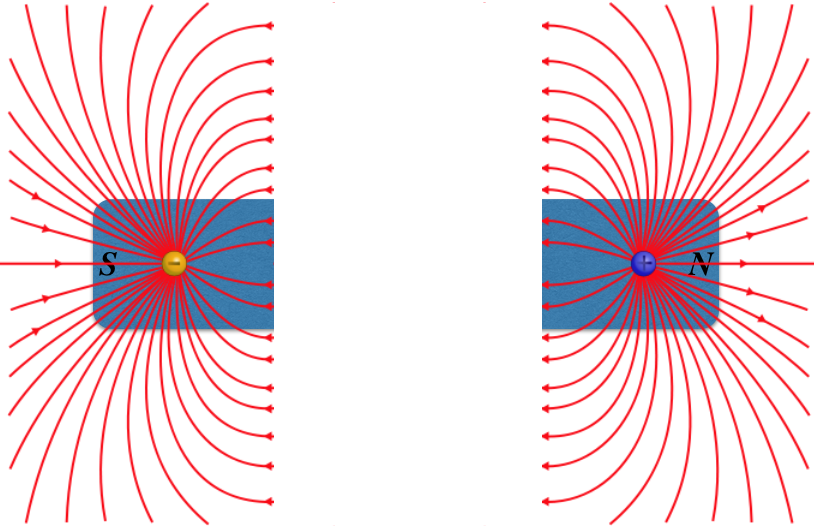
Well, try as we might, this never happens. Instead, every time we cut a magnet with two poles into two pieces, we just get two more magnets with two poles!
Figure 11.7.4: Isolating Magnetic Charges from a Magnet – What Actually Happens
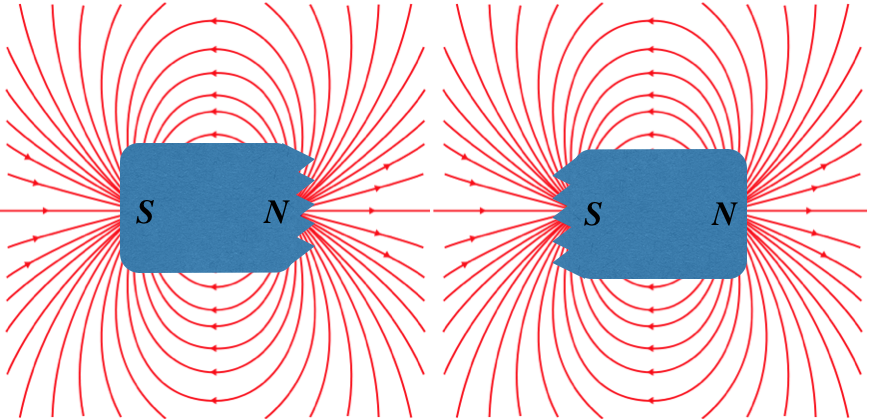
If we examine the the field lines for a bar magnet closely and compare them to an electric dipole field, we see how fundamentally-different the two fields are. For the electric dipole, the field changes direction between the two poles, while for the magnetic case, the field lines continue straight through:
Figure 11.7.5: Comparing Field Lines of Electric and Magnetic Dipoles
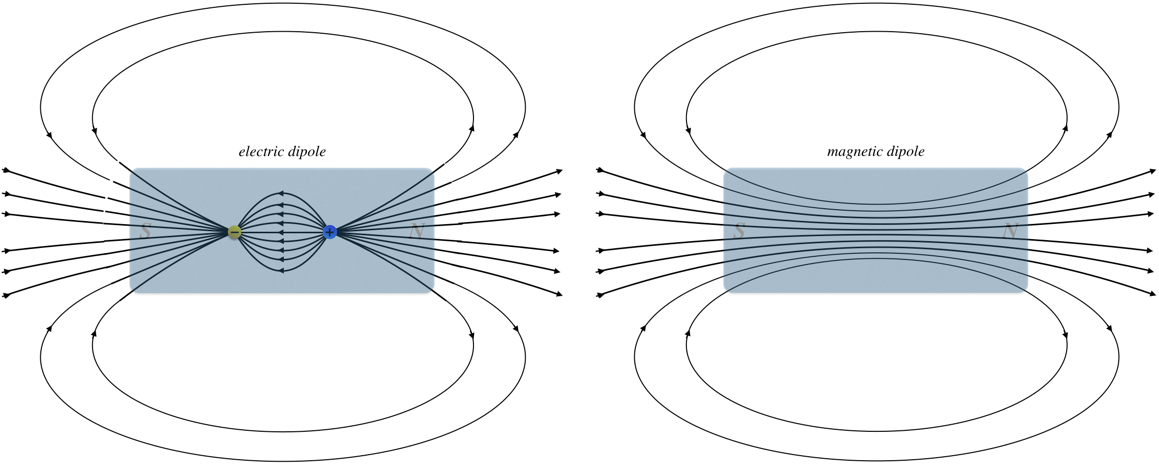
Outside the dipoles, the fields look the same, but they are clearly different, which we can characterize in the following way:
Magnetic field lines always form closed loops, while electric field lines begin and end on electric charges.
Put another way, unlike electric fields which form their dipole fields from two monopoles, there don't seem to be any magnetic monopoles. Or at least we have never been able to detect a magnetic monopole, despite many decades of experimental search for them. It turns out that electromagnetic theory doesn't exclude the possibility of the existence of these point charges of magnetism, but ultimately our theories have to agree with what we observe in experiments, so at least for the moment (and for the duration of this class), we will maintain the position that they simply don't exist.
Magnetic Dipole
For the electric field we described the force that a electric charge feels in an external field. Then, we also explored the force that an electric dipole feels in the presence of an external field in Section 11.5. Let us compare the electric dipole interaction with one for a magnetic dipole, since there is no magnetic monopole to make the comparison with a point charge. All magnets are magnetic dipoles, so we want to explore what happens when you place a magnet in an external magnetic field which, for example, is generated by another bar magnet. The "test" dipole magnet can be a magnetic needle of a compass.
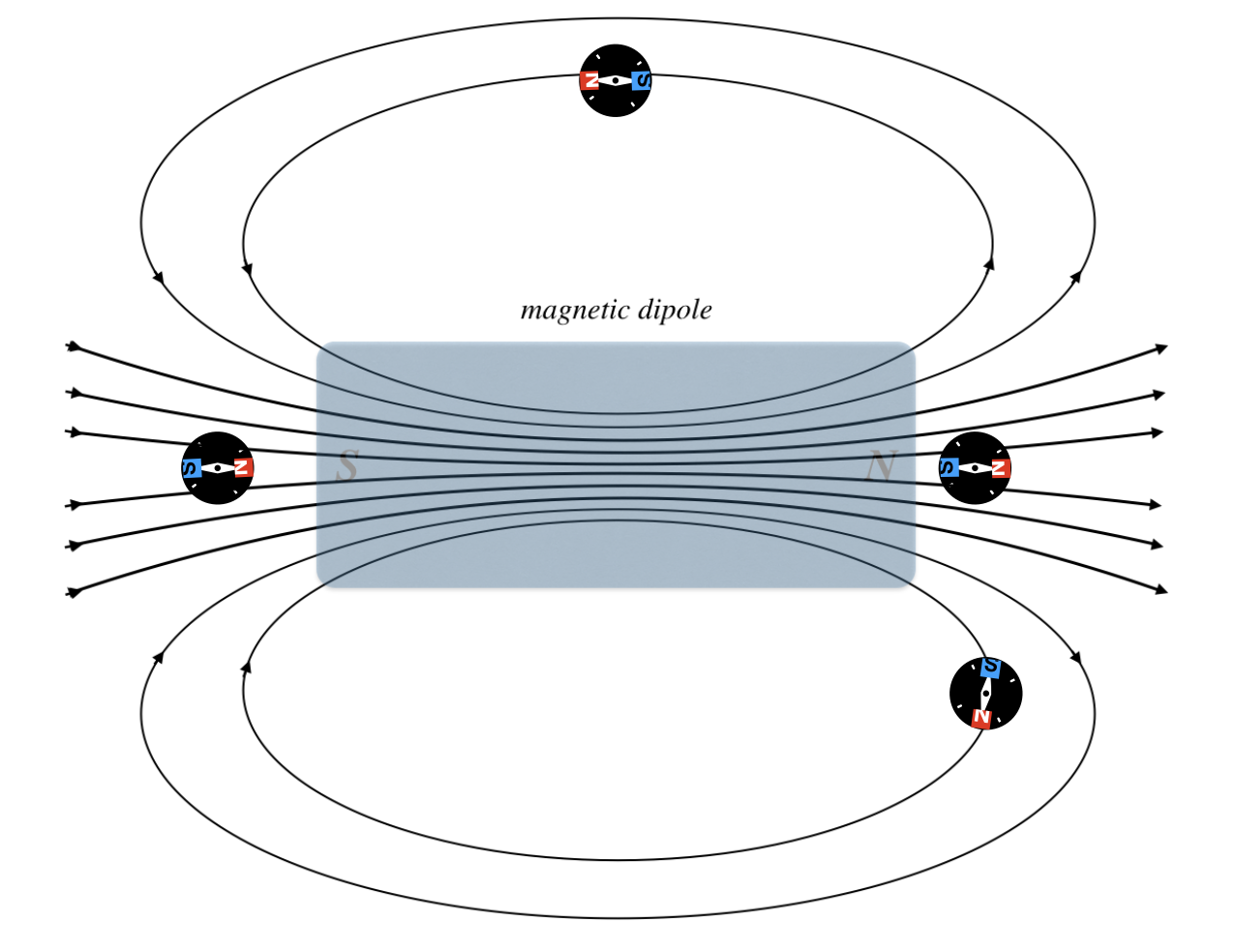
The bar magnet produces a magnetic field in its surrounding space, and the magnetic needles of the compass reorient themselves because the field exerts a force on them. For example, the compass needle that is exactly to the right of a bar magnet is closest to the North pole of the bar magnet. Therefore the north pole of the compass needle will be repelled by the north pole of the bar magnet, so it will now point to the right as shown in the diagram below. The opposite happens at the south end of the magnet. Placing the compass at different locations around the magnet, we discover that the magnetic needle always lines up with the external magnetic field, such that the north end of the needle points in the direction of \(\vec B\).
Figure 11.7.6: Magnetic Dipole in an External Magnetic Field
For electric dipoles we defined the electric dipole moment, \(\vec p\), and showed that it lines up with the external electric field, \(\vec E\). The potential energy of this interaction was described by the equation shown in the figure below. Likewise, let us define the magnetic dipole moment, \(\vec\mu\), which points from the south end to the north end of a magnet. Thus, magnetic dipole moment, \(\vec\mu\), will line up with the external magnetic field, \(\vec B\). The equation that describes the magnetic potential energy of this interaction is shown below.
Figure 11.7.7: Comparing Electric and Magnetic Dipole Interactions
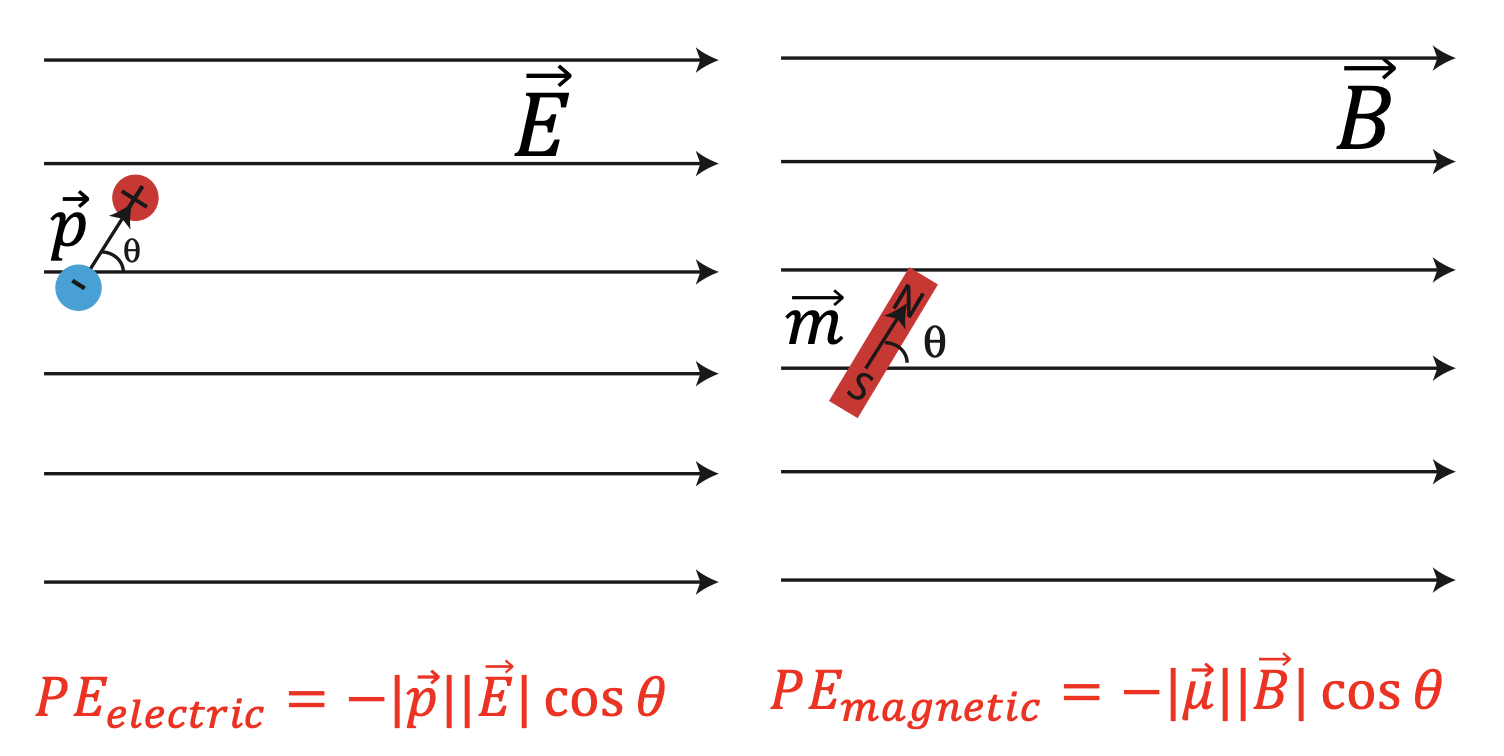
Although, the two dipoles describe physically different situations, the analog between the two interactions is strikingly similar.


