9.1: Background Material
( \newcommand{\kernel}{\mathrm{null}\,}\)
Text References
Our Heat Engine
In this lab, we will be using a simple heat engine which consists of an airtight piston and two thermal reservoirs. The cold reservoir is an ice water bath at 273K, and the other is boiling water at ≈373K. We will extract work from this engine by placing a weight on the piston when the trapped air is cold, then heat the gas so that it expands and the piston raises the weight. After it is raised, the weight is removed, and the engine is returned to its initial state to complete the cycle.
We don't want to over-complicate the cycle we are looking at, so we would like it to consist of just four processes. The weight is placed atop and later removed from the piston very suddenly, so these two processes occur with very little time for any heat to be exchanged. The expansion and compression of the piston occur while the same weight is pressing down, so during these processes, the gas is held at a fixed pressure. Given the properties of these processes, we would expect a PV diagram to look roughly like this:
Figure 9.1.1 – Our Engine Cycle
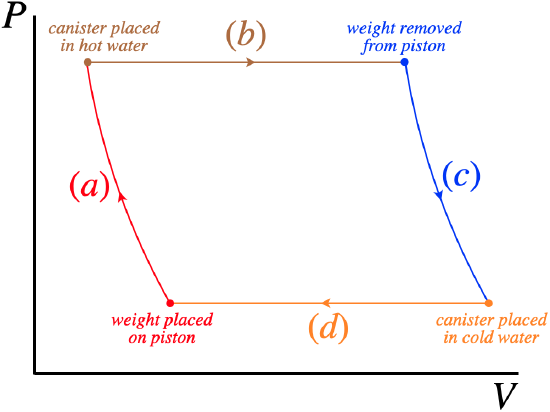
While the four actions we have to take are clear (moving the weight and changing the reservoir), actually achieving this process requires some careful timing. Consider, for example, what happens after placing the weight on the piston. Process (a) in the diagram occurs very quickly, and then it is time to start process (b). This means that the reservoir needs to be swapped essentially during the very brief time that the weight is placed. What is wrong with placing the weight first and delaying the swap of reservoir? Well, the sudden compression of the air by the placement of the weight increases its temperature, and if the canister is left in the cold water, the air will begin to give back heat to the water. This results in a constant-pressure compression at the end of process (a), before starting process (b) (which is a constant pressure expansion). This shows up as an ugly "notch" in our PV diagram in the upper-left corner. Similarly, to prevent unwanted intermediate energy exchanges between processes (c) and (d), it will be important to swap the thermal reservoir while removing the weight from the piston.
Dealing with Friction
In order to ensure that no gas escapes the engine, the piston needs to rub against the inner surface of the cylinder. This is obviously going to introduce friction into our process. The potential energy of the weight is changed by the total work performed on it, which is the combination of the positive work done by the engine and the negative work done by friction. So in order to confirm that work we compute from the PV diagram equals the work that goes out, we need to find both the change in potential energy of the weight and the work done by friction. We will be able to measure the mass of the lifted object and the height it is raised, but we need to be clever to determine the work done by friction.
We begin with a free-body diagram of the piston. The weight on it always acts downward, and the force by the gas is always upward, but the friction force direction depends upon whether the gas is expanding (piston moving up) or compressing (piston moving down).
Figure 9.1.2 – Forces on the Piston
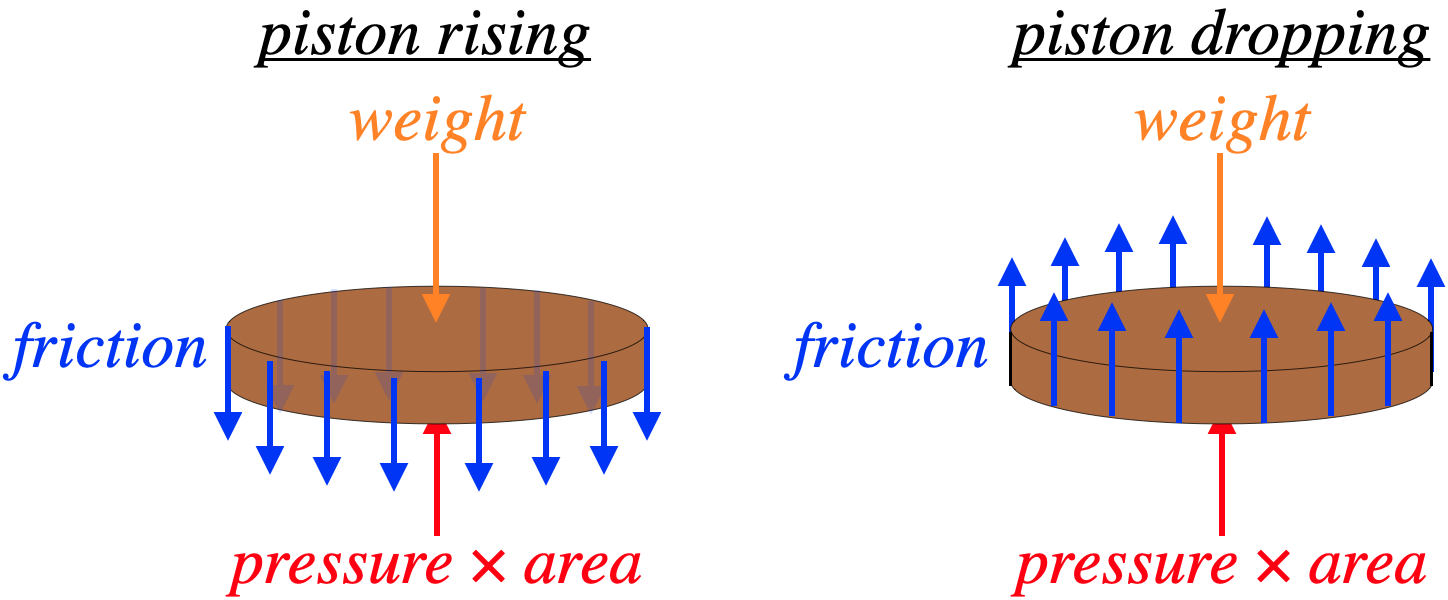
The piston moves at a pretty steady, slow rate, so its acceleration is negligible, which means the net force on the piston is zero. The friction depends upon the contact force and the coefficient of friction between the surfaces, so it is the same whether the piston is rising or falling. The weight also obviously remains the same for both directions of piston movement. So this means that the force by the gas when the piston is rising is greater than the force when it is falling. If we measure the pressure in both cases, we can use the two numbers to compute the friction force:
(P↑A)−f−W=0(P↓A)+f−W=0}⇒f=P↑−P↓2⋅A
So all we need to do is run our engine in a cycle without ever removing the weight. The output should look something like this:
Figure 9.1.3 – The "Friction Run"
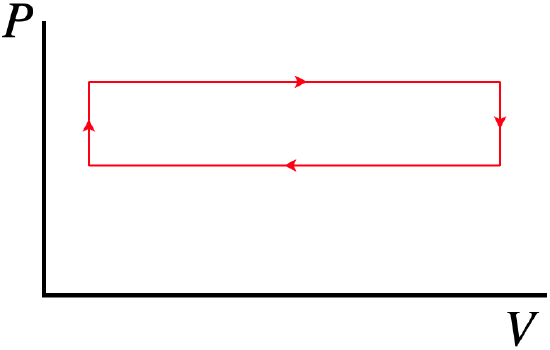
The vertical segments occur because the piston doesn't immediately move when the gas starts warming or cooling. This is because when the piston stops, static friction takes over for the rubbing friction, and the static friction needs to adjust to the changing external force before the piston can start sliding again. In any case, reading off the pressures for the top and bottom segments of this cycle gives us the friction force. With this and the distance that the piston travels, we can compute the work done by this force.
One might ask why we don't just find the area in this cycle to get the work done by friction for the cycle, rather than computing the friction force. The answer is that while we expect the friction force to be the same for every run, we cannot say that the piston will travel the same distance in the "friction run" as in the a-b-c-d cycle of our main experiment. Most notably, the friction run does not include the displacement of the piston that occurs during the quick compression/expansion that occurs when the weight is placed/lifted.
Engine Efficiency
The efficiency of this (and any) engine is the ratio of the net work that comes out and the heat that comes in from the hot reservoir (the heat that exits into the cold reservoir is not included). This engine is connected to the hot reservoir during legs (a) though (d). We know what types of processes these are, so with this information and the fact that air is a diatomic molecule, we can determine the heat transferred during each process in terms of changes of pressure and/or volume that we read off the PV diagram.
When you make this calculation in the lab that follows, you may be troubled by how low the efficiency comes out to be. To assuage your fears, you may want to consider that if this was the most efficient engine possible (a Carnot engine, which follows only isothermal and adiabatic curves), for the two temperatures we have available, the efficiency would be:
e=1−TCTH=1−273K373K=27%
Now when you take into account that we are assuming that the various processes are reversible (which they clearly are not, since the temperature difference between the gas and the reservoir is virtually always finite), we should expect the efficiency to be significantly lower than this number.


