3.1: Light as a Wave
( \newcommand{\kernel}{\mathrm{null}\,}\)
What is "Waving"?
The jump from mechanical waves to sound was a difficult one, mainly because the "displacement" of the wave changed from matter that oscillates back-and-forth, to (in the case of sound in a gas) oscillations in pressure or density. This difficulty gets greatly magnified for the case of light. We know that light is a wave based on how it behaves – it exhibits the same properties of other waves we have examined – it interferes with itself, it follows an inverse-square law for intensity (brightness), and so on. But we also know that we can see light from the sun, moon, and stars, which means that light waves can travel through the vacuum of space. Unlike every other wave we have seen, it doesn't require any medium at all! So what do we use as the "displacement" for our wave function?
Back in the 19th century, physicists studied extensively the subjects of electricity (lightning, shocking your finger on a doorknob, balloons sticking to your hair, etc.) and magnetism (compasses, sticking things to your refrigerator, etc.). It started becoming clear that the two forces, while different, had some links. Electric currents were found to affect compass needles, and magnets moving near wires were found to create electric currents. It all came together with an amazing (for the time) effort in mathematics by a man named James Clerk Maxwell. He showed that changing electric fields could induce magnetic fields, while changing magnetic fields could in turn induce electric fields. This is a recipe for propagation of these fields, and the equation he derived for this propagation was exactly the wave equation! So he predicted, from results taken from experiments in electricity and magnetism, that an electromagnetic wave could be produced. The wave equation included physical constants from both electricity and magnetism, and extracting the wave speed from this equation resulted in a number Maxwell was already familiar with – the speed of light. It is traditional to denote this speed with a lower-case 'c':
c=3.0×108ms
So the "displacement" of such a wave is actually the electric and magnetic field vectors (both types of fields are waving simultaneously, with each inducing the other) in the space through which the light wave is traveling. Don't worry that this doesn't make much sense right now – it should be a bit clearer when you get to Physics 9C and study electricity & magnetism.
Okay, so for light we now have the wave speed and the "displacement." Let's address a couple other elements of light as a wave. First, a medium is not needed, as electric and magnetic field can exist in a vacuum. The presence of a medium (such as air or water) does effect the electric and magnetic fields, because media are made up of atoms, which are composed of positive and negative electric charges. Because of this, the speed of light within a medium is different (slower) than its speed in a vacuum. Mathematics and experiments show that light is a transverse wave – the electric and magnetic field vectors point in directions that are perpendicular to the direction of motion of the light wave (and as it turns out, they also rare always perpendicular to each other).
Figure 3.1.1 – Electromagnetic Wave

The red arrows in the figure above represent electric field vectors, and blue arrows magnetic field vectors. Specifically, this is a plane-polarized EM wave, which means the field vectors of a given type remain in a single plane. We will discuss plane polarization soon, but it should be noted that EM waves do not have to behave this way, so long as the electric and magnetic field vectors remain perpendicular to each other and to the direction of motion. For example, a circularly polarized EM wave features electric and magnetic field vectors that circulate their directions (while remaining perpendicular to each other and the direction of motion) as the wave propagates, like the hands of an analog clock, and can do so in a clockwise or counterclockwise manner.
Finally, we need to say two things about light perception. For sound, intensity (proportional to amplitude-squared) is perceived as loudness, and for light it is brightness. For sound, frequency is perceived as pitch, and for visible light it is perceived as color. The qualification "visible" must be appended because we can only see a very limits spectrum of light frequencies, the rainbow of colors often described with the acronym ROYGBIV (Red, Orange, Yellow, Green, Blue, Indigo, Violet). The red end of the visible spectrum exhibit the lowest frequencies, and the violet the highest. But of course light waves can come in frequencies much lower and much higher, and at various arbitrary cutoffs, they are given names you have probably heard before. In order of increasing frequency below the red end of the visible spectrum we have: radio waves, microwaves, and infrared; and above the violet end of the spectrum: ultraviolet, x-rays, and gamma rays.
Huygens's Principle
When we discussed the case of a wave on a string, we said that the wave causes each particle on the string to vibrate up-and-down in harmonic motion. It should therefore not be surprising that if we grab the string at a single point and force it to vibrate in harmonic motion, that a wave will propagate away from that point. In fact, this gives us a way of describing how the wave propagates: The wave causes a single point to oscillate, which in turn causes a wave to be generated, which then vibrates another point, and so on. In the 17th century a Dutch scientist named Christian Huygens generalized this idea to three dimensions. The principle which now bears his name can be stated this way:
Every (3-dimensional) wave propagates by having every point on a wavefront being an independent generator of a new spherical wave, and the interference of all of those individual spherical waves results in the overall wave observed.
When we look at a single point light source, the farther away it is, the flatter the light wavefronts will be when they reach us. When the source is very far away (e.g. the sun), then the wavefronts are essentially flat. We call waves with such flat wavefronts plane waves, for obvious reasons. But now the question arises, “If Huygens’s principle is valid, how can plane waves occur?” After all, each point on the plane wave behaves as a point source of a spherical wave. Let's look at the spherical wave contributions of many point sources on a plane. We'll do this gradually, starting with just a few points on a plane, and filling in the spaces between them little-by-little:
Figure 3.1.2 – Plane Wave from Huygens's Principle
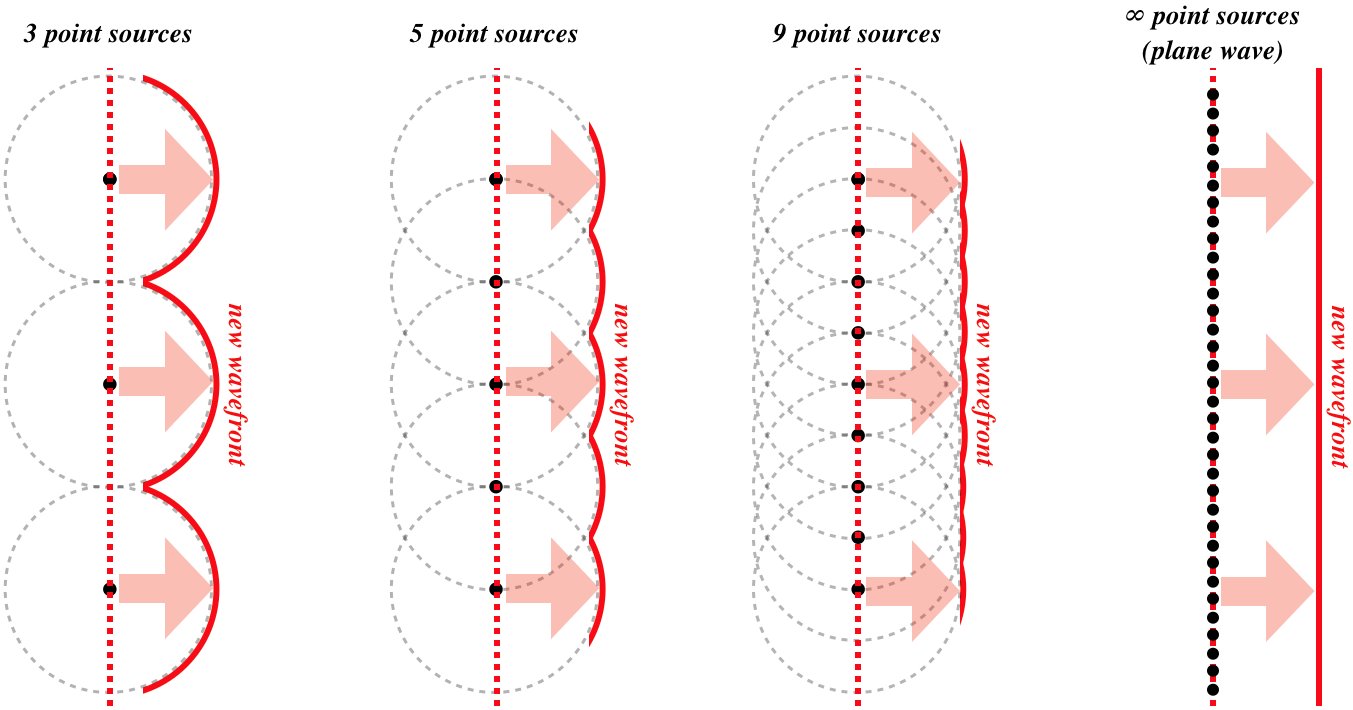
One might ask why a plane wave only propagates in a single direction. Suppose a plane wave propagating to the right. If each new wavefront becomes a source for a new wave, why don't waves come out of it in both directions? It is difficult to express in a simple diagram like the one above the effects of superposition, but the short answer is that there is destructive interference between all of the previous wavefronts and the new one, which results in zero wave energy traveling "backwards."
It should also be noted that a plane wave is a one-dimensional wave, which means that its intensity does not drop off with distance. But the intensities of the spherical wavelets do follow an inverse-square law. So if they get weaker with distance, why don't plane waves? The reason is that the farther a wavelet travels, the more other wavelets it encounters. These encounters result in constructive interference, bolstering the amplitude (and therefore the intensity) The rate at which the wavelets encounter other wavelets and constructively interfere is exactly enough to compensate for each wavelet losing its own individual intensity, maintaining the plane wave's intensity.
Where Huygens's principle becomes particularly useful is in explaining what happens when a plane wave encounters a barrier. A plane wave moves straight ahead because there is destructive interference of the wavelets in other directions. But a barrier removes a number of wavelets by either absorbing or reflecting the part of the wavefront from which those wavelets were going to spawn. The result is that the wave "bends around corners," a phenomenon known as diffraction.
Figure 3.1.3 – Diffraction from Huygens's Principle
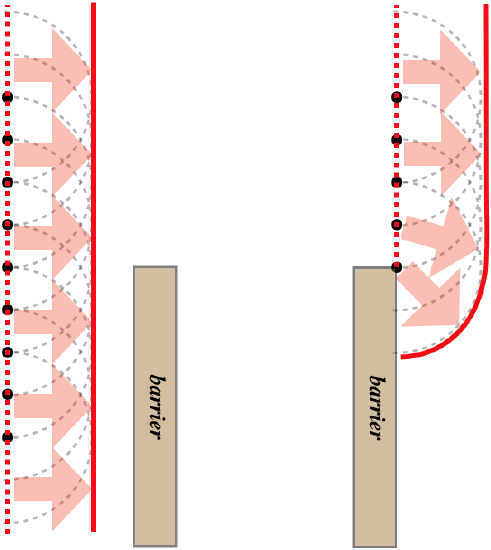
Like other wave phenomena, this is not unique to light. Ocean waves diffract around barriers like reefs, peninsulas, and docks. It's certainly possible to hear a sound made from around a corner. It should be noted that the part of a wave that diffracts around a corner is no longer a plane wave, and is subject to the reduction in intensity the farther it travels. Of course reflections of waves are also responsible for their ability to change direction in the presence of barriers, but the phenomenon of diffraction in conjunction with interference leads to other important observable properties that we will deal with next.
Alert
You should be aware that diffraction is so intimately tied up with the interference effects that it causes (the subjects of the next few sections) that many physicists use the word "diffraction" to indicate the interference phenomena themselves, rather than the "going around corners" definition.


