3.7: The Simple Dipole
( \newcommand{\kernel}{\mathrm{null}\,}\)
As you may expect from the title of this section, this will be the most difficult and complicated section of this chapter so far. Our aim will be to calculate the field and potential surrounding a simple dipole.
A simple dipole is a system consisting of two charges, +Q and −Q, separated by a distance 2L. The dipole moment of this system is just p=2QL. We’ll suppose that the dipole lies along the x-axis, with the negative charge at x=−L and the positive charge at x=+L. See Figure III.5.
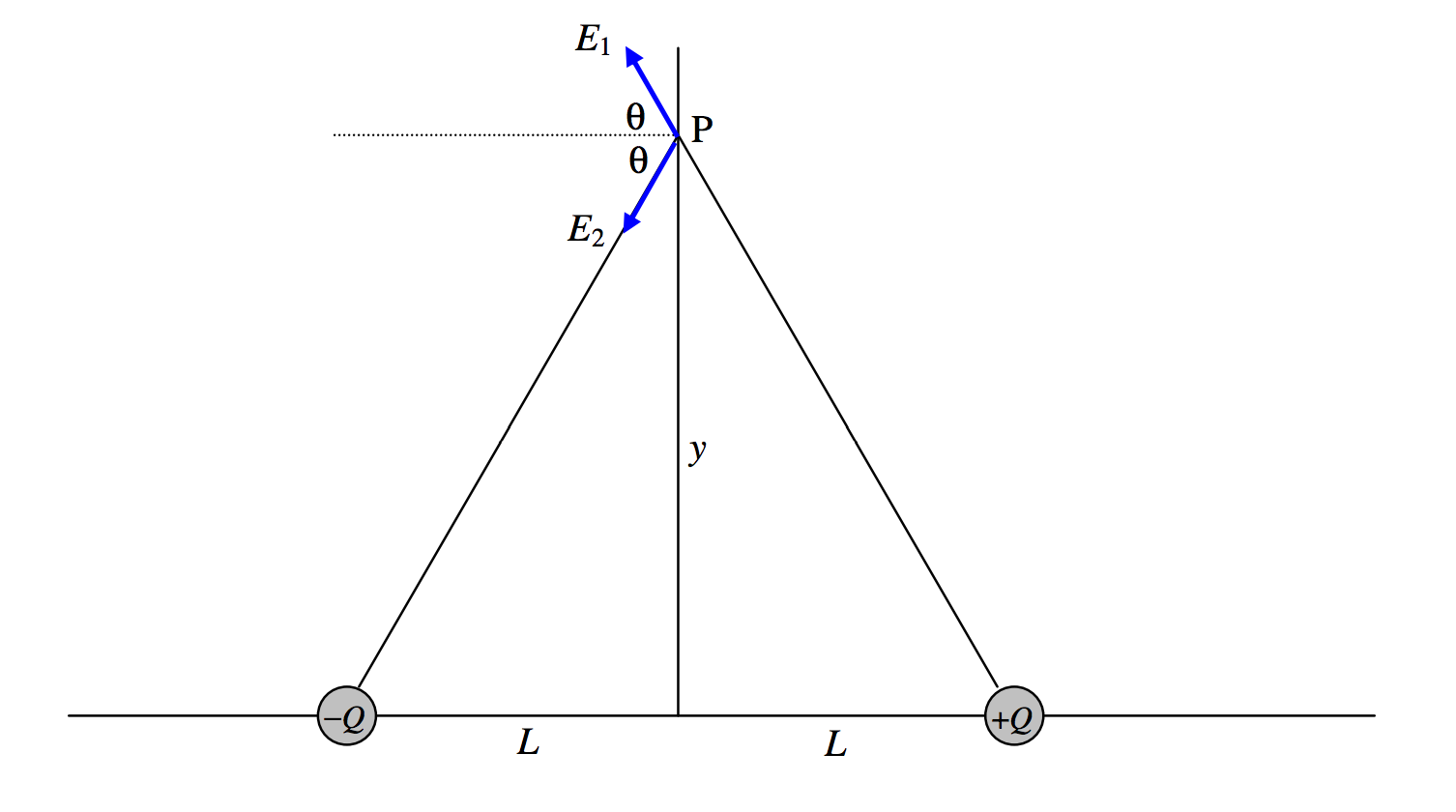
FIGURE III.5
Let us first calculate the electric field at a point P at a distance y along the y-axis. It will be agreed, I think, that it is directed towards the left and is equal to
E1cosθ+E2cosθ, where E1=E2=Q4πϵ0(L2+y2) and cosθ=L(L2+y2)1/2.
Therefore
E=2QL4πϵ0(L2+y2)3/2=p4πϵ0(L2+y2)3/2.
For large y this becomes
E=p4πϵ0y3.
That is, the field falls off as the cube of the distance.
To find the field on the x-axis, refer to Figure III.6.
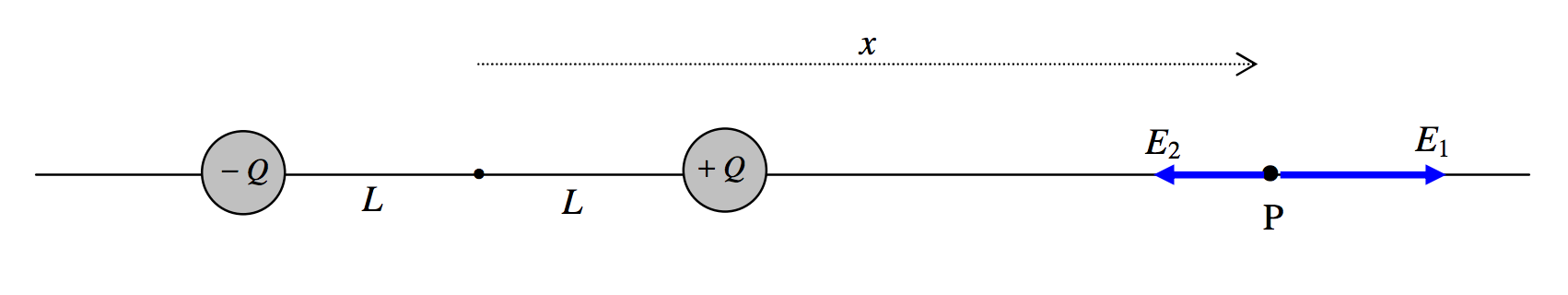
FIGURE III.6
It will be agreed, I think, that the field is directed towards the right and is equal to
E=E1−E2=Q4πϵ0(1(x−L)2−1(x+L)2).
This can be written Q4πϵ0x2(1(1−L/x)2−1(1+L/x)2), and on expansion of this by the binomial theorem, neglecting terms of order (L/x)2 and smaller, we see that at large x the field is
E=2p4πϵ0x3.
Now for the field at a point P that is neither on the axis (x-axis) nor the equator (y-axis) of the dipole. See Figure III.7.
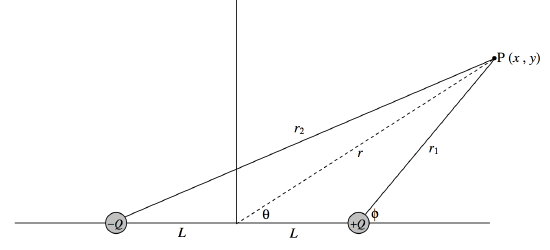
FIGURE III.7
It will probably be agreed that it would not be particularly difficult to write down expressions for the contributions to the field at P from each of the two charges in turn. The difficult part then begins; the two contributions to the field are in different and awkward directions, and adding them vectorially is going to be a bit of a headache.
It is much easier to calculate the potential at P, since the two contributions to the potential can be added as scalars. Then we can find the x- and y-components of the field by calculating ∂V/∂x and ∂V/∂y.
Thus
V=Q4πϵ0(1{(x−L)2+y2}1/2−1{(x+L)2+y2}1/2).
To start with I am going to investigate the potential and the field at a large distance from the dipole – though I shall return later to the near vicinity of it.
At large distances from a small dipole (see Figure III.8), we can write, r2=x2+y2,
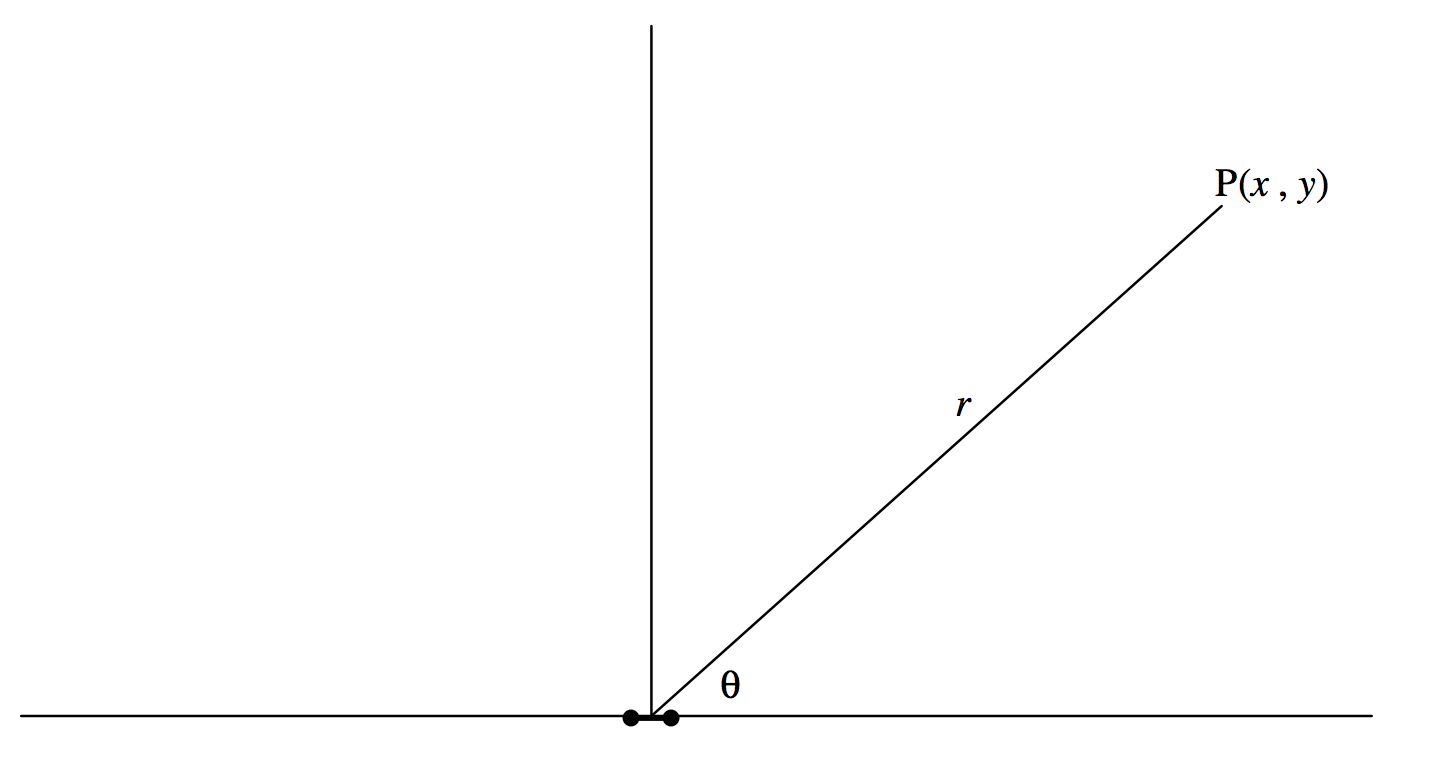
FIGURE III.8
and, with L2<<r2, the expression 3.7.5 for the potential at P becomes
V=Q4πϵ0(1(r2−2Lx)1/2−1(r2+2Lx)1/2)=Q4πϵ0r((1−2Lx/r2)−1/2−(1+2Lx/r2)−1/2).
When this is expanded by the binomial theorem we find, to order L/r , that the potential can be written in any of the following equivalent ways:
V=2QLx4πϵ0r3=px4πϵ0r3=pcosθ4πϵ0r2=p⋅r4πϵ0r3.
Thus the equipotentials are of the form
r2=ccosθ,
where
c=p4πϵ0V.
Now, bearing in mind that r2+x2+y2, we can differentiate V=px4πϵ0r3 with respect to x and y to find the x- and y-components of the field. Thus we find that
Ex=p4πϵ0(3x2−r2r5) and Ey=pxy4πϵr5.
We can also use polar coordinates to find the radial and transverse components from Er=−∂V∂r and Eθ=−1r∂V∂θ together with V=pcosθ4πϵ0r2 to obtain
Er=2pcosθ4πϵ0r3,Eθ=psinθ4πϵ0r3 and E=p4πϵ0r3√1+3cos2θ.
The angle that E makes with the axis of the dipole at the point (r,θ) is θ+tan−112tanθ.
For those who enjoy vector calculus, we can also say E=−14πϵ0∇(p⋅rr3), from which, after a little algebra and quite a lot of vector calculus, we find
E=14πϵ0(3(p⋅r)rr5−pr3).
This equation contains all the information that we are likely to want, but I expect most readers will prefer the more explicit rectangular and polar forms of equations ??? and ???.
Equation ??? gives the equation to the equipotentials. The equation to the lines of force can be found as follows. Referring to Figure III.9, we see that the differential equation to the lines of force is
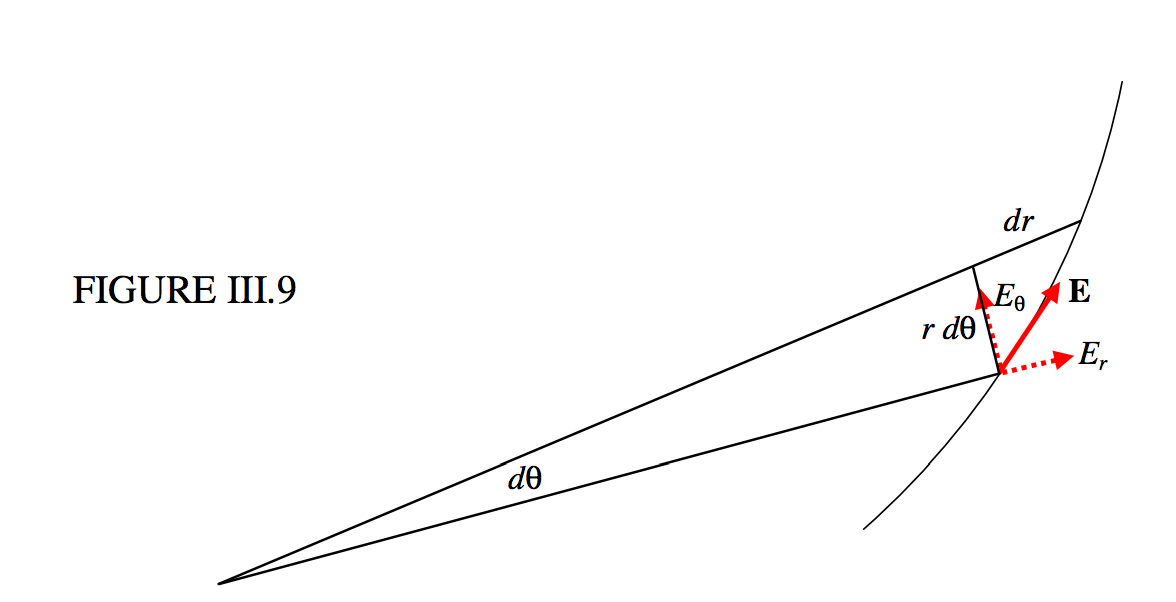
FIGURE III.9
rdθdr=EθEr=sinθ2cosθ=12tanθ,
which, upon integration, becomes
r=asin2θ.
Note that the equations r2=ccosθ (for the equipotentials) and r=asin2θ (for the lines of force) are orthogonal trajectories, and either can be derived from the other. Thus, given that the differential equation to the lines of force is rdθdr=12tanθ with solution r=asin2θ, the differential equation to the orthogonal trajectories (i.e. the equipotentials) is −1rdrdθ=12tanθ, with solution r2=ccosθ.
In Figure III.10, there is supposed to be a tiny dipole situated at the origin. The unit of length is L, half the length of the dipole. I have drawn eight electric field lines (continuous), corresponding to a = 25, 50, 100, 200, 400, 800, 1600, 3200. If r is expressed in units of L, and if V is expressed in units of Q4πϵ0L, the equations ??? and ??? for the equipotentials can be written , r=√2cosθV, and I have drawn seven equipotentials (dashed) for V = 0.0001, 0.0002, 0.0004, 0.0008, 0.0016, 0.0032, 0.0064. It will be noticed from Equation ???, and is also evident from Figure III.10, that Ex is zero for θ=54∘44′.
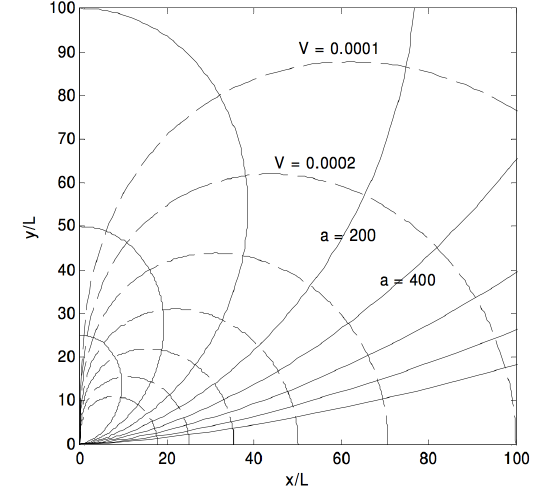
FIGURE III.10
At the end of this chapter I append a (geophysical) exercise in the geometry of the field at a large distance from a small dipole.
Equipotentials near to the dipole
These, then, are the field lines and equipotentials at a large distance from the dipole. We arrived at these equations and graphs by expanding Equation ??? binomially, and neglecting terms of higher order than L/r. We now look near to the dipole, where we cannot make such an approximation. Refer to Figure III.7.
We can write Equation ??? as
V(x,y)=Q4πϵ0(1r1−1r2),
where r21=(x−L)2+y2 and r22=(x+L)2+y2. If, as before, we express distances in terms of L and V in units of Q4πϵ0L, the expression for the potential becomes
V(x,y)1r1−1r2,
where r21=(x+1)2+y2 and r22=(x−1)2+y2.
One way to plot the equipotentials would be to calculate L for a whole grid of (x,y) values and then use a contour plotting routine to draw the equipotentials. My computing skills are not up to this, so I’m going to see if we can find some way of plotting the equipotentials directly.
I present two methods. In the first method I use Equation ??? and endeavour to manipulate it so that I can calculate y as a function of x and L. The second method was shown to me by J. Visvanathan of Chennai, India. We’ll do both, and then compare them.
First Method.
To anticipate, we are going to need the following:
r21r22=(x2+y2+1)2−4x2=B2−A,r21+r22=2(x2+y2+1)=2B,andr41+r42=2[(x2+y2+1)2+4x2]=2(B2+A),whereA=4x2andB=x2+y2+1
Now Equation ??? is r1r2V=r2−r1. In order to extract y it is necessary to square this twice, so that r1 and r2 appear only as r21 and r22. After some algebra, we obtain
r21r22[2−V4r21r22+2V2(r21+r22)]=r41+r42.
Upon substitution of equations 3.7.18,17,18, for which we are well prepared, we find for the equation to the equipotentials an equation which, after some algebra, can be written as a quartic equation in B:
a0+a1B+a2B2+a3B3+a4B4=0wherea0=A(4+V4A),a1=4V2A,a2=−2V2A,a3=−4V2,anda4=V4.
The algorithm will be as follows: For a given V and x, calculate the quartic coefficients from equations 3.7.26-3.7.30. Solve the quartic Equation 3.7.25 for B. Calculate y from Equation 3.7.22. My attempt to do this is shown in Figure III.11. The dipole is supposed to have a negative charge at (−1 , 0) and a positive charge at (+1 , 0). The equipotentials are drawn for V = 0.05, 0.10, 0.20, 0.40, 0.80.
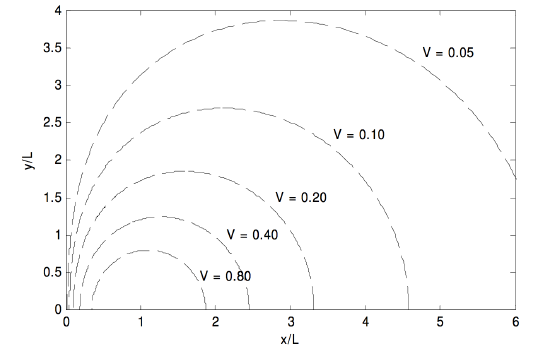
FIGURE III.11
Second method (J. Visvanathan).
In this method, we work in polar coordinates, but instead of using the coordinates (r,θ), in which the origin, or pole, of the polar coordinate system is at the center of the dipole (see Figure III.7), we use the coordinates (r1,ϕ) with origin at the positive charge.
From the triangle, we see that
r22=r21+4L2+4Lr1cosϕ.
For future reference we note that
∂r2∂r1=r1+2Lcosϕr2.
Provided that distances are expressed in units of L, these equations become
r22=r21+4r1cosϕ+4,
∂r2∂r1=r1+2cosϕr2.
If, in addition, electrical potential is expressed in units of Q4πϵ0L, the potential at P is given, as before (Equation ???), by
V(r1,ϕ)=1r1−1r2.
bearing in mind that r2 is given by Equation ???.
By differentiation with respect to r1, we have
f′(r1)=−1r21+1r22∂r2∂r1=−1r21+r1+2cosϕr32,
and we are all set to begin a Newton-Raphson iteration: r1=r1−f/f′. Having obained r1, we can then obtain the (x,y) coordinates from x=1+r1cosφ and y=r1sinφ.
I tried this method and I got exactly the same result as by the first method and as shown in Figure III.11.
So which method do we prefer? Well, anyone who has worked through in detail the derivations of equations 3.7.18 -3.7.30, and has then tried to program them for a computer, will agree that the first method is very laborious and cumbersome. By comparison Visvanathan’s method is much easier both to derive and to program. On the other hand, one small point in favor of the first method is that it involves no trigonometric functions, and so the numerical computation is potentially faster than the second method in which a trigonometric function is calculated at each iteration of the Newton-Raphson process. In truth, though, a modern computer will perform the calculation by either method apparently instantaneously, so that small advantage is hardly relevant.
So far, we have managed to draw the equipotentials near to the dipole. The lines of force are orthogonal to the equipotentials. After I tried several methods with only partial success, I am grateful to Dr Visvanathan who pointed out to me what ought to have been the “obvious” method, namely to use Equation ???, which, in our (r1,ϕ) coordinate system based on the positive charge, is r1dϕdr1=EϕEr1, just as we did for the large distance, small dipole, approximation. In this case, the potential is given by equations ??? and ???. (Recall that in these equations, distances are expressed in units of L and the potential in units of Q4πϵ0L.) The radial and transverse components of the field are given by Er1=−∂V∂r1 and Eϕ=−1r1∂V∂ϕ, which result in
Er1=1r21−r1+2cosϕr32
and
Eϕ=2sinϕr32.
Here, the field is expressed in units of Q4πϵ0L2, although that hardly matters, since we are interested only in the ratio. On applying r1dϕdr=EϕEr1 to these field components we obtain the following differential equation to the lines of force:
dϕ=2r1sinϕ(r21+4+4r1cosϕ)3/2−r21(r1+2cosϕ)dr1.
Thus one can start with some initial φ0 and small r2 and increase r1 successively by small increments, calculating a new φ each time. The results are shown in Figure III.12, in which the equipotentials are drawn for the same values as in Figure III.11, and the initial angles for the lines of force are 30º, 60º, 90º, 120º, 150º.
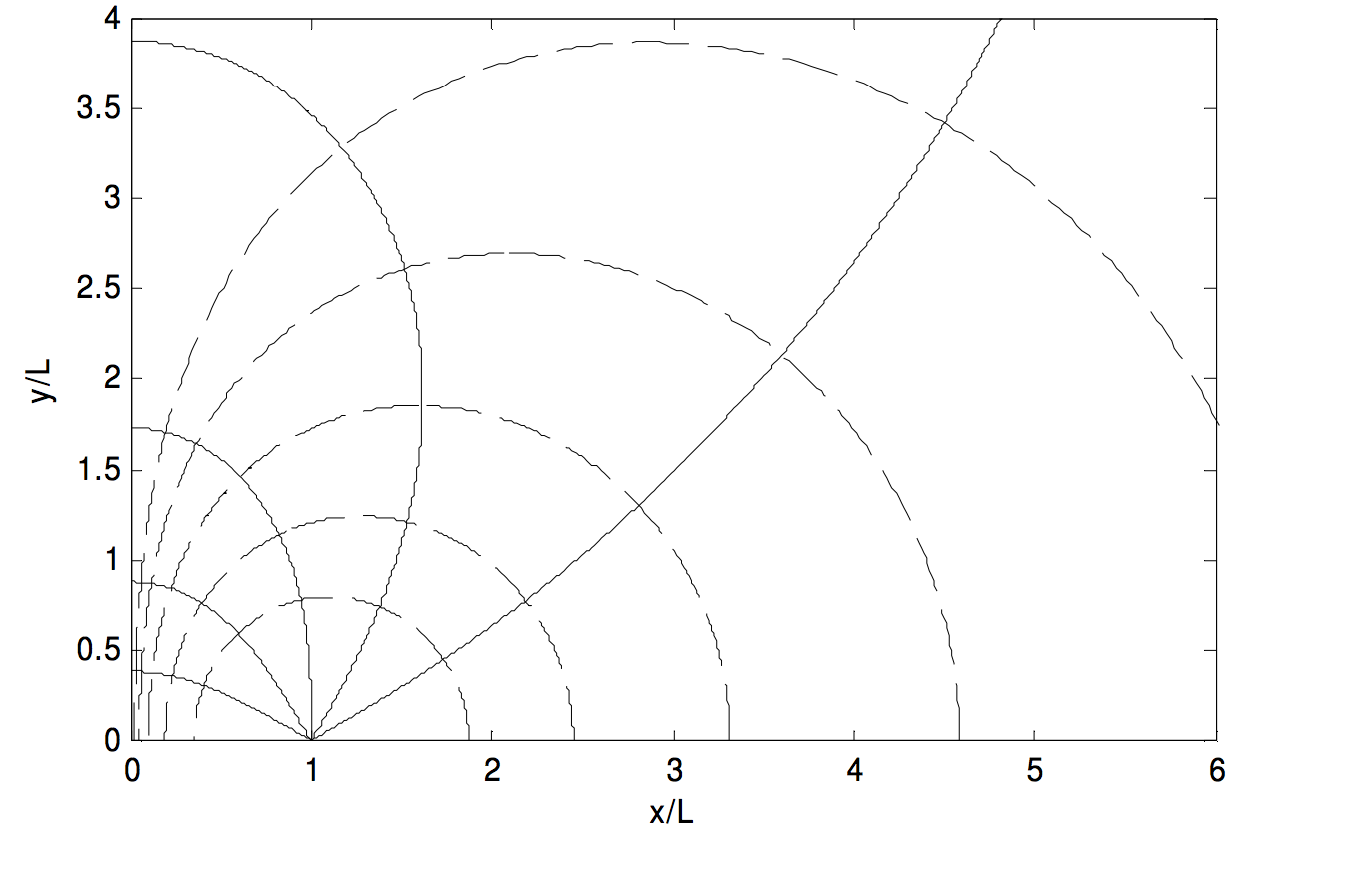
FIGURE III.12
Before we leave this section, here is yet another method of calculating the potential near to a dipole, for those who are familiar with Legendre polynomials.
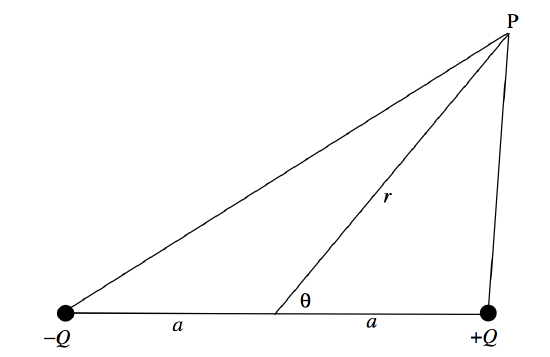
The potential at P is given by
4πϵ0V=Q[1(a2+r2−2arcosθ)1/2−1(a2+r2+2arcosθ)1/2]=Qa[1(1−2ρcosθ+ρ2)1/2−11+2ρcosθ+ρ2)1/2]
where ρ=r/a.
It is well known (to those who are familiar with Legendre polynomials!) that
(1−2ρcosθ+ρ2)−1/2=P0(cosθ)+P1(cosθ)ρ+P2(cosθ)ρ2+P3(x)ρ3+...
where the Pn are the Legendre polynomials. Thus the potential can be calculated as a series expansion. Those who are unfamiliar with the Legendre polynomials can find something about them in my notes on celestial mechanics www.astro.uvic.ca/~tatum/celmechs/celm1.pdf


