1.6: Motion in Multiple Dimensions
( \newcommand{\kernel}{\mathrm{null}\,}\)
Now that we have mastered the simplest form of motion, it’s time to branch out to more general cases. No longer will the motion of objects be constrained to move along a straight line! Of course, this means that we can no longer allow simple positive and negative values to tell us about directions – we need to introduce vectors into the story. Fortunately, we have built our vector mathematics tools to the point where we can make use of them here.
Position and Displacement
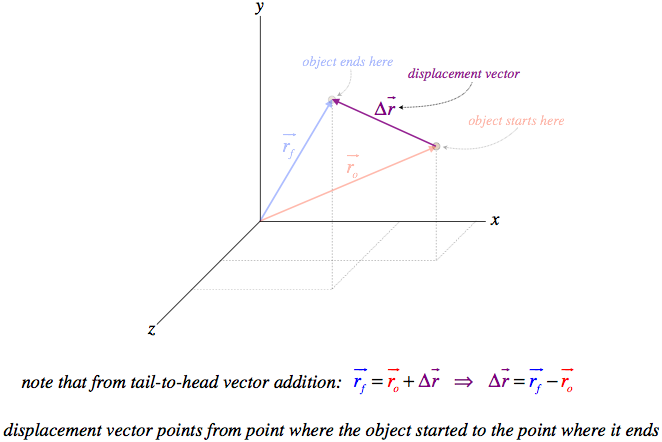
Without the luxury of being able to describe the position of an object with a single (positive or negative) value, we now have to do so in terms of something called a position vector. If we assume a coordinate system is in place, the position of the object can be described by its coordinates, x, y, and z. These also happen to be the components of the position vector, which we define as the vector that points from the origin to the point in space:
If an object moves from one position to another, then clearly it is displaced, and we can describe this displacement in terms of the change of the position, as we did for straight-line motion. The only difference is that here we create a displacement vector:
Δ→r=→rf−→ro=(xf−xo)ˆi+(yf−yo)ˆj+(zf−zo)ˆk
Figure 1.6.1 – Displacement Vector

Velocity
We follow the same process as we did with straight-line motion to determine average and instantaneous velocity vectors. Namely, we define the average and instantaneous velocities in terms of the rate of change of the displacement:
→vave=Δ→rΔt=ΔxΔtˆi+ΔyΔtˆj+ΔzΔtˆk
→v=d→rdt=dxdtˆi+dydtˆj+dzdtˆk
While this vector formula might appear to imply that the direction of the velocity vector is the same as the direction of the position vector, it's important to understand that in fact the direction of the velocity vector is the same as the direction of the infinitesimal change of the position vector. Let's look at an example that makes this clear...
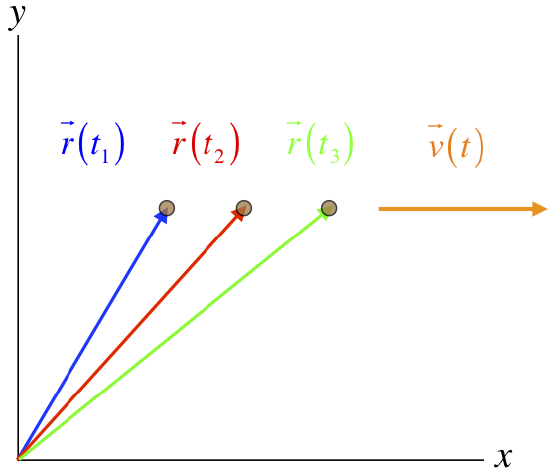
Consider a particle moving in the x−y plane. Its time-dependent position vector can be expressed in terms of its time-dependent components as:
→r(t)=x(t)ˆi+y(t)ˆj
For the sake of this example, let's suppose that the particle's position components have the following time dependences:
x(t)=(3.0ms)ty(t)=5.0m
Now we can calculate the velocity vector by taking the time derivative of the position vector. The unit vectors ˆi and ˆj don't change with time, so the derivative is simply:
→v(t)=ddt→r=[ddtx(t)]ˆi+[ddty(t)]ˆj=(3.0ms)ˆi
The position vector changes in both magnitude and direction, while the velocity vector does neither. This demonstrates that the formula that relates the position and velocity vectors might appear to imply some kinship between these vectors, but in fact the presence of the derivative removes the possibility of generalizations like them pointing in the same direction. A diagram of this example for three different times should help visualize this difference:
Figure 1.6.2 – Comparison of a Position Vector and the Related Velocity Vector
Acceleration
Naturally acceleration works the same way as velocity in terms of the calculus:
→aave=Δ→vΔt=ΔvxΔtˆi+ΔvyΔtˆj+ΔvzΔtˆk
→a=d→vdt=dvxdtˆi+dvydtˆj+dvzdtˆk
Alert
Notice that if we confine ourselves to motion in just one dimension (say the x-axis), then we get exactly the equations we obtained in Section 1.3. So what motion in three dimensions amounts to is additional bookkeeping – we have three separate sets of kinematic relations to keep track of, instead of only one.
Splitting Direction and Magnitude – Velocity
Alert
Students occasionally struggle with what follows, perhaps because the idea of a unit vector is still a bit abstract to them. If you find yourself in this situation, you should spend a little extra time to become comfortable with these ideas, as they are central to everything that follows in this course.
We know that whenever we take the derivative of a vector like position (to obtain velocity) or velocity (to obtain acceleration), a non-zero result comes about when that vector is changing in some way (magnitude, direction, or both). Let’s see what happens if we split these two vector properties up and treat them separately...
The unit vectors we have encountered to this point have been exclusively the cartesian unit vectors – those that point in the x, y, and z directions: ˆi, ˆj, and ˆk. When we first encountered unit vectors, we saw that a vector can be written as a product of its magnitude and the unit vector that points in its direction (Equation 1.1.2). If this vector happens to be changing direction over time, then unlike the cartesian unit vectors, this unit vector changes over time. As a first example, let's look at what this means for the position vector (the derivative of which is the velocity vector). We know how to express the position vector in terms of cartesian unit vectors (Equation 1.6.1), but in terms of its magnitude and directional unit vector, it is written in the same manner as Equation 1.1.2}:
Recall that when a vector's variable name (in this case, r) is written without the arrow over it, it refers to the magnitude of the vector. In this case, this magnitude is, in terms of the cartesian components:
r=√x2+y2+z2
Referring back to Figure 1.6.2, we see a case where both the magnitude and direction of the position vector are changing. Therefore when we compute the velocity vector, the derivative will act on both the magnitude and on the unit vector, and it turns out that the usual product rule works perfectly well here:
→v=ddt→r=ddt(rˆr)=drdtˆr+rdˆrdt
Alert
This was just stated above, but it bears repeating... The cartesian unit vectors ˆi, ˆj, and ˆk don't change with time (they always point in the x, y, and z directions), but other unit vectors (like ˆr) can and do change with time, so their derivatives don't automatically vanish. It is the derivative of this unit vector that determines how that vector's direction is changing.
Okay, so let's consider the following questions:
Example 1.6.1
How is Equation 1.6.9 affected when the object happens to be moving either directly toward or directly away from the origin?
- Solution
-
If the object is moving directly toward or away from the origin, then the position vector (whose tail is at the origin and head is at the object) is always pointing in the same direction, but never changes direction. Therefore the second term in that equation vanishes, leaving only the first term.
Example 1.6.2
How is Equation 1.6.9 affected when the object happens to be moving such that its distance from the origin never changes?
- Solution
-
If the object's distance from the origin never changes, then the magnitude of the position vector is not changing, which means that the first term vanishes. Clearly in order to move while staying the same distance from the origin, the direction of motion must be changing, so the second term is not zero.
But wait, an object moving such that its distance from a single point never changes must be traveling in a circle (assuming its motion remains in a plane). So this velocity vector is that of circular motion around the origin. A general velocity vector (one in which neither term from the product rule vanishes) can therefore be thought of as a vector sum of a velocity vector that points radially outward from an origin, and one that points tangent to a circle centered at that origin. Geometrically, it looks like this:
Figure 1.6.3 – Parallel and Perpendicular Components
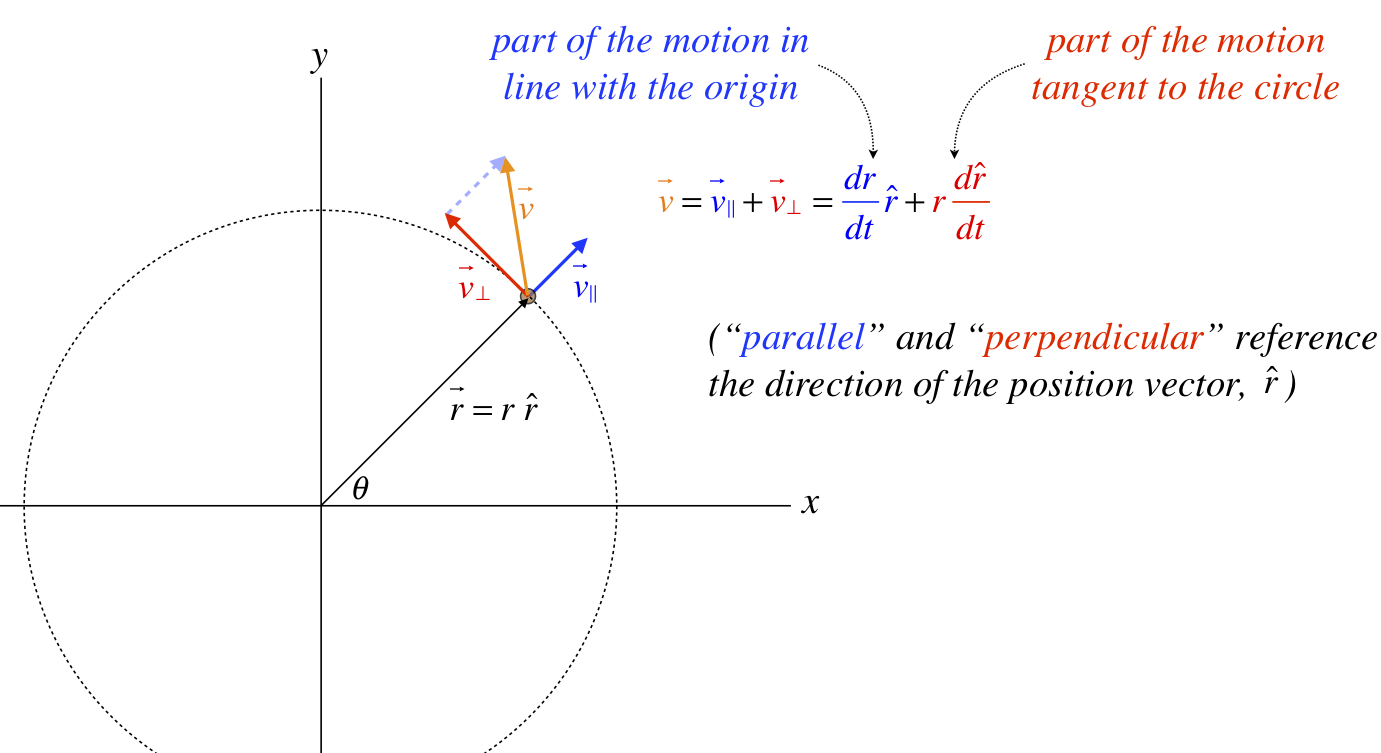
Clearly the derivative of the position unit vector is a new vector that is perpendicular to the position unit vector. We can check to see if this is true, as well as make sense of all this by returning to the easier-to-work-with cartesian unit vector approach. We do this by writing the position vector in polar coordinates. Using θ as the angle in the diagram above, we use trigonometry to break the position vector into x and y components, written in terms of r and θ:
→r=rcosθˆi +rsinθˆj
Combining this with Equation 1.6.1 and Equation 1.6.7 gives us the position unit vector in terms of the cartesian unit vectors:
It's easy to confirm that this unit vector has a length of 1, as it should. The claim above is that the time derivative of ˆr is perpendicular to ˆr itself, which we can now check directly, using our clever tool from Section 1.2 – the scalar product of these two vectors should vanish. Start by computing the derivative of the position unit vector. The cartesian unit vectors have zero derivative, but of course θ can be changing as the object moves, so:
dˆrdt=ddt(cosθˆi +sinθˆj)=−sinθ(dθdt)ˆi+cosθ(dθdt)ˆj=dθdt(−sinθˆi+cosθˆj)
Now perform the dot product:
ˆr⋅dˆrdt=(cosθˆi +sinθˆj)⋅[dθdt(−sinθˆi+cosθˆj)]=dθdt(−cosθsinθ+sinθcosθ)=0
Example 1.6.3
Show that the time derivative of any unit vector is either zero (as in the case of ˆi) or is perpendicular to the unit vector itself (as in the case of ˆr). [Hint: The product rule for the derivative works for the scalar product.]
- Solution
-
Naturally the derivative of the number 1 is zero, and this happens to be the result of a scalar product of a unit vector with itself, so applying the product rule:
0=ddt(1)=ddt(ˆA⋅ˆA)=dˆAdt⋅ˆA+ˆA⋅dˆAdt=2ˆA⋅dˆAdt
This can only equal zero if the vector resulting from the derivative is zero, or it is perpendicular to ˆA.
Splitting Direction and Magnitude – Acceleration
Above we found that a velocity vector can be broken into two components – one parallel to the position vector and one perpendicular to it. The first accounts for velocity in line with the origin, and the second for velocity tangent to a circle around the origin. This has few applications in physics, because typically the choice of origin is arbitrary. But when we extend the use of this vector calculus machinery to acceleration, it gets more interesting and far more useful, as we will see.
If we replace the position vector with the velocity vector and follow the same procedure as above, we get for the acceleration:
→a=ddt→v=ddt(vˆv)=dvdtˆv+vdˆvdt
Once again we see that the product rule separates the derivative into a sum of two vectors – one that is parallel to the original velocity, and one that is perpendicular to it. For future reference, we'll write the two terms this way:
→a∥≡dvdtˆv→a⊥≡vdˆvdt
We already know that the acceleration vector is the rate of change of the velocity vector, and that the velocity vector includes the speed and direction of motion, so here we see that the acceleration breaks into two vectors: →a||, which handles only the change of speed, and →a⊥, which handles only the change of direction. If only the first term is non-zero, then the object is speeding up or slowing down in a straight line. If only the second term is non-zero, then the object is neither speeding-up nor slowing down, but its direction of motion is changing. We will get a lot of mileage out of this division of labor in the chapters to come.
Example 1.6.4
A particle moves through space with a velocity vector that varies with time according to:
→v(t)=αˆi−βtˆj,
where α and β are positive constants. Find the rate at which the speed of this particle is changing at time t=0. Does this rate remain the same for all later times?
- Solution
-
Acceleration is the rate of velocity change, which can come in the form of speed change or direction change (or both). This problem asks specifically for the rate of change of the speed. Let's start by computing the acceleration vector:
→a(t)=ddt→v(t)=−βˆj
One's first inclination might be to state that the magnitude of the acceleration is β, and there is no time dependence, so the speed is changing at this rate at all times. But we must be careful to only consider the part of the acceleration vector that describes speed change, and not direction change. We know that the parallel part of the acceleration deals with speed change, so we need a way to extract this piece from the full acceleration vector. But we know how to extract the part of one vector parallel to another, using the scalar product. Namely:
a∥=→a⋅ˆv=→a⋅→vv=(−βˆj)⋅(αˆi−βtˆj√α2+β2t2)=β2t√α2+β2t2
Plugging in t=0 reveals that the particle is not speeding up at all at that time. We also see this does not remain true for all values of t. The reason is that the acceleration vector is a constant, and is initially perpendicular to the velocity vector, so at that moment it can only change its direction. When the velocity vector changes direction, this new direction has a component parallel to the unchanging acceleration vector, which means the particle speeds up.


