1.1: The Relativity Principle
( \newcommand{\kernel}{\mathrm{null}\,}\)
Inertial Frames
Back in our studies of classical mechanics, we spent a very brief period of time learning about how to relate the measurements of position and time between two observers in relative motion (go here for the LibreText reminder of this topic). Actually "relative motion" in this context is imprecise. We restricted our study to a very specific kind of relative motion – that for which the two observers maintain a constant relative velocity.
For what is to come, we will restrict these frames of reference even further – we will insist that every observer makes its measurements from an inertial frame. This kind of frame is one in which Newton's first law assures that objects will not spontaneously begin to accelerate. That is, if we are in such a frame, and we eliminate all of the real forces present on a stationary object, then the object remains at rest in that frame.
The simplest way to understand inertial frames is to consider what kind of frame is not inertial. Suppose you are in spaceship (far away from all gravitational sources), and it is accelerating forward. You hold a pencil in your hand, which is at rest in your frame, but you are exerting a force on it with your fingers, so to test to see if you are in an inertial frame, you release it. As soon as you do, it continues with whatever speed it had at the moment of release, while you and your spaceship continue to accelerate. From your perspective, it is the pencil that accelerates, which tells you that you are not in an inertial frame.
[One might wonder why an inertial frame is an additional restriction beyond what we did in 9A. Certainly the intention was to deal with inertial frames back then, but technically two frames with equal acceleration vectors (but unequal velocities) will also satisfy the Galilean transformation.]
Postulate(s)
We have a simple experiment for testing whether our frame is inertial, but it doesn't tell us whether our frame is stationary or moving in a straight line at a constant speed, because when we release the pencil under these circumstances, it remains stationary from our perspective in both cases. So what kind of experiment will tell us whether or not we are moving?
Albert Einstein pondered this very thought, and came up with no answer. Eventually, he felt compelled to assert it as a fundamental aspect of our universe, and the relativity principle was born:
No experiment can be performed within an inertial frame that determines whether it is moving or at rest.
This is also known as the first postulate of the theory of Special Relativity. One way that we can express this is in terms of an "argument" between two observers.
Figure 1.1.1 – All Observers in Inertial Frames Can Claim to Be Stationary
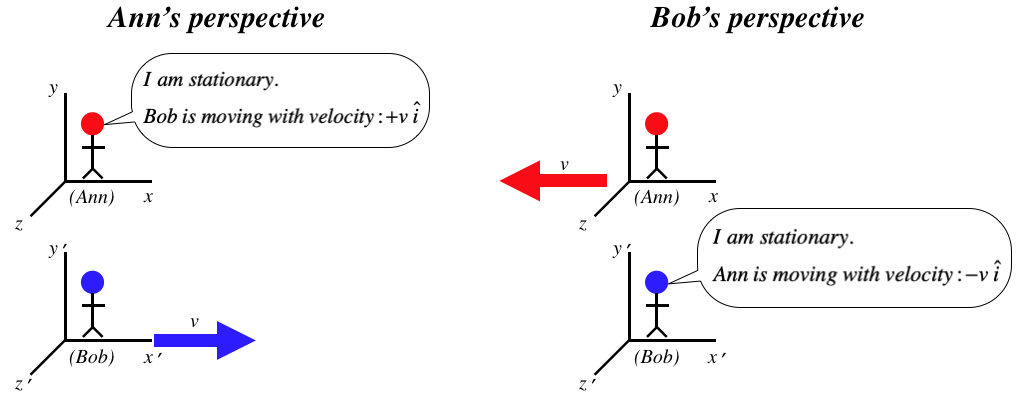
[These kinds of diagrams, where the perspectives of two observers in relative motion, will have some common elements. First, we will always define their relative motion to be parallel to their common x-axes. Second, we will define the primed frame to be moving in the +x direction relative to the unprimed frame.]
Calling this the "first postulate" implies that there is a second postulate, and there is, though one could argue that it follows directly from the first postulate and therefore doesn't need to be stated separately. It is this:
Every observer measures the velocity light to be the same value.
The reason this "second postulate" can be considered a consequence of the first postulate is that the theory from which we derive the speed of light contains no provisions for the motion of the observer (or rather, it predicts the same speed for all observers). Therefore the theory predicts that any experiment that measures the speed of light in a vacuum will give a specific answer. If different inertial frames produced different values for the speed of light, we would have a violation of the first postulate, as we would then have an experiment to determine the "true" rest frame. So to the extent that we accept this theory of light propagation, we don't need the second postulate.
Digression: "Ultimate Speed"
The discussion above actually paints a somewhat in inaccurate picture of the foundation of relativity. As we will see later, these postulates lead to the requirement of the speed of light being the limit which no relative motion can ever exceed. It turns out that if we just postulate that such an "ultimate speed" exists, then relativity results, independent of the theory of light propagation. That is, light sort of "coincidentally" travels at the ultimate speed, but the theory of relativity would apply even it if didn't, so long as this "cosmic speed limit" exists.
A Bit About Waves
The first postulate seems innocuous enough, and perhaps it even seems intuitive. But this business about every observer measuring the same speed for a beam of light didn't sit well with many physicists at the time Einstein proposed it. To see why, and to fully understand the implications of this being true, we need to review a little bit about waves, because as we know from Physics 9B and 9C, light is a wave phenomenon. Of all the things we previously learned about waves, these are the properties of waves we will most need to recall for this discussion...
effect of medium
Waves are phenomena which transfer energy through space by the means of a self-propagating disturbance of a medium (the stuff that is "waving"). A wave on a string carries energy along because a piece of the string displaces, which pulls on an adjacent piece of string, displacing it, and so on. Surface waves on water and sound waves through air work in a similar manner. What these all have in common is that medium itself doesn't travel with the energy (it moves with the disturbance), and the speed with which adjacent particles in the medium interact with each other is a property of the medium. Put another way, the speed of a wave is exclusively a function of the properties of the medium. A wave on a string travels faster when the string is more taut, and slower when the string is made is more dense, for example.
superposition
When two waves traveling through the same medium encounter each other, the effects they have on the medium are additive at that the same point in the medium. So if one wave displaces a string by y1 at some position x on the string, and another wave displaces the string by y2 at the same position, then the total displacement of the string with the two waves present at x at the same time is y1+y2. This additivity property is called superposition, and it has the particularly interesting feature that two waves can actually cancel each other entirely (a phenomenon called destructive interference), if the two waves happen to be displacing the medium equal amounts in opposite directions.
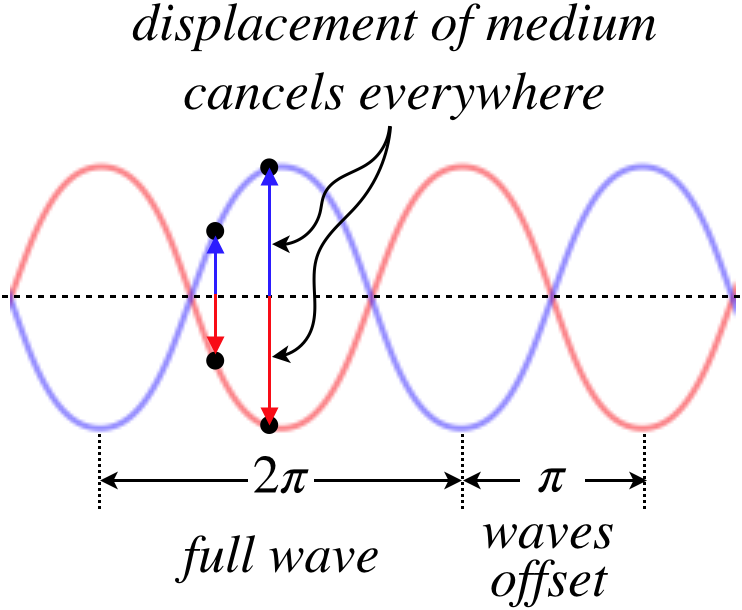
If a wave happens to be harmonic (the medium displacement as a function of position and time is a sine wave), then this destructive interference occurs when two identical waves are out of phase by π.
Figure 1.1.2 – Destructive Interference of Two Harmonic Waves
The Michelson-Morley Experiment
The crux of the problem for those originally opposed to Einstein's assertion that the speed of light is the same when measured by any observer is that this is not true of other waves. If one moves through the air into an oncoming sound wave, that sound wave is moving faster relative to that person than relative to someone stationary in the air. The point is that, as stated above, the speed of a wave is entirely determined by the medium, and this speed is relative to that medium. So if an observer moves relative to a medium, then the relative speed of waves propagating through that medium can change.
So we are left with the question: What medium is disturbed as a light wave passes through it, and can't we see a change in the speed of light if we just move relative to this medium? This was an open question at the time of Einstein, and was very puzzling for a couple reasons. The first is that the theory of light did not require the existence of any medium at all.
But far more puzzling than this was the fact that no one could seem to come up with any experimental evidence of the existence of a medium for light (which they referred to as the luminiferous aether). The most convincing null result of such a search was performed by two American physicists Albert Michelson and Edward Morley, who employed a device called an interferometer, the basics of which are still used today for countless applications.
The basics of an interferometer work like this: A single light beam is split into two separate beams. As they came from the same source, they are in phase with each other, but if we send them on separate journeys, and then bring them back together, they may no longer be in phase. For example, one of the beams may travel farther than the other. If the difference in their phases when they get back together is just right, they will destructively interfere with each other.
[For the two beams to behave this way, the original beam needs to be somewhat coherent, meaning that parts of the light near each other are in phase. Nowadays we easily achieve this artificially with lasers (sunlight is also quite coherent), but fortunately the degree of coherence achievable in a lab in the late 1800's was sufficient to successfully perform this experiment.]
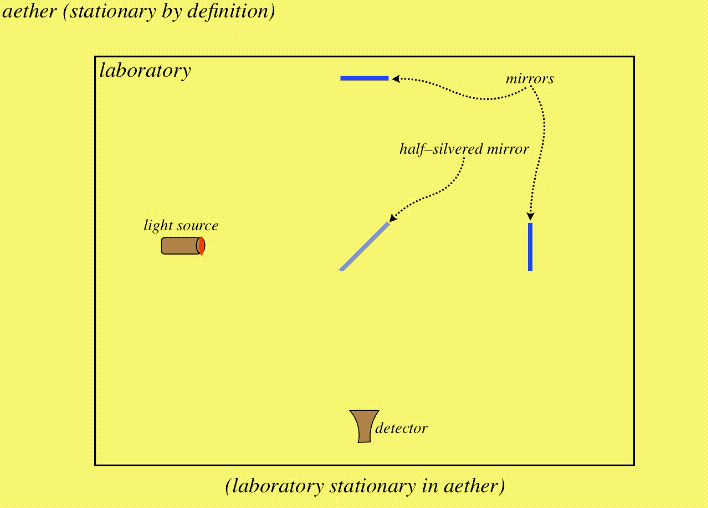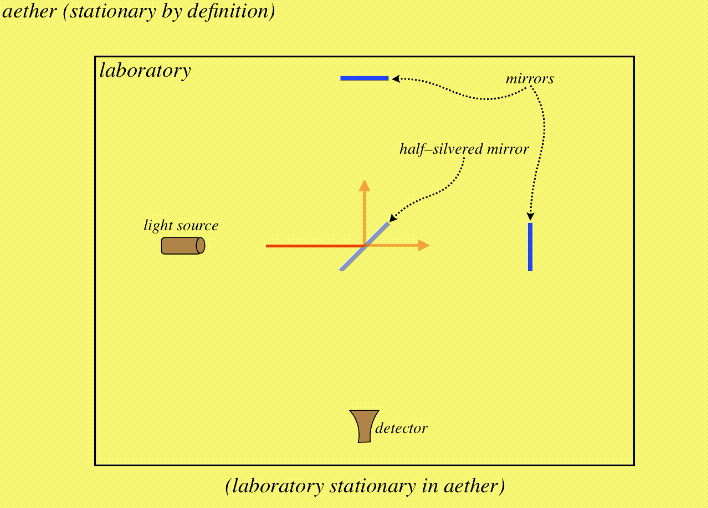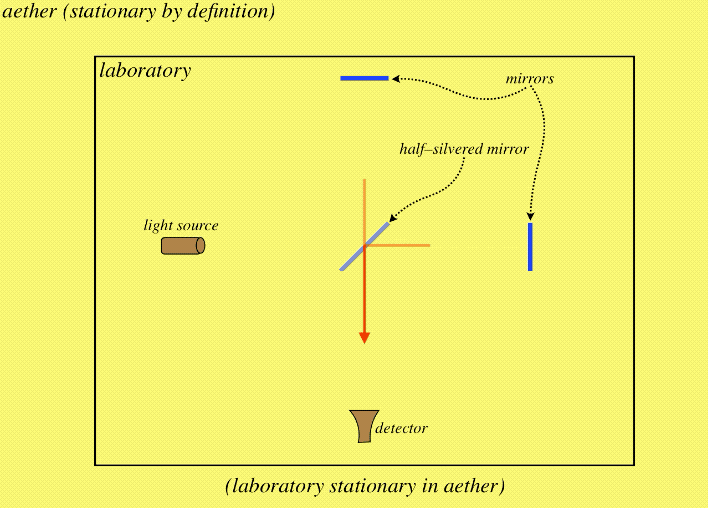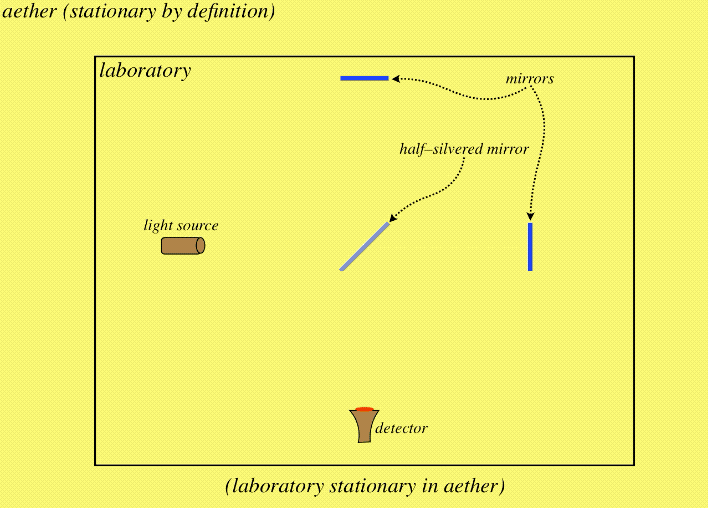
The ingenuity of the MM interferometer is that it splits the beam of light and sends the two pieces on journeys that are equal distances, but are at right angles to each other. If the laboratory is stationary in the aether, then the beams come back to the detector in phase, and do not cancel each other out:
Figure 1.1.3 – Laboratory Stationary in Aether
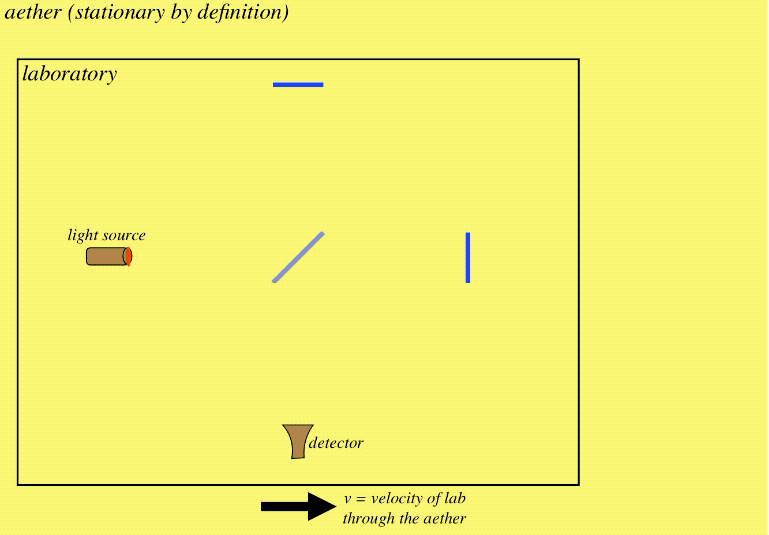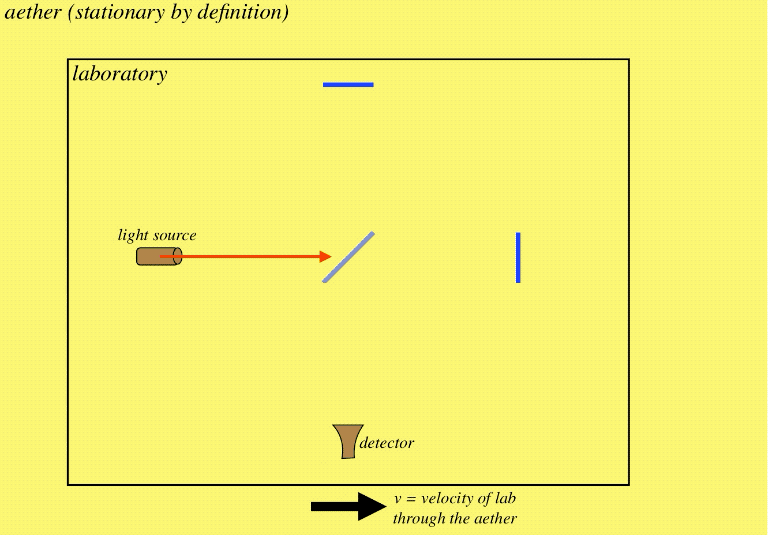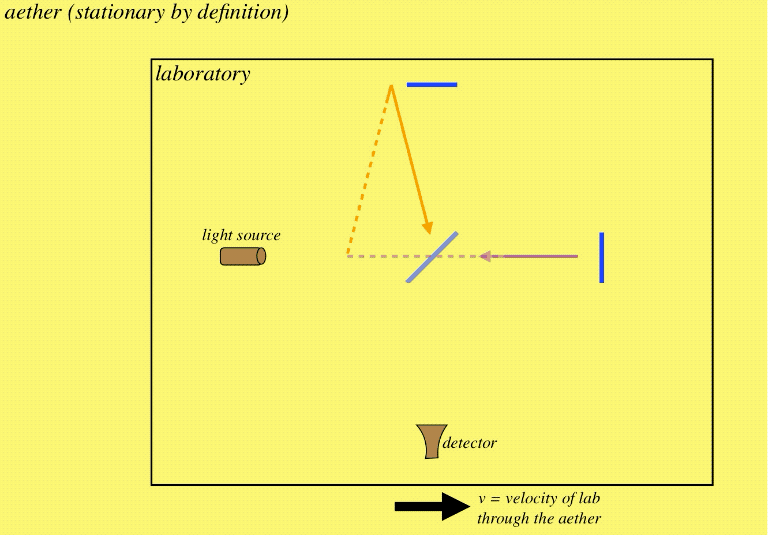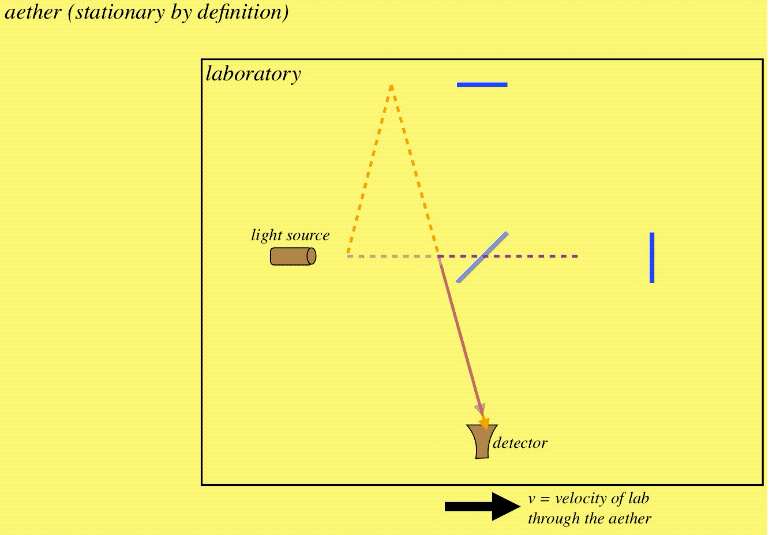
If this device is moving through aether (let's say in a direction parallel to one of these directions), then one of the arms of the interferometer moves parallel to the direction of the light during the journey, while the other moves perpendicular to it. These two journeys are not equal in distance, which means the beams can enter the detector out of phase:
Figure 1.1.4 – Laboratory Moving through Aether
We can do a bit of math to determine the difference in the distance between these two journeys. The only difference between the paths of the two beams comes after they encounter the half-silvered mirror the first time, and before they encounter it the second time, so we focus on this portion of the process for both of them:
Figure 1.1.5 – Distance Traveled by the Transverse Beam
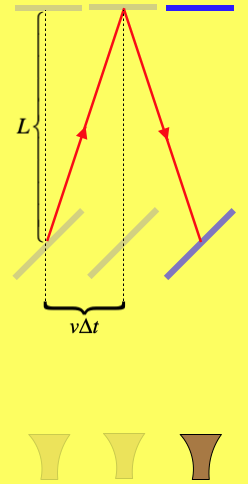
The transverse beam (the one perpendicular to the laboratory's motion) follows a diagonal path in both directions, the distance of which can be determined from the Pythagorean Theorem:
s=2√L2+(vΔt)2
But the distance traveled by the beam also equals the speed of light through the aether c multiplied by the time elapsed, so we get:
s=2cΔt⇒s=2√L2+(vs2c)2⇒s=2L√1−v2c2
Figure 1.1.6 – Distance Traveled by the Longitudinal Beam
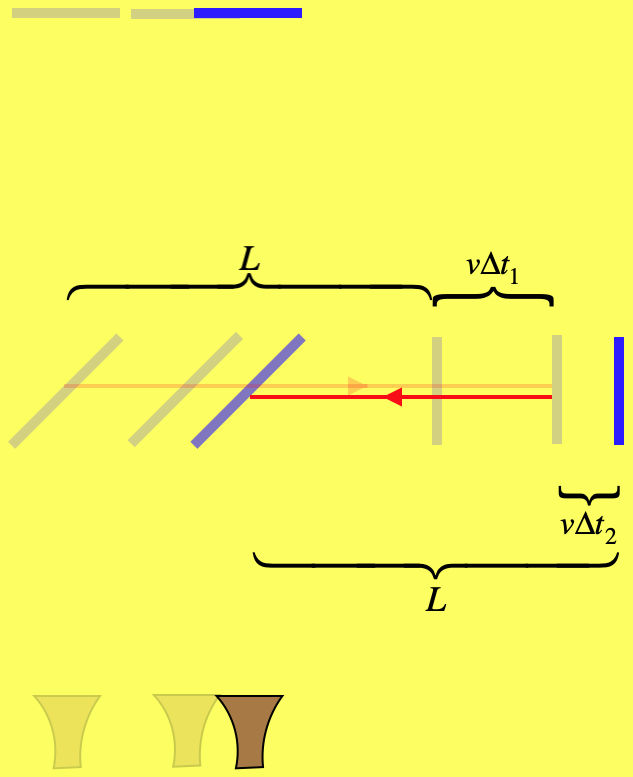
The longitudinal beam (the one parallel to the laboratory's motion) stays on a straight line, but the time it spends going in each direction is not the same, so we compute these times separately then use them along with the speed of light to get the full distance this beam traverses during this part of the process:
s1=L+vΔt1=cΔt1⇒Δt1=Lc−vs2=L−vΔt2=cΔt2⇒Δt2=Lc+v}Δt1+Δt2=2LCc2−v2⇒s=c(Δt1+Δt2)=2L1−v2c2
We can see from these two results that the two beams travel different distances. The denominator for each case is a fraction that is less than 1, so the square root is the larger denominator. This means that the longitudinal path (with the smaller denominator) is longer than the transverse path. The difference between these paths can be expressed by a multiplicative factor that depends upon the speed of the laboratory through the aether and the speed of light:
slongitudinal=1√1−v2c2stransverse
We therefore find that if the laboratory is moving through the aether at just the right speed, then the difference in distances traveled will equal half the length of a wave, and the two beams will cancel at the detector, resulting in darkness. In fact, this is not the only case that will give this result. If the difference in distance traveled is 32 of a full wave, then again the troughs and crests of the waves will match up, making destructive interference. Moreover, even if there is not complete destructive interference, every offset of the waves will result in some variation in the brightness of the light.
So given that the earth is moving through space, and is also rotating, one would expect that it is not difficult to find some evidence that the aether exists, and that we are moving through it. But try as they might, Michelson and Morley found no such thing. Many explanations were offered for the problem (many before the experiment was even performed), such as the aether being "dragged" by the earth, so that it was stationary around us here on the surface (logical arguments based on starlight observations and additional experiments on starlight proved this to be false). Einstein alone showed the courage to just discard the existence of the aether altogether, no matter how nonsensical the consequences might seem to be at first.
Analyze This
A

- Analysis
-
F


