1.4: Paradoxes
( \newcommand{\kernel}{\mathrm{null}\,}\)
The Ladder & Barn Paradox
We have derived some rather outlandish results from the postulate(s) of relativity, using the simple but powerful tool of thought experiments. We will now use that same tool to construct some scenarios that appear at first blush to result in logical inconsistencies in the theory called paradoxes, and then we will shoot them down, demonstrating that the theory is in fact logical and consistent.
The first paradox we will examine involves length contraction, and it goes like this...
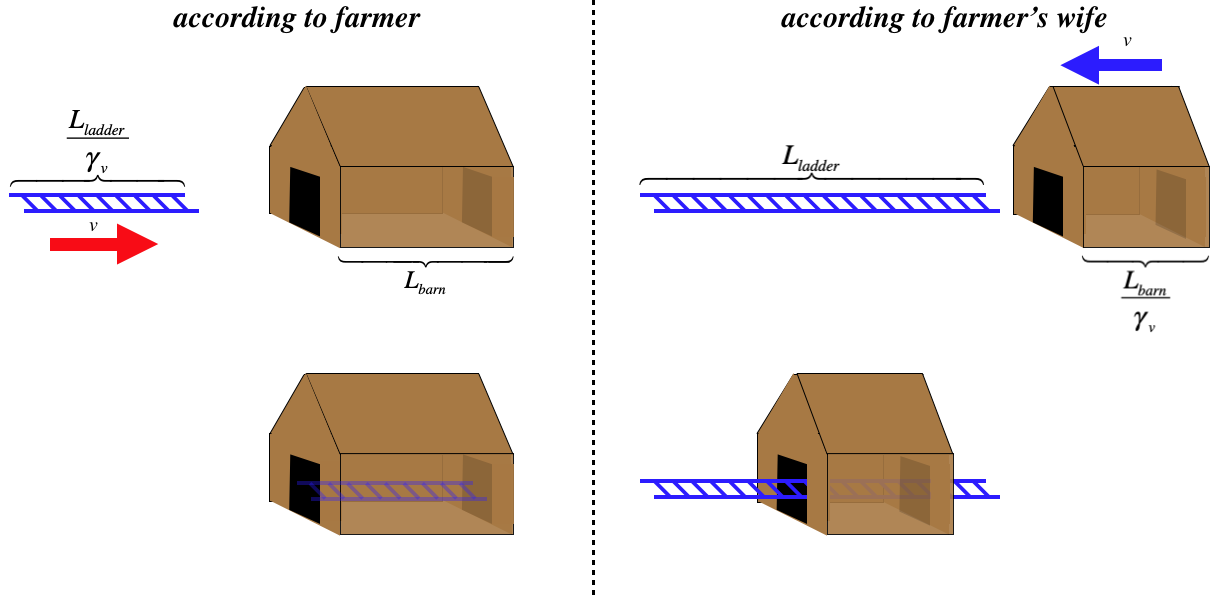
A farmer wishes to store a long ladder that he owns inside his barn, but is frustrated to discover that his ladder is too long to fit. Specifically, he finds that is ladder is 50ft long, while his barn is only 40ft long. But like every good farmer, this fellow is well-versed in special relativity, and decides that if he can get the ladder moving fast enough relative to the barn, then the ladder’s length will contract enough so that both the front and back barn doors can be closed at the same time while the ladder is inside. Before he actually tries to close the ladder in, he does a test run, zooming the ladder in one door and out the other. Sure enough, as his wife drives their souped-up tractor at 0.6c, he notes that both ends of the length-contracted ladder are briefly within the confines of the two doors:
farmer measures ladder length to be: L′=Lγv=√1−(0.6cc)2(50ft)=40ft
Since the 40ft barn is at rest relative to the farmer, the 40ft length-contracted ladder just barely fits.
Overjoyed that his ploy is going to work, he goes to embrace his wife, who looks distraught. When he asks her what is the matter, she says, “When I am zooming into the barn, it is way too short to fit the ladder." Indeed:
farmer's wife measures barn length to be: L′=Lγv=√1−(0.6cc)2(40ft)=32ft
The frame of the farmer's wife sees the ladder at rest and the barn moving past, so naturally the 50ft ladder doesn't fit inside the 32ft length-contracted barn. So how it is possible that both the farmer and his wife are correct at the same time? How can the ladder both be contained in the barn and not contained at the same time?
Figure 1.4.1 – Ladder & Barn Paradox
As with everything else in relativity, we can't trust our logic without converting everything into the language of spacetime events. In terms of events, what does it mean for the ladder to be “entirely within the barn?” Well, imagine that each end of the ladder is equipped with a flashbulb that flashes whenever it is in a doorway of the barn. We can say that the ladder is just barely “completely enclosed” if the light at the front of the ladder flashes in the exit doorway at the same instant that the light at the rear of the ladder flashes in the entrance doorway. Then we can say that both ends of the ladder are inside the barn at the same time. But we know from our discussion of simultaneity that what one observer sees as simultaneous events will not be seen as simultaneous by another. So the farmer sees the ladder as being within the barn because he can declare both ends to be within the confines of the barn at the same time, even as his wife claims that the front of the ladder exits the barn well in advance of the rear of the ladder entering it.
Figure 1.4.2 – Paradox Resolved By Discarding Simultaneity
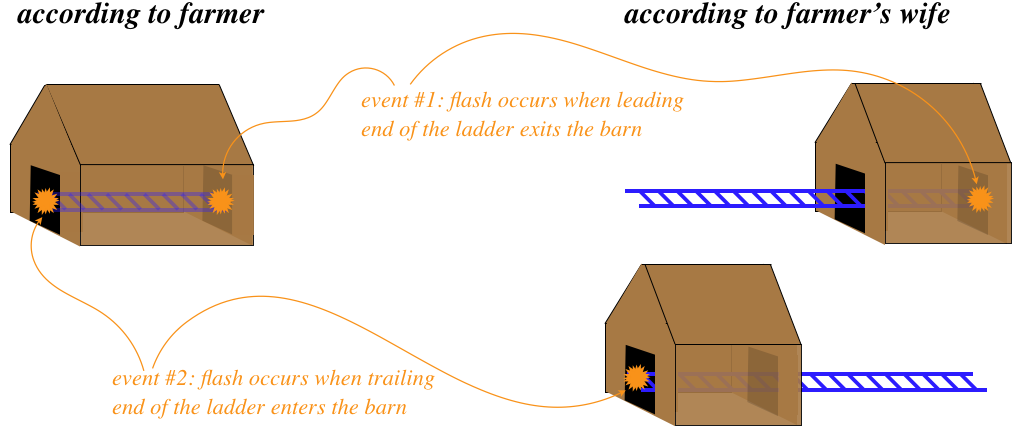
Once we accept that the idea of simultaneity is not universal, we realize that "being inside the barn" is a relative concept – two observers don't need to agree on this.
Okay, so much for the “dry run” of driving the ladder into one door and out the other. If the farmer can correctly claim that the ladder is within the barn, what happens if he closes the two barn doors simultaneously, while the ladder is in there? What will his wife see then?
If the barn door closings are simultaneous to the farmer, then they are not so for the wife. She would see the exiting barn door closed first, just as the front of the ladder gets there, and at that moment in her frame, the rear of the ladder will not be in the barn, and the entrance door is not yet being closed. But the question is, if the front of the ladder is stopped by the closed door, how does the rear of the ladder ever get in?
The answer to this is subtle and a bit beyond what we have discussed so far. Before we go into it, it is necessary to point out that everything we have been discussing to now points to a “cosmic speed limit” that is the speed of light. If two frames could move at the speed of light relative to each other, then one would witness time in the other frame to be stopped, and lengths to be shrunk to zero parallel to the direction of motion. This is an asymptotic speed limit that applies not only to solid objects, but also influences (such as forces and fields) and information.
Given that influences can’t travel faster than c, we must concede that even if we could somehow instantly stop the front of the ladder with the closed barn door, the rear of the ladder will keep moving forward until it “gets the message from the front” to stop. From the wife’s perspective, this means that the front of the barn will continue moving at v until the rear of the barn sends a message to it to stop moving. As time passes after the collision of the back door of the barn with the ladder, more and more of the barn will stop moving, until finally the front of the barn gets the message and the entire barn is at rest. If the message to stop could get to the front of the barn instantly, then of course the front door could never be closed and we would have a paradox, since the farmer clearly sees that it is possible to close both doors with the ladder within. So we need to calculate to see if the message is slow enough (even at the cosmic speed limit) to stop the front of the barn before the ladder can be enclosed.
Figure 1.4.3 – Can Both Barn Doors Be Closed?
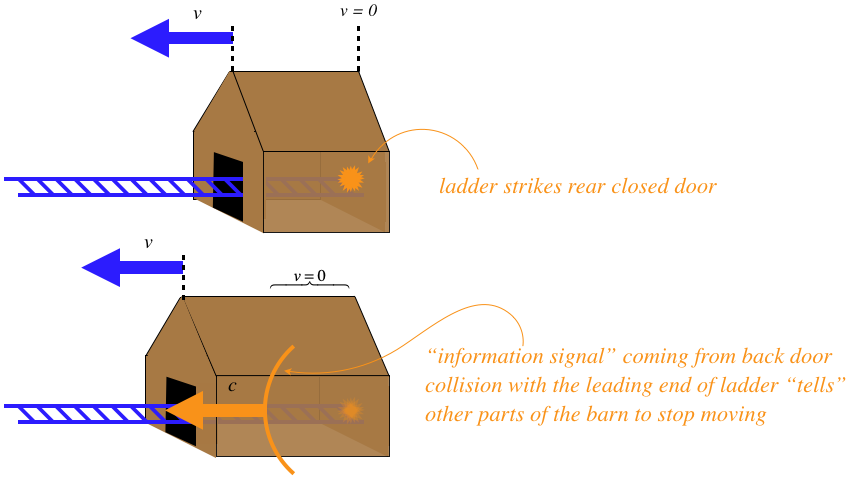
After t seconds in the wife's reference frame, the barn has gotten longer by an amount vΔt:
length of barn after t=32ft+vt=32ft+(0.6c)t
The distance that the light has traveled from the rear door in the wife's reference frame is equal to ct, so the signal reaches the front of the barn when:
ct=32ft+(0.6c)t⇒t=32ft0.4c
Okay, so we know how long it takes according to the wife for the barn to stop moving, so we can plug this time in to determine the maximum length of the barn:
length of stretched barn = distance the light travels in the total time =ct=32ft0.4=80ft
The ladder is 50ft long in the wife's frame, so it is inside the barn before the front of the barn gets the message to stop moving, and the barn door can be closed, averting the paradox entirely.
The Twin Paradox
The next paradox takes on time dilation. The idea is that if Ann and Bob can both see the other's clock ticking more slowly, what happens if, after awhile, we just bring both of the clocks together (into the same frame) and compare them? Which clock will have elapsed more time?
Two identical twins are born on a space station, and live there for their whole lives, until one of them gets into a spaceship for a long journey. When she speeds away from the space station at a sizable fraction of the speed of light, the twin on the space station (Ann) uses a powerful telescope to look through the window of her sister Bea’s spaceship, and sees the effects of time dilation as the clock on Bea’s ship is turning much slower than an identical clock in the space station. Bea also has a powerful telescope, and looking back at her sister, see that the space station clock is turning slow compared to her own. When Bea returns from her long journey and reunites with her sister, it would seem that both twins will encounter someone that is much younger than they are, but of course this is impossible. Which one will be older, or will they be the same age at the reunion?
The apparent paradox arises here because of symmetry. Each twin can claim that the other is moving because there is no such thing as a universal inertial frame. What is more, if we define the spacetime events as being the flash of light at the space dock that occurs during both the departure and the return, we see that both twins measure the proper time between these events, because the positions of both events in space are the same.
But is this symmetric? Both twins start in the same inertial frame, but in order to end up in different inertial frames, one of them has to change frames. For this to happen, she needs to accelerate, and this (at least while she is accelerating) puts her into a special non-inertial frame, which she can do an experiment to detect. The flash of light at the space dock occurs at the same position in each twin's frame, so they both measure a proper time, but only Ann measures the spacetime interval between those flashes, as only she stays in the inertial frame of the clock that records both events.
This means that the viewpoint of Ann remains correct – her sister experiences fewer years than she does during the trip. They started as twins, but after the trip Ann is several years older.
Alert
It is important to understand that this is not the fountain of youth – both twins age in the usual way. It isn't the rate of aging that is changed, it is the rate of time flow itself that is different. The older sister has more experiences than the younger one, and if they both live to be 100, they have equally-long lives. Their lives just don’t conclude at the same time, even though they started at the same time.
Let's do a specific calculation of this effect. Suppose that before the trip begins, Bea tells Ann that she’s going to a destination that is 20 light-years away and coming back. Her ship will travel at a more-or-less constant speed of 0.8c (except for the quick accelerations near the two endpoints). Ann does the simple math and determines that to cover the distance of the round trip at that speed will require 50 years:
Δx=vΔt⇒Δt=Δxv=40lightyears0.8c=50years
And this is in fact the amount of time that Ann measures for Bea’s trip. But what does Bea measure? Once Bea quickly gets up to speed, the distance isn't so far anymore, as the separation of the two endpoints is length-contracted (think of placing a very long rod between the endpoints). What is 20 light-years away in Ann's frame in Bea's frame is:
L′=20lightyearsγv=√1−(0.8cc)2(20lightyears)=12lightyears
At a speed of 0.8c, this 24 light-year round trip only takes 30 years. So Bea returns home to find that her twin sister is 20 years older than she is.
Let's call the departure of Bea and her arrival spacetime events A and B. Note that these both occur at the same place in space (Ann & Bea's home), which means that both Ann and Bea measure a proper time between the events. The fact that these are different comes back to our discussion around Equation 1.2.9 – the proper time measurement depends upon the history of the clock that measures it. Ann remains in an inertial frame, but Bea must accelerate to leave, turn around, and stop when arriving home. So the integrals come out different for the two sisters. This appeal to pure mathematics is perhaps not very satisfying, so let's try a new thought experiment to try to clear it up. This involves three players: Ann, Bob, and Chu, who have the following roles:
- Ann will be our “reference” observer. We will watch the motions of the other two through a telescope from the comfort of her (by her account, stationary) inertial frame on her spaceship.
- Bob will be engaging in a race from the starting point to the finish in a spaceship that travels in a straight line at a constant rate (as measured by Ann) of 0.5c. So Bob remains in an inertial frame throughout the trip.
- Chu will be the other contestant in the race, but he will get off to a slow start with a speed of 0.25c. Sometime during the race he will instantaneously speed his spaceship up to 0.75c (both speeds according to Ann) in an effort to catch up to Bob before the finish line.
All three participants have identical clocks on board their ships, and when the race begins, a flash of light (spacetime event) at the start line signifies the start of the race. When a ship crosses the finish line, another flash of light is given off there, providing a spacetime event that indicates that the ship has finished the race. Ann measures the distance between the start and finish lines as being 40 light-minutes (roughly the distance from our Sun to Jupiter).
Let's compute the time it takes Bob to complete the race, according to Ann. This is easy - no relativity necessary. Traveling at 0.5c over a distance of 40 light-minutes requires 80 minutes.
According to Ann, Chu makes his shift in speeds 40 minutes into the race (when Bob is halfway to the destination). So in the first 40 minutes at a speed of 0.25c, Chu travels 10 light-minutes. Then for the remaining 30 light-minutes of the trip he is traveling at 0.75c, which means it takes him 40 more minutes... He finishes in a tie with Bob!
The start and finish of the race both occur at the same position in Bob's frame (the front tip of his ship), and he is in an inertial frame, so he measures the proper time interval γ0.5cΔτBob=ΔtAnn, as we know from the time dilation formula between two inertial frames. Bob's time comes out to be:
ΔτBob=ΔtAnnγv=√32(80min)≈69min
Now let's compute the time measured by Chu. We can do this by splitting his trip into three events. We already have two of them – the flash that occurs at the start and finish. As with Bob, these two events occur at the same place in his frame, so he measures a proper time, but as his inertial frame changes, it is not the same. The third event we will define as a flash at the front tip of Chu's spaceship when he suddenly changes speeds. Now we can compute his time for each leg of the trip separately. He remains in an inertial frame during each leg, so we can use the time dilation of Ann for each leg (like we did for Bob's whole trip):
ΔτChu=ΔτChu(leg1)+ΔτChu(leg2)=ΔtAnn(leg1)γv1+ΔtAnn(leg2)γv2=√1−0.252(40min)+√1−0.752(40min)=√15+√74(40min)≈65min
So we see that less time elapses for Chu than for Bob during this race. So how does this apply to the twin paradox? Let's view the whole race from Bob's perspective. Let's call the direction of the race the +x-direction. According to Bob, he and Chu start at the same position, and Chu is initially going in the –x-direction (because Bob is moving faster than Chu in the +x direction according to Ann). A little while later, Bob sees Chu suddenly stop and immediately start coming back toward him (because Chu is now moving faster than Bob in the +x direction according to Ann), until they are back at the same position. Bob insists he was stationary the whole time, so according to Bob, Chu basically took off and came back. And sure enough, when he came mack, Chu had aged 4 minutes less than Bob.
While we haven't proven it with this one example, we do see a general result: For the same two spacetime events, all proper time measurements (like Bob's and Chu's) are shorter than all coordinate time measurements that are not proper (like Ann's). Also, the proper time interval between two events measured in an inertial frame (like Bob's) is longer than all of the other (non-inertial) proper time measurements (like Chu's).


