2.5: Energy Conservation
( \newcommand{\kernel}{\mathrm{null}\,}\)
One Last Thought Experiment
With an understanding of relativistic momentum conservation now firmly in hand, we will have a look at an inelastic collision. When we first encountered these in Physics 9HA, we said that no energy was actually "lost," it was just converted into another form (thermal). Given that thermal energy is at its core "microscopically mechanical," this assessment of it changing form is really just a shortcut, and in fact the only things that change in terms of energy is how it is packaged. For example, we could model a simple (perfectly) inelastic collision between two equal masses this way:
Figure 2.5.1 – A Simple Model of an Inelastic Collision

In this collision, if we can see what is going-on inside the boxed system after the collision, we can account for all of the incoming energy – part of it goes to the kinetic energy of the boxed system, and part of it to the potential and kinetic energy associated with the oscillation of the two particles. If we can't see what's going on, then we can only see the kinetic energy of the boxed system, and we call the leftover energy "internal energy" within the boxed system.
In Physics 9HA, for the non-relativistic case of a collision of this kind, we showed that the fraction of the initial kinetic energy the box system has after the collision is given by:
KEafterKEbefore=m1m1+m2=12
Put another way, for this case (non-relativistically, when the masses are equal), the energy contained in the oscillation of the two masses equals the kinetic energy of the box system after the collision.
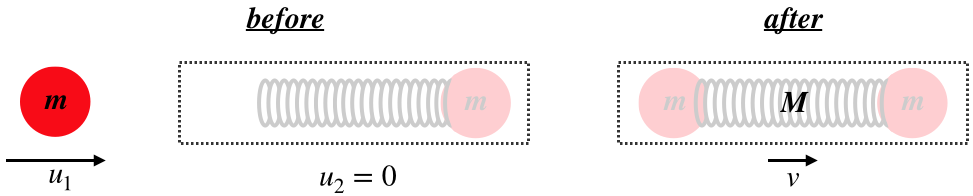
Let's see how all this works out for relativity with our new definition of momentum. We will watch this collision from two different perspectives. The first is Ann, who sees the collision from the perspective shown above, and who cannot see inside the boxed system, so she doesn't even know the system's mass after the collision (she calls it 'M'). Here is the before/after diagram she uses for momentum conservation:
Figure 2.5.2 – Ann's Before/After Diagram for a Perfectly Inelastic Collision
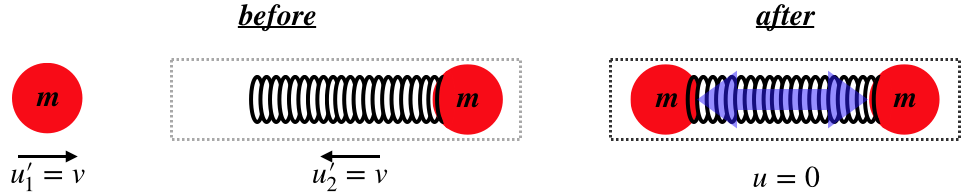
Bob will view the very same collision from another frame that is moving to the right with a speed of v, which is in the rest frame of the system after the collision. Unlike Ann, we'll say that he is able to see what is going on inside the box. With the two parts having equal mass, and coming to rest after the collision, he naturally must see both halves moving at the same speed, so from his perspective, the collision looks like this:
Figure 2.5.3 – Bob's Before/After Diagram for a Perfectly Inelastic Collision
Okay, so let's invoke relativistic momentum conservation for Ann. If she uses this to determine the unknown mass M, she finds:
Next all we have to do is relate u1 and v to each other using velocity addition:
u1=u′1+v1+u′1vc2=2v1+v2c2⇒u1v=2c2c2+v2
Writing γu1 in terms of v:
γu1=1√1−u21c2=1√1−(u1v⋅vc)2=1√1−(2c2c2+v2⋅vc)2=c2+v2√c4−2v2c2+v4=c2+v2c2−v2
Plugging everything back into Equation 2.5.2 reveals the mass that Ann measures for the combined system:
M=(c2+v2c2−v2γv)(2c2c2+v2)m=2γvm
Wait, Ann finds that the mass of the combined system is actually larger than 2m? This doesn't seem to agree with what Bob knows about the combined system. If the two masses were just held together, then Bob would be certain that the combined system would have a mass of 2m, but perhaps there is something about the fact that the masses are oscillating on the spring that adds to the mass of the system?
Perhaps we can get a clue about what is going on by looking at the mass discrepancy in the case of our familiar slow-moving world. The apparent additional mass is:
Δm=M−2m=M−Mγv=M(1−1γv)=M(1−√1−v2c2)
Now using the usual u<<c approximation:
√1−δ≈1−12δ⇒1−√1−v2c2≈1−(1−12v2c2)=12v2c2⇒Δm≈12Mv2c2
For this low-velocity case of two equal masses, we said above that the kinetic energy of the box system after the collision equals the internal energy contained in the oscillations, we therefore have:
internal energy=12Mv2=Δmc2
It appears that the energy that starts as kinetic and becomes internal due to an inelastic collision is manifested – according to relativity – as an increase in the mass of the system where the internal energy is contained, with a conversion factor of c2.
Total, Kinetic, and Rest Energy
What constitutes "internal energy" is determined by what we define as a system: Just aggregate a group of particles, and that group's collective mass is not simply the sum of the masses of the particles in the group, but must also include the mass that is equivalent to the energy of all their internal motion and interactions according to E=mc2. This famous equation is known as mass-energy equivalence, and it has interesting implications. For example, if we make an object hotter, then it contains more internal energy and therefore has more mass than when it is cooler.
In the example above, let's suppose Bob can't see inside the box. As we have said before, observers agree on masses, so he and Ann agree that the box has a mass of M. The box isn't moving in Bob's frame, so internal energy is the only energy the box has. The energy of a system measured in its rest frame is called the rest energy, and it comes from the system's total mass and mass-energy equivalence:
Erest=Mc2
If the energy of a system is instead measured in a frame in which it is not at rest, then there is a kinetic energy component that needs to be added to the rest energy to get the total energy. Naturally the total energy of a given system will be greater in frames in which the velocity of the system is greater. We can write the total energy as an unknown function of the velocity of the system in the frame, multiplied by the rest energy:
Etot=f(u)mc2
To obtain this function, let's look at the collision above from Bob's perspective. The energy is conserved, and at the end it is just the rest energy. Before the collision, the two particles have equal total energies whose sum is the final energy:
f(v)mc2+f(v)mc2=Mc2⇒f(v)=M2m⇒f(v)=γv
The final equality comes courtesy of Equation 2.5.5. So we conclude that the total energy of an object with mass m moving at a speed of u is given by:
Etot=γumc2
Example 2.5.1
Show that energy is conserved for the collision above when measured in Ann's frame.
- Solution
-
The total energy of the system before the collision comes in two pieces – the total energy of the incoming mass, and the rest energy of the target mass. After the collision the system's energy consists of the total energy of the moving total mass. We seek to show that these are equal:
γu1mc2+mc2?=γvMc2⇒γu1+1?=γvMm
Now substitute for Mm using Equation 2.5.5, giving:
γu1+1?=2γ2v
Now use Equation 2.5.4 to put everything in terms of v and c, and do the algebra:
c2+v2c2−v2+1=21−v2c2c2+v2+c2−v2c2−v2=2c2c2−v2
With the total energy and the rest energy of a system now in hand, it is easy to define the kinetic energy as the difference of the two:
KE=(γu−1)mc2
Example 2.5.2
Show that the relativistic kinetic energy is consistent with the non-relativistic definition of kinetic energy for speeds much less than c.
- Solution
-
Whenever we see the phrase "speeds much less than c," we immediately think of expanding γ to first order in v2c2, as we did in Equation 2.5.7:
KE=[γu−1]mc2=[(1−u2c2)−12−1]mc2≈[(1+12u2c2)−1]mc2=12mu2
Combining Energy and Momentum
Back in Physics 9HA, we found a very useful formula that relates kinetic energy to momentum. It's clear that the same formula does not work for relativity:
KE=(γu−1)mc2p22m=12m(γumu)2=12γ2umu2
This doesn't mean that there is no formula that relates these two quantities. Indeed:
E2=γ2um2c4=c2c2−u2m2c4=(u2c2−u2+1)m2c4=c2c2−u2m2u2c2+m2c4=γ2um2u2c2+m2c4=p2c2+m2c4
So the alternative ways of writing the total energy are:
E=γumc2=√p2c2+m2c4
Massless Particles
With the γu multiplying mc2 in the energy equation, we have another reason to insist that the speed of light is unobtainable – for a system to attain the speed of light, it would need to acquire infinite energy. But if this is true, does that mean that light has infinite energy? Of course not – we can measure the energy in light by absorbing it in matter and measuring the temperature change of the matter. So then how does light get away with moving at the cosmic speed limit? The answer is that while γu for light goes to infinity, the mass of a light "particle" (called a photon) turns out to be zero. The product of these two numbers turns out to result in a finite value.
Using the other energy equation tells us even more. Setting the mass equal to zero gives us a very simple relationship between the energy of a photon and its momentum:
So yes, light has both energy and momentum. Again, it might seem strange that something without mass can have momentum, but with γu exploding to infinity and the mass vanishing, this is again possible. The difference between light and matter in this regard is that photons don't have any rest energy – all of the energy comes from its momentum.


