4.8: Force-free Motion of a Rigid Symmetric Top
\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}
\newcommand{\id}{\mathrm{id}} \newcommand{\Span}{\mathrm{span}}
( \newcommand{\kernel}{\mathrm{null}\,}\) \newcommand{\range}{\mathrm{range}\,}
\newcommand{\RealPart}{\mathrm{Re}} \newcommand{\ImaginaryPart}{\mathrm{Im}}
\newcommand{\Argument}{\mathrm{Arg}} \newcommand{\norm}[1]{\| #1 \|}
\newcommand{\inner}[2]{\langle #1, #2 \rangle}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\kernel}{\mathrm{null}\,}
\newcommand{\range}{\mathrm{range}\,}
\newcommand{\RealPart}{\mathrm{Re}}
\newcommand{\ImaginaryPart}{\mathrm{Im}}
\newcommand{\Argument}{\mathrm{Arg}}
\newcommand{\norm}[1]{\| #1 \|}
\newcommand{\inner}[2]{\langle #1, #2 \rangle}
\newcommand{\Span}{\mathrm{span}} \newcommand{\AA}{\unicode[.8,0]{x212B}}
\newcommand{\vectorA}[1]{\vec{#1}} % arrow
\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow
\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vectorC}[1]{\textbf{#1}}
\newcommand{\vectorD}[1]{\overrightarrow{#1}}
\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}
\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}
\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}
\newcommand{\avec}{\mathbf a} \newcommand{\bvec}{\mathbf b} \newcommand{\cvec}{\mathbf c} \newcommand{\dvec}{\mathbf d} \newcommand{\dtil}{\widetilde{\mathbf d}} \newcommand{\evec}{\mathbf e} \newcommand{\fvec}{\mathbf f} \newcommand{\nvec}{\mathbf n} \newcommand{\pvec}{\mathbf p} \newcommand{\qvec}{\mathbf q} \newcommand{\svec}{\mathbf s} \newcommand{\tvec}{\mathbf t} \newcommand{\uvec}{\mathbf u} \newcommand{\vvec}{\mathbf v} \newcommand{\wvec}{\mathbf w} \newcommand{\xvec}{\mathbf x} \newcommand{\yvec}{\mathbf y} \newcommand{\zvec}{\mathbf z} \newcommand{\rvec}{\mathbf r} \newcommand{\mvec}{\mathbf m} \newcommand{\zerovec}{\mathbf 0} \newcommand{\onevec}{\mathbf 1} \newcommand{\real}{\mathbb R} \newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]} \newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]} \newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]} \newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]} \newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]} \newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]} \newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]} \newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]} \newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]} \newcommand{\laspan}[1]{\text{Span}\{#1\}} \newcommand{\bcal}{\cal B} \newcommand{\ccal}{\cal C} \newcommand{\scal}{\cal S} \newcommand{\wcal}{\cal W} \newcommand{\ecal}{\cal E} \newcommand{\coords}[2]{\left\{#1\right\}_{#2}} \newcommand{\gray}[1]{\color{gray}{#1}} \newcommand{\lgray}[1]{\color{lightgray}{#1}} \newcommand{\rank}{\operatorname{rank}} \newcommand{\row}{\text{Row}} \newcommand{\col}{\text{Col}} \renewcommand{\row}{\text{Row}} \newcommand{\nul}{\text{Nul}} \newcommand{\var}{\text{Var}} \newcommand{\corr}{\text{corr}} \newcommand{\len}[1]{\left|#1\right|} \newcommand{\bbar}{\overline{\bvec}} \newcommand{\bhat}{\widehat{\bvec}} \newcommand{\bperp}{\bvec^\perp} \newcommand{\xhat}{\widehat{\xvec}} \newcommand{\vhat}{\widehat{\vvec}} \newcommand{\uhat}{\widehat{\uvec}} \newcommand{\what}{\widehat{\wvec}} \newcommand{\Sighat}{\widehat{\Sigma}} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \definecolor{fillinmathshade}{gray}{0.9}Notation:
- I_{1}, I_{2}, I_{3} are the principal moments of inertia. I_{3} is the unique moment. If it is the largest of the three, the body is an oblate symmetric top; if it is the smallest, it is a prolate spherical top.
- Ox_{0}, Oy_{0}, Oz_{0} are the corresponding body-fixed principal axes.
- \omega_{1}, \omega_{2}, \omega_{3} are the components of the angular velocity vector \boldsymbol\omega with respect to the principal axes.
In the analysis that follows, we are going to have to think about three vectors. There will be the angular momentum vector \bf{L}, which, in the absence of external torques, is fixed in magnitude and in the direction in laboratory space. There will be the direction of the axis of symmetry, the Oz_0 axis, which is fixed in the body, but not necessarily in space, unless the body happens to be rotating about its axis of symmetry; we’ll denote a unit vector in this direction by \hat{\bf z}_{0} . And there will be the instantaneous angular velocity vector \omega which is neither space- nor body-fixed.
What we are going to find is the following. We shall find that \boldsymbol\omega precesses in the body about the body-fixed symmetry axis in a cone called the body cone. The angle between \boldsymbol\omega and \bf{\hat{z}_{0}} is constant (we’ll be calling this angle \alpha), and the magnitude \omega of \boldsymbol\omega of is constant. We shall find that the sense of the precession is the same as the sense of the spin if the body is oblate, but opposite if it is prolate. The direction of the symmetry axis, however, is not fixed in space, but it precesses about the space-fixed angular momentum vector \bf{L} in another cone. This cone is narrower than the body cone if the body is oblate, but broader than the body cone if the body is prolate. The net result of these two precessional motions is that precesses \omega in space about the space-fixed angular momentum vector in a cone called the space cone. For a prolate top, the semi vertical angle of the space cone can be anything from 0° to 90°; for an oblate top, however, the semi vertical angle of the space cone cannot exceed 19° 28' . That’s quite a lot to take in in one breath!
We can start with Euler’s equations of motion for force-free rotation of a symmetric top:
\begin{align} I_{1}\dot{\omega_{1}} &= -\omega_{2}\omega_{3}(I_{3}-I_{1}), \tag{4.8.1}\label{eq:4.8.1} \\[5pt] I_{1}\dot{\omega_{2}} &= -\omega_{1}\omega_{3}(I_{3}-I_{1}), \tag{4.8.2}\label{eq:4.8.2} \\[5pt] I_{3}\dot{\omega_{3}} &= 0. \tag{4.8.3}\label{eq:4.8.3} \end{align}
From the first of these we obtain the result
\ \omega_{3} = \text{constant} \tag{4.8.4}\label{eq:4.8.4}
For brevity, I am going to let
\dfrac{(I_{3}-I_{1})}{I_{1}} = \Omega , \tag{4.8.5}\label{eq:4.8.5}
although in a moment \Omega will have a physical meaning.
Equations \ref{eq:4.8.1} and \ref{eq:4.8.2} become:
\ \dot{\omega_{1}} = \Omega\omega_{2} \tag{4.8.6}\label{eq:4.8.6}
and
\ \dot{\omega_{2}} = \Omega\omega_{1} \tag{4.8.7}\label{eq:4.8.7}
Eliminate \omega_{2} from these to obtain
\ \dot{\omega_{1}} = - \Omega^{2}\omega_{1} \tag{4.8.8}\label{eq:4.8.8}
This is the Equation for simple harmonic motion and its solution is
\ \omega_{1} = \omega_{0} \cos (\Omega t + \epsilon) \tag{4.8.9}\label{eq:4.8.9}
in which \omega_{0} and \epsilon, the two constants of integration, whose values depend on the initial conditions in the usual fashion, are the amplitude and initial phase angle. On combining this with Equation \ref{eq:4.8.6}, we obtain
\ \omega_{2} = \omega_{0}\sin(\Omega t + \epsilon) \tag{4.8.10}\label{eq:4.8.10}
From these we see that (\omega_{1}^{2}+\omega_{2}^{2})^{1/2}, which is the magnitude of the component of \omega in the x_{0}y_{0}-plane, is constant, equal to \omega_{0}; and since \omega_{3} is also constant, it follows that (\omega_{1}^{2} + \omega_{2}^{2} + \omega_{3}^{2})^{1/2} , which is the magnitude of \omega, is also constant. The cosine of the angle \alpha between \hat{z_{0}} and \boldsymbol\omega is \omega_{3}/(\omega_{1}^{2} + \omega_{2}^{2} + \omega_{3}^{2})^{1/2} , and its sine is \omega_{0}/(\omega_{1}^{2} + \omega_{2}^{2} + \omega_{3}^{2})^{1/2} , so that \alpha is constant. Equations \ref{eq:4.8.9} and \ref{eq:4.8.10} tell us, then, that the vector \omega is precessing around the symmetry axis at an angular speed \Omega. Making use of Equation \ref{eq:4.8.5}, we find that
\cos \alpha = \dfrac{\omega_{3}}{\omega} = \dfrac{I_{1} \Omega}{(I_{3}-I_{1})\omega} \tag{4.8.11}\label{eq:4.8.11}
If we take the direction of the z_{0} axis to be the direction of the component of \omega along the symmetry axis, then \boldsymbol\Omega is in the same direction as {\bf z}_{0} if I_{3}>I_{1} (that is, if the top is oblate) and it is in the opposite direction if the top is prolate. The situation for oblate and prolate tops is shown in Figure IV.11.
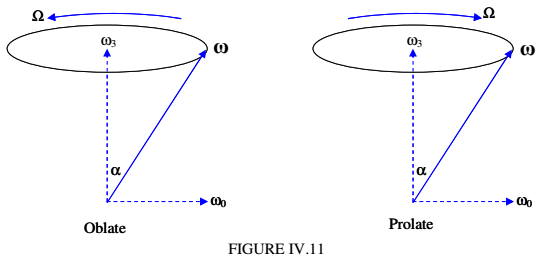
We have just dealt with how the instantaneous axis of rotation precesses about the body-fixed symmetry axis, describing the body cone of semi vertical angle \alpha .
Now we are going to consider the precession of the body-fixed symmetry axis about the space-fixed angular momentum vector \bf{L}. I am going to make use of the idea of Eulerian angles for expressing the orientation of one three-dimensional set of axes with respect to another. If you are not already familiar with Eulerian angles or would like a refresher, you can go to to Chapter 3 of Celestial Mechanics especially Section 3.7.
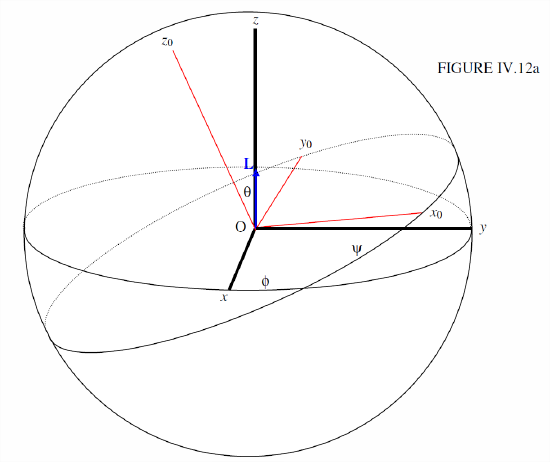
Recall that we are using Ox_{0}y_{0}z_{0} for body-fixed coordinates, referred to the principal axes. I shall use Oxyz for space-fixed coordinates, and there is no loss of generality if I choose the Oz axis to coincide with the angular momentum vector \bf{L}. Let me try to draw the situation in Figure IV.12a. The axes Oxyz are the space-fixed axes. The axes Ox_{0}y_{0}z_{0} are the body-fixed principal axes. The angular momentum vector \bf{L} is directed along the axis Oz. The symmetry axis of the body is directed along the axis Oz_{0}. The Eulerian angles of the body-fixed axes relative to the space fixed axes are ( \phi, \theta, \psi).
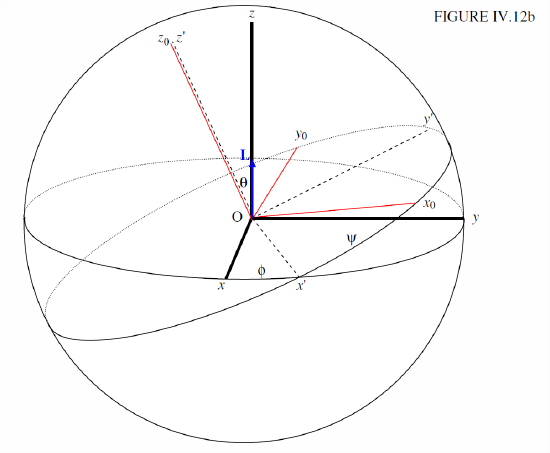
Recall, with the aid of Figure IV.12b, how these Euler angles are formed:
First, a rotation by \phi about Oz. Second, a rotation by \theta about the dashed line Ox^{\prime} to form an intermediate set of axes Ox^{\prime}y^{\prime}z^{\prime} . Third, a rotation by \psi about Oz^{\prime} to form the body- fixed principal axes Ox_{0}y_{0}z_{0}.
Spend a little time trying to visualize these three sets of axes. Please also convince yourself, from the way the Euler angles were formed through three rotations, that the vector \bf{L} is in the y_{\prime}z_{\prime} plane and has no x^{\prime} component. It is also in the y_{0}z_{0} plane and has no x_{0} component.
You will then agree that
\ L_{x'} = 0, \quad L_{y'} = L\sin \theta \quad L_{z'} = L\cos \theta . \tag{4.8.12}\label{eq:4.8.12}
Now if L_{x^{\prime}} = 0, then \omega_{x^{\prime}} is also zero, which means that \boldsymbol\omega, like \bf{L}, is in the y^{\prime}z^{\prime} plane.
We have seen that \boldsymbol\omega makes an angle \alpha with the symmetry axis Oz_{0}, where \alpha is given by Equation \ref{eq:4.8.11}.
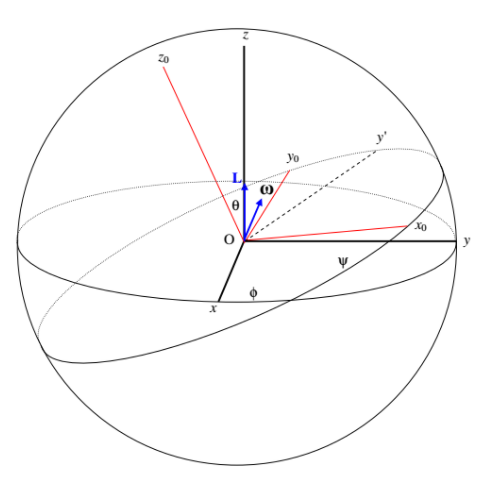
I’ll now add \boldsymbol\omega to the drawing to make Figure IV.13. Like \bf{L}, it is in the y'z' plane and has no x' component. I haven’t marked in the angle \alpha. I leave it to your imagination. It is the angle between \boldsymbol\omega and z_{0}. You should easily agree that
\ \omega_{x'} = 0, \quad \omega_{y'} + \omega \sin\alpha, \quad \omega_{z'} = \omega cos \alpha. \tag{4.8.13}\label{eq:4.8.13}
From these, together with L_{y'} = I_{1}\omega_{y'} and L_{z'} = I_{1}\omega_{z'} we obtain
\ I_{1} = \tan \alpha = I_{3} \tan \theta \tag{4.8.14}\label{eq:4.8.14}
- For an oblate symmetric top, I_{3}>I_{1}, \alpha>\theta.
- For a prolate symmetric top, I_{3}<I_{1}, \alpha<\theta.
Now \boldsymbol\omega can be written as the vector sum of the rates of change of the three Euler angles:
\boldsymbol\omega = \dot{\boldsymbol\theta} + \dot{\boldsymbol\phi} + \dot{\boldsymbol\psi} \tag{4.8.15}\label{eq:4.8.15}
The components of \dot{\boldsymbol\theta} and \dot{\boldsymbol\psi} along Oy^{\prime} are each zero, and therefore the component of \omega along Oy^{\prime} is equal to the component of \dot{\boldsymbol\psi} along Oy' .
\ \therefore \qquad \omega \sin\alpha = \dot{\phi}\sin{\theta} \tag{4.8.16}\label{eq:4.8.16}
In summary, then:
- The instantaneous axis of rotation, which makes an angle \alpha with the symmetry axis, precesses around it at angular speed \ \Omega = \dfrac{I_{3}-I_{1}}{I_{1}}\omega \cos \alpha \tag{4.8.17}\label{eq:4.8.17} which is in the same sense as \boldsymbol\omega if the top is oblate and opposite if it is prolate.
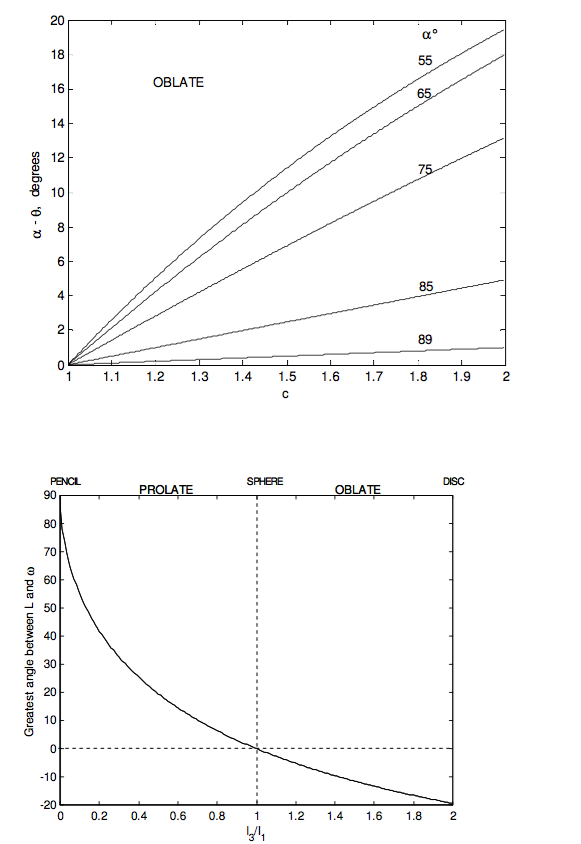
- The symmetry axis makes an angle \theta with the space-fixed angular momentum vector \bf{L}, where \ \tan \theta = \dfrac{I_{1}}{I_{3}}\tan \alpha. \tag{4.8.18}\label{eq:4.8.18} For an oblate top, \theta < \alpha. For a prolate top, \theta > \alpha.
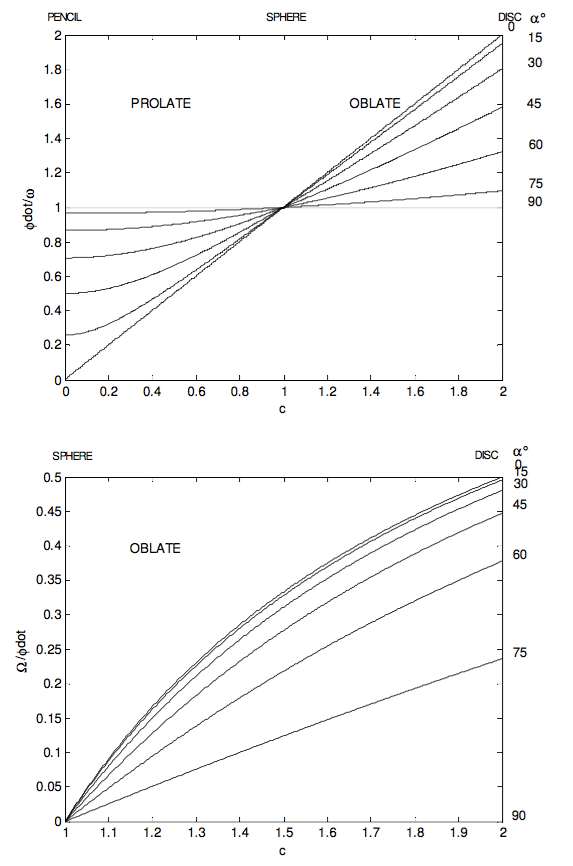
- The speed of precession of the symmetry axis about \bf{L} is \ \dot{\phi} = \dfrac{\sin \alpha}{\sin \theta} \omega, \tag{4.8.19}\label{eq:4.8.19} or, by elimination of \theta between \ref{eq:4.8.18} and \ref{eq:4.8.19}, \ \dot{\phi} = [ 1 +\dfrac{I_{3}^{2} - I_{1}^{2}}{I_{3}^{1}} \cos^{2} \alpha]^{1/2} \omega. \tag{4.8.20}\label{eq:4.8.20}
The net result of this is that \boldsymbol\omega preceses about \bf{L} at a rate \dot{\phi} in the space cone, which has a semi-vertical angle \alpha − \theta for an oblate rotator, and \theta − \alpha for a prolate rotator. The space cone is fixed in space, while the body cone rolls around it, always in contact, \boldsymbol\omega being a mutual generator of both cones. If the rotator is oblate, the space cone is smaller than the body cone and is inside it. If the rotator is prolate, the body cone is outside the space cone and can be larger or smaller than it.
Write
\ c = I_{3}/I_{1} \tag{4.8.21}\label{eq:4.8.21}
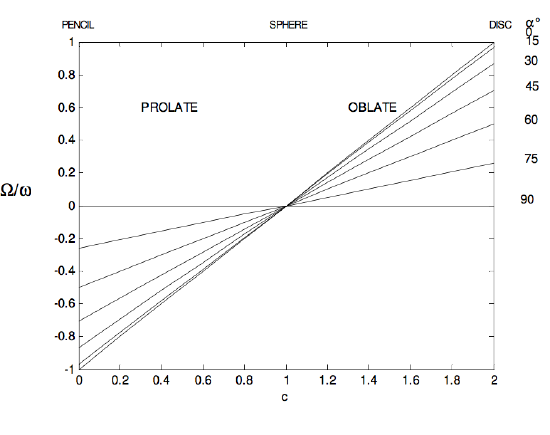
for the ratio of the principal moments of inertia. Note that for a pencil, c = 0; for a sphere, c = 1; for a plane disc or any regular plane lamina, c = 2. (The last of these follows from the perpendicular axes theorem.) The range of c, then, is from 0 to 2, 0 to 1 being prolate, 1 to 2 being oblate.
Equations \ref{eq:4.8.17} and \ref{eq:4.8.20} can be written
\ \dfrac{\Omega}{\omega} = (c-1)\cos\alpha \tag{4.8.22}\label{eq:4.8.22}
and
\ \dfrac{\dot{\phi}}{\omega} = [1 + (c^{2}-1)\cos^{2}\alpha]^{1/2} \tag{4.8.23}\label{eq:4.8.23}
Figures IV.15 and IV.16 show, for an oblate and a prolate rotator respectively, the instantaneouss rotation vector \boldsymbol\omega precessing around the body-fixed symmetry axis at a rate \Omega in the body cone of semi vertical angle \alpha; the symmetry axis precessing about the space-fixed angular momentum vector \bf{L} at a rate \dot{\phi} in a cone of semi vertical angle \theta (which is less than \alpha for an oblate rotator, and greater than \alpha for a prolate rotator; and consequently the instantaneous rotation vector \boldsymbol\omega precessing around the space-fixed angular momentum vector \bf{L} at a rate \dot{\phi} in the space cone of semi vertical angle \alpha − \theta (oblate rotator) or \theta − \alpha (prolate rotator).
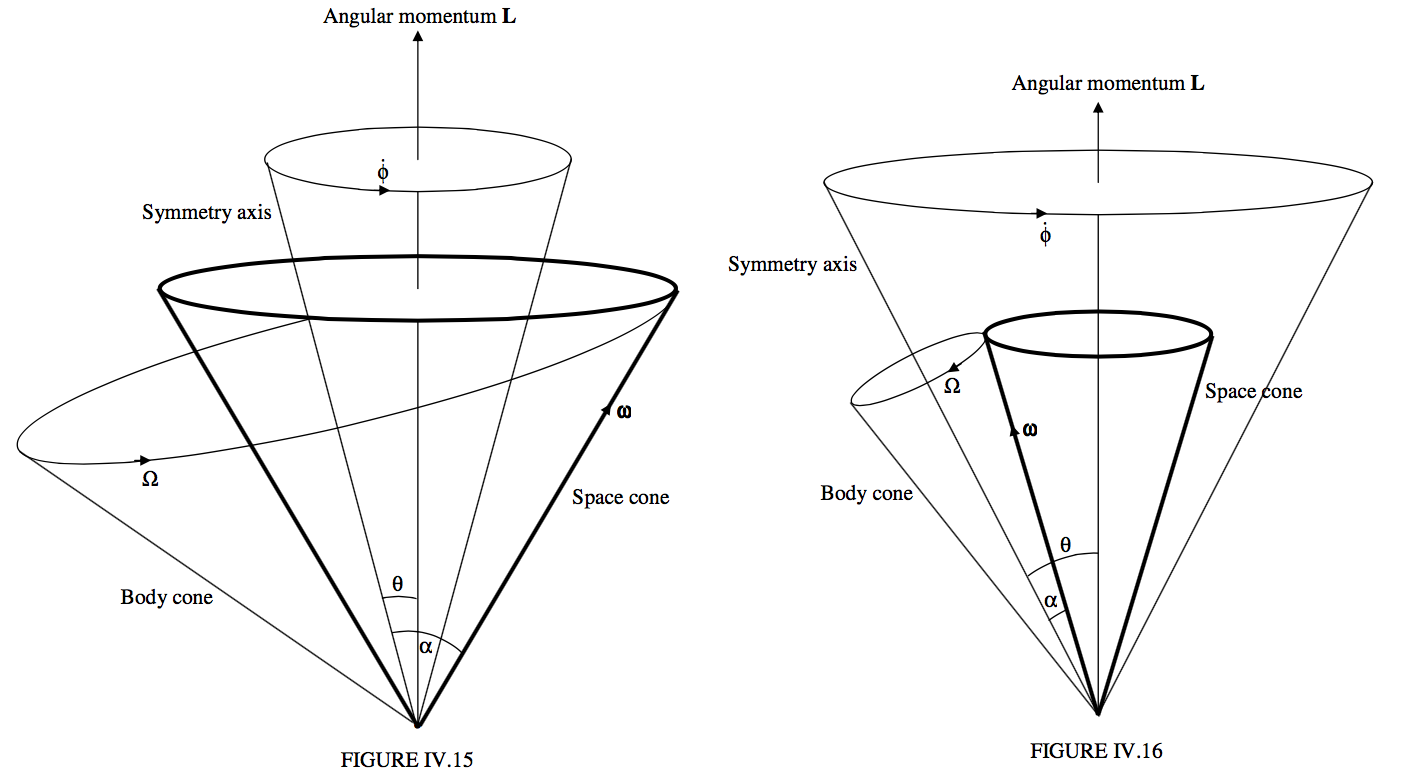
One can see from figures IV.15 and 16 that the angle between \bf{L} and \boldsymbol\omega is limited for an oblate rotator, but it can be as large as 90° for a prolate rotator. The angle between \bf{L} and \boldsymbol\omega is \theta − \alpha (which is negative for an oblate rotator). We have
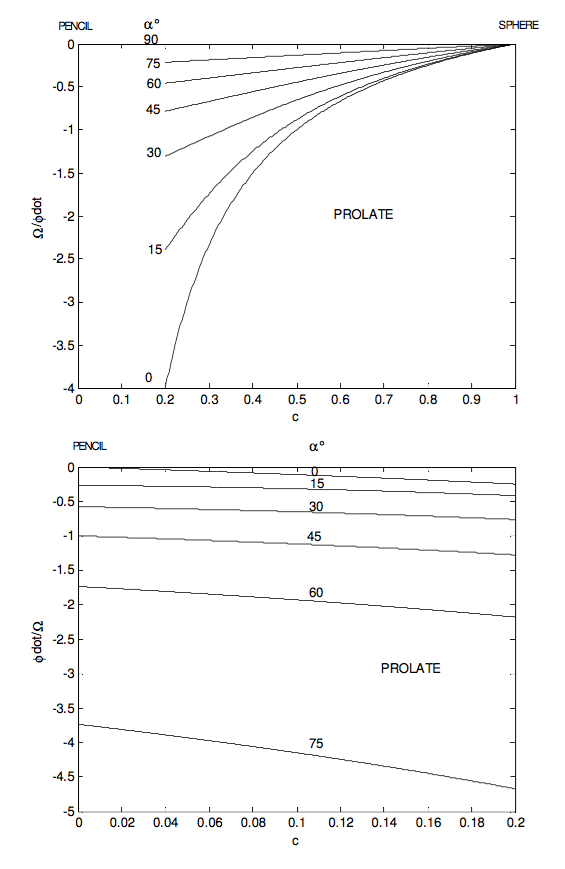
\ \tan (\theta - \alpha) = \dfrac{\tan\theta - \tan\alpha}{1 + \tan\theta \tan \alpha} = \dfrac{(1-c)\tan\alpha}{c+ \tan^{2}\alpha} \tag{4.8.24}\label{eq:4.8.24}
By calculus this reaches a maximum value of \dfrac{1-c}{2\sqrt{c}} for \tan \alpha = \sqrt{c}
For a rod or pencil (prolate), in which c = 0, the angle between \bf{L} and \boldsymbol\omega can be as large as 90°. Recalling exactly what are meant by the vectors \bf{L} and \boldsymbol\omega, the reader should try now and imagine in his or her mind’s eye a pencil rotating so that \bf{L} and \boldsymbol\omega are at right angles. The spin vector \boldsymbol\omega is along the length of the pencil and the angular momentum vector \bf{L} is at right angles to the length of the pencil.
For an oblate rotator, the angle between \bf{L} and \boldsymbol\omega is limited. The most oblate rotator is a flat disc or any regular flat lamina. The parallel axis theorem shows that for such a body, c=2. The greatest angle between \bf{L} and \boldsymbol\omega for a disc occurs when \tan \alpha =\sqrt{2} \alpha = 54° 44'),and then \tan \alpha− \theta = \dfrac{1}{\sqrt{8}}, \alpha - \theta =19° 28'.
In the following figures I illustrate some of these results graphically. The ratio \dfrac{I_{3}}{I_{1}} goes from 0 for a pencil through 1 for a sphere to 2 for a disc.
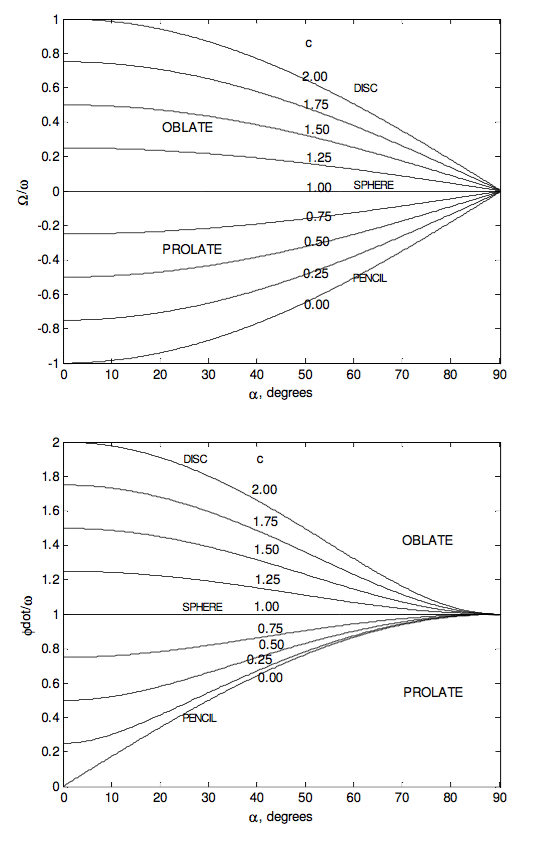
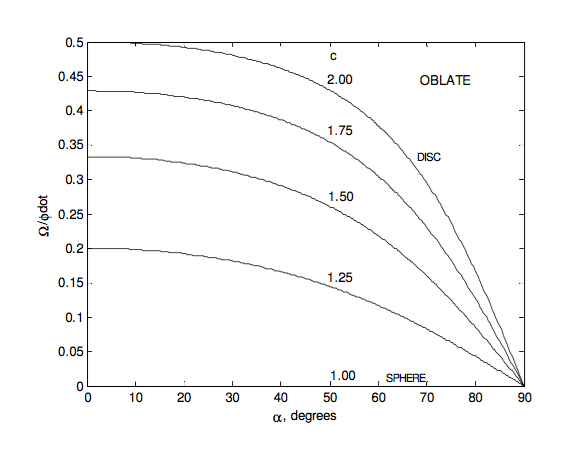
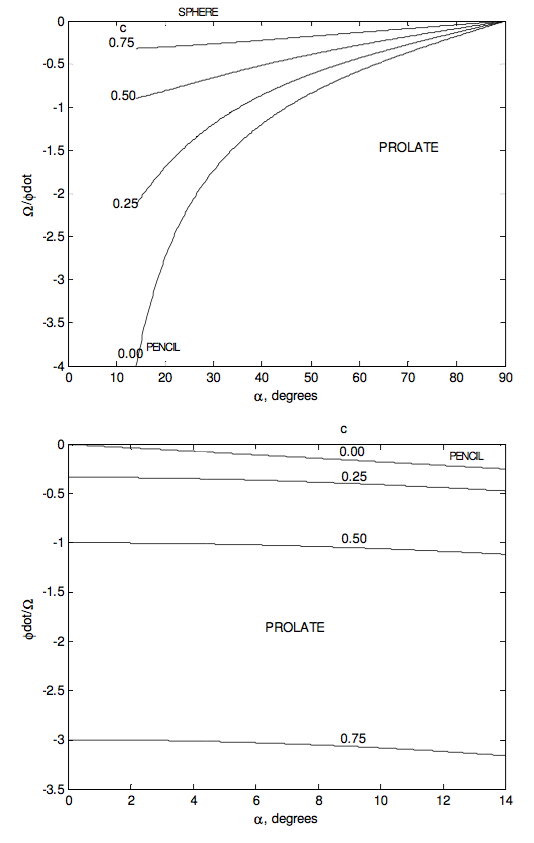
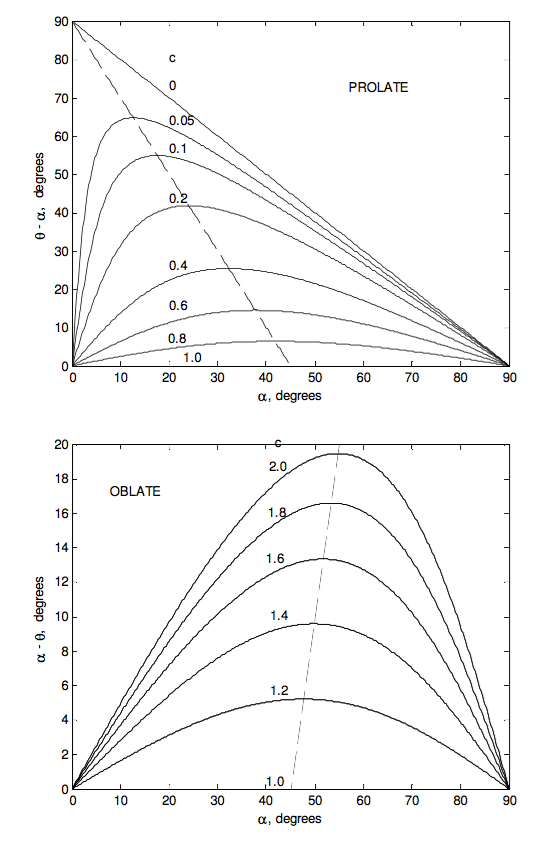
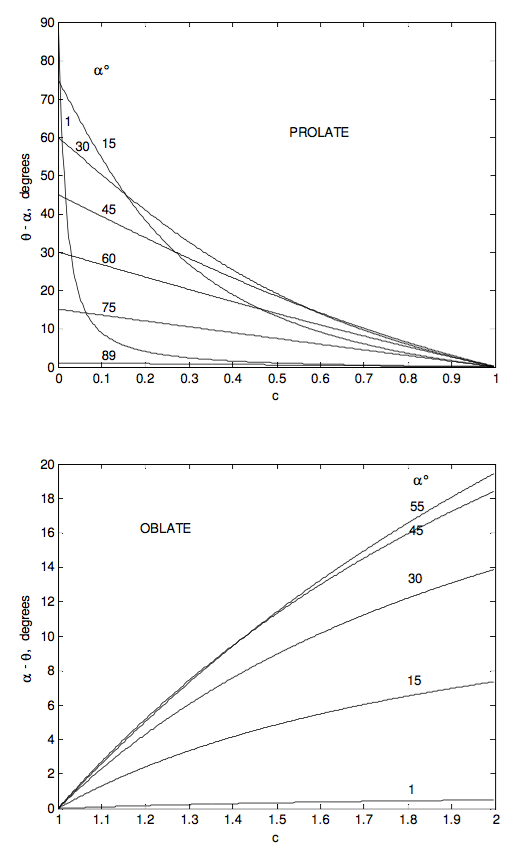
Our planet Earth is approximately an oblate spheroid, its dynamical ellipticity \dfrac{(I_{3}-I_{1})}{I_{1}} being about 3.285 × 10−3. It is not rotating exactly abut its symmetry axis; the angle \alpha between \boldsymbol\omega and the symmetry axis being about one fifth of an arcsecond, which is about six metres on the surface. The rotation period is one sidereal day (which is a few minutes shorter than 24 solar hours.) Equation \ref{eq:4.8.17} tells us that the spin axis precesses about the symmetry axis in a period of about 304 days, all within the area of a tennis court. The actual motion is a little more complicated than this. The period is closer to 432 days because of the nonrigidity of Earth, and superimposed on this is an annual component caused by the annual movement of air masses. This precessional motion of a symmetric body spinning freely about an axis inclined to the symmetry axis gives rise to variations of latitude of amplitude about a fifth of an arcsecond. It is not to be confused with the 26,000 year period of the precession of the equinoxes, which is caused by external torques from the Moon and the Sun.


