1.7: The Rainbow
\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}
\newcommand{\id}{\mathrm{id}} \newcommand{\Span}{\mathrm{span}}
( \newcommand{\kernel}{\mathrm{null}\,}\) \newcommand{\range}{\mathrm{range}\,}
\newcommand{\RealPart}{\mathrm{Re}} \newcommand{\ImaginaryPart}{\mathrm{Im}}
\newcommand{\Argument}{\mathrm{Arg}} \newcommand{\norm}[1]{\| #1 \|}
\newcommand{\inner}[2]{\langle #1, #2 \rangle}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\kernel}{\mathrm{null}\,}
\newcommand{\range}{\mathrm{range}\,}
\newcommand{\RealPart}{\mathrm{Re}}
\newcommand{\ImaginaryPart}{\mathrm{Im}}
\newcommand{\Argument}{\mathrm{Arg}}
\newcommand{\norm}[1]{\| #1 \|}
\newcommand{\inner}[2]{\langle #1, #2 \rangle}
\newcommand{\Span}{\mathrm{span}} \newcommand{\AA}{\unicode[.8,0]{x212B}}
\newcommand{\vectorA}[1]{\vec{#1}} % arrow
\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow
\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vectorC}[1]{\textbf{#1}}
\newcommand{\vectorD}[1]{\overrightarrow{#1}}
\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}
\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}
\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}
\newcommand{\avec}{\mathbf a} \newcommand{\bvec}{\mathbf b} \newcommand{\cvec}{\mathbf c} \newcommand{\dvec}{\mathbf d} \newcommand{\dtil}{\widetilde{\mathbf d}} \newcommand{\evec}{\mathbf e} \newcommand{\fvec}{\mathbf f} \newcommand{\nvec}{\mathbf n} \newcommand{\pvec}{\mathbf p} \newcommand{\qvec}{\mathbf q} \newcommand{\svec}{\mathbf s} \newcommand{\tvec}{\mathbf t} \newcommand{\uvec}{\mathbf u} \newcommand{\vvec}{\mathbf v} \newcommand{\wvec}{\mathbf w} \newcommand{\xvec}{\mathbf x} \newcommand{\yvec}{\mathbf y} \newcommand{\zvec}{\mathbf z} \newcommand{\rvec}{\mathbf r} \newcommand{\mvec}{\mathbf m} \newcommand{\zerovec}{\mathbf 0} \newcommand{\onevec}{\mathbf 1} \newcommand{\real}{\mathbb R} \newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]} \newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]} \newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]} \newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]} \newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]} \newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]} \newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]} \newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]} \newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]} \newcommand{\laspan}[1]{\text{Span}\{#1\}} \newcommand{\bcal}{\cal B} \newcommand{\ccal}{\cal C} \newcommand{\scal}{\cal S} \newcommand{\wcal}{\cal W} \newcommand{\ecal}{\cal E} \newcommand{\coords}[2]{\left\{#1\right\}_{#2}} \newcommand{\gray}[1]{\color{gray}{#1}} \newcommand{\lgray}[1]{\color{lightgray}{#1}} \newcommand{\rank}{\operatorname{rank}} \newcommand{\row}{\text{Row}} \newcommand{\col}{\text{Col}} \renewcommand{\row}{\text{Row}} \newcommand{\nul}{\text{Nul}} \newcommand{\var}{\text{Var}} \newcommand{\corr}{\text{corr}} \newcommand{\len}[1]{\left|#1\right|} \newcommand{\bbar}{\overline{\bvec}} \newcommand{\bhat}{\widehat{\bvec}} \newcommand{\bperp}{\bvec^\perp} \newcommand{\xhat}{\widehat{\xvec}} \newcommand{\vhat}{\widehat{\vvec}} \newcommand{\uhat}{\widehat{\uvec}} \newcommand{\what}{\widehat{\wvec}} \newcommand{\Sighat}{\widehat{\Sigma}} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \definecolor{fillinmathshade}{gray}{0.9}I do not know the exact shape of a raindrop, but I doubt very much if it is drop-shaped! Most raindrops will be more or less spherical, especially small drops, because of surface tension. If large, falling drops are distorted from an exact spherical shape, I imagine that they are more likely to be flattened to a sort of horizontal pancake shape rather than drop shaped. Regardless, in the analysis in this section, I shall assume drops are spherical, as I am sure small drops will be.
We wish to follow a light ray as it enters a spherical drop, is internally reflected, and finally emerges. See Figure I.15. We shall refer to the distance b as the impact parameter.
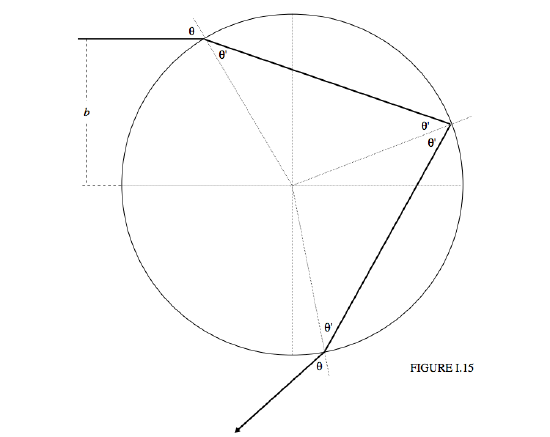
We see a ray of light headed for the drop, which I take to have unit radius, at impact parameter b. The deviation of the direction of the emergent ray from the direction of the incident ray is
D = \theta - \theta' + \pi -2\theta' +\theta - \theta' = \pi + 2\theta - 4\theta'. \label{eq:1.7.1}
However, we shall be more interested in the angle r = \pi − D. A ray of light that has been deviated by D will approach the observer from a direction that makes an angle r from the centre of the bow, which is at the anti-solar point (Figure I.16)
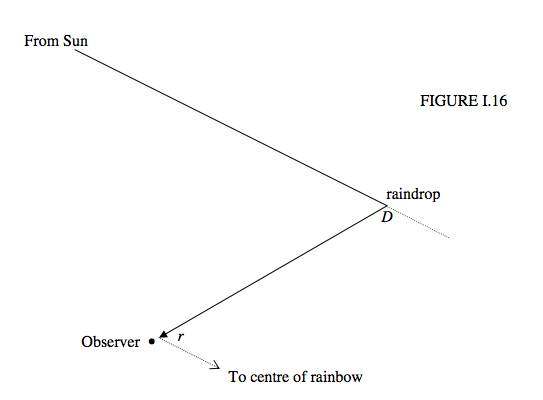
We would like to find the deviation D as a function of impact parameter. The angles of incidence and refraction are related to the impact parameter as follows:
\sin\theta=b,\label{eq:1.7.2}
\cos\theta=\sqrt{1-b^2},\label{eq:1.7.3}
\sin\theta' = b/n,\label{eq:1.7.4}
and
\cos\theta = \sqrt{1-b^2/n^2}. \label{eq:1.7.5}
These, together with Equation \ref{eq:1.7.1}, give us the deviation as a function of impact parameter. The deviation goes through a minimum – and r goes through a maximum. The deviation for a light ray of impact parameter b is
D = \pi + 2\sin^{-1}b - 4\sin^{-1}(b/n)\label{eq:1.7.6}
The angular distance r from the centre of the bow is r = \pi − D, so that
r = 4 \sin^{-1}(b/n) - 2\sin^{-1}b.\label{eq:1.7.7}
This is shown in Figure I.17 for n = 1.3439 (blue - \gamma = 400 nm) and n = 1.3316 (red - \gamma = 650 nm).
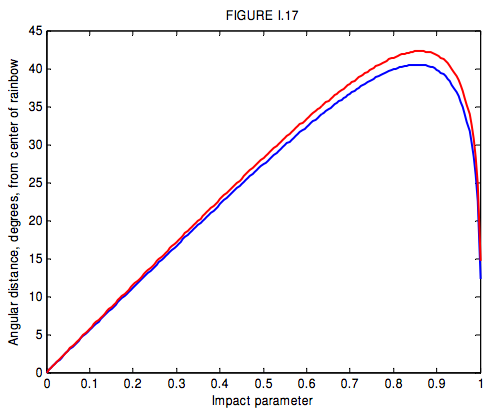
Differentiation gives the maximum value, R, of r - i.e. the radius of the bow – or the minimum deviation D_{\text{min}}. We obtain for the radius of the bow
R = 4\sin^{-1}\sqrt{\frac{4-n^2}{3n^2}}- 2\sin^{-1}\sqrt{\frac{4-n^2}{3}}. \label{eq:1.7.8}
For n = 1.3439 (blue) this is 40° 31' and for n = 1.3316 (red) this is 42° 17'. Thus the blue is on the inside of the bow, and red on the outside.
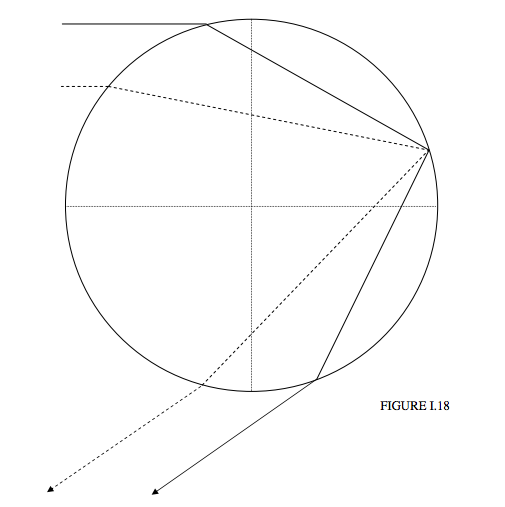
For grazing incidence (impact parameter = 1), the deviation is 2 \pi -4 \sin^{-1}(1/n), or 167° 40' for blue or 165° 18' for red. This corresponds to a distance from the centre of the bow r = 4 \sin^{-1}(1/n)-\pi, which is ' 12° 20' for blue and 14° 42' for red. It will be seen from figure I.17 that for radii less than R (i.e. inside the rainbow) but greater than 12° 20' for blue and 14° 42' for red there are two impact parameters that result in the same deviation, i.e. in the same position inside the bow. The paths of two rays with the same deviation are shown in Figure I.18. One ray is drawn as a full line, the other as a dashed line. They start with different impact parameters, and take different paths through the drop, but finish in the same direction. The drawing is done for a deviation of 145°, or 35° from the bow centre. The two impact parameters are 0.969 and 0.636. When these two rays are recombined by being brought to a focus on the retina of the eye, they have satisfied all the conditions for interference, and the result will be brightness or darkness according as to whether the path difference is an even or an odd number of half wavelengths.
If you look just inside the inner (blue) margin of the bow, you can often clearly see the interference fringes produced by two rays with the same deviation. I haven’t tried, but if you were to look through a filter that transmits just one colour, these fringes (if they are bright enough to see) should be well defined. The optical path difference for a given deviation, or given r, depends on the radius of the drop (and on its refractive index). For a drop of radius a it is easy to see that the optical path difference is
2a(\cos\theta_2 - \cos\theta_1) - 4n(\cos\theta'_2-\cos\theta'_1),
where \theta_1 is the larger of the two angles of incidence. Presumably, if you were to measure the fringe spacing, you could determine the size of the drops. Or, if you were to conduct a Fourier analysis of the visibility of the fringes, you could determine, at least in principle, the size distribution of the drops.
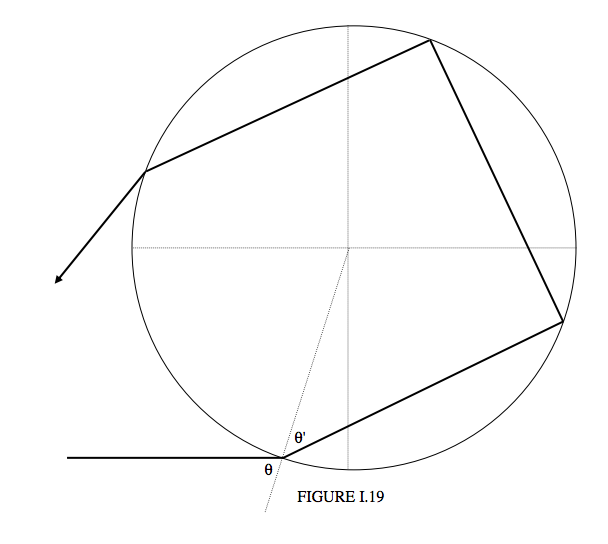
Some distance outside the primary rainbow, there is a secondary rainbow, with colours reversed – i.e. red on the inside, blue on the outside. This is formed by two internal reflections inside the drop (Figure I.19). The deviation of the final emergent ray from the direction of the incident ray is (\theta − \theta') + (π − 2\theta') + (π − 2\theta') + (\theta − \theta'), or 2π + 2\theta − 6\theta' counterclockwise, which amounts to D = 6\theta' − 2\theta clockwise. That is,
D = 6\sin^{-1}(b/n)-2\sin^{-1}b. \label{eq:1.7.9}
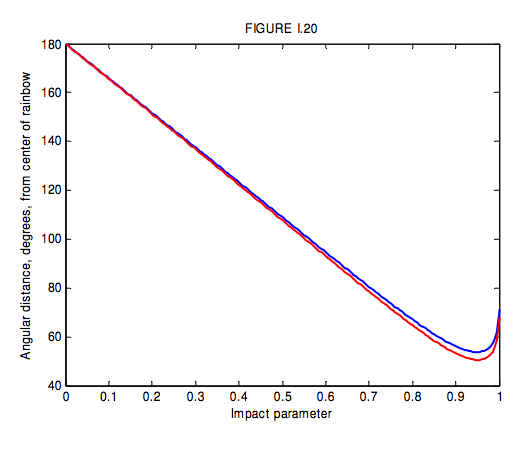
clockwise, and, as before, this corresponds to an angular distance from the centre of the bow r = \pi − D. I show in Figure I.20 the angular distance from the centre of the bow versus the impact parameter b. Notice that D goes through a maximum and hence r has a minimum value. There is no light scattered outside the primary bow, and no light scattered inside the secondary bow. When the full glory of a primary bow and a secondary bow is observed, it will be seen that the space between the two bows is relatively dark, whereas it is brighter inside the primary bow and outside the secondary bow.
Differentiation shows that the least value of r, (greatest deviation) corresponding to the radius of the secondary bow is
R = 6\sin^{-1} \sqrt{\frac{3-n^2}{2n^2}} - 2\sin^{-1}\sqrt{\frac{3-n^2}{2}}\label{eq:1.7.10}
For n = 1.3439 (blue) this is 53° 42' and for n = 1.3316 (red) this is 50° 31'. Thus the red is on the inside of the bow, and blue on the outside.
In principle a tertiary bow is possible, involving three internal reflections. I don’t know if anyone has observed a tertiary bow, but I am told that the primary bow is blue on the inside, the secondary bow is red on the inside, and “therefore” the tertiary bow would be blue on the inside. On the contrary, I assert that the tertiary bow would be red on the inside. Why is this?
Let us return to the primary bow. The deviation is (Equation \ref{eq:1.7.1}) D = π + 2\theta − 4\theta'. Let’s take n = 4/3, which it will be for somewhere in the middle of the spectrum. According to Equation \ref{eq:1.7.8}, the radius of the bow (R = \pi − D_{\text{min}}) is then about 42° . That is, 2\theta' − \theta = 21° . If we combine this with Snell’s law, 3\sin \theta = 4\sin \theta', we find that, at minimum deviation (i.e. where the primary bow is), \theta = 60°.5 and \theta' = 40°.8. Now, at the point of internal reflection, not all of the light is reflected (because \theta' is less than the critical angle of 36°.9), and it will be seen that the angle between the reflected and refracted rays is (180 − 60.6 − 40.8) degrees = 78°.6. Those readers who are familiar with Brewster’s law will understand that when the reflected and transmitted rays are at right angles to each other, the reflected ray is completely plane polarized. The angle, as we have seen, is not 90°, but is 78°.6, but this is sufficiently close to the Brewster condition that the reflected light, while not completely plane polarized, is strongly polarized. Thus, as can be verified with a polarizing filter, the rainbow is strongly plane polarized.
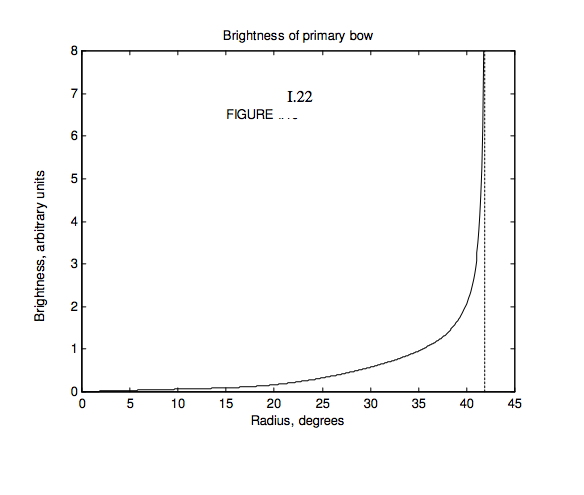
I now want to address the question as to how the brightness of the bow varies from centre to circumference. It is brightest where the slope of the deviation versus impact parameter curve is least – i.e. at minimum deviation (for the primary bow) or maximum deviation (for the secondary bow). Indeed the radiance (surface brightness) at a given distance from the centre of the bow is (among other things) inversely proportional to the slope of that curve. The situation is complicated a little in that, for deviations between D_{\text{min}} and 2\pi - 4\sin^{-1}(1/n), (this latter being the deviation for grazing incidence), there are two impact parameters giving rise to the same deviation, but for deviations greater than that (i.e. closer to the centre of the bow) only one impact parameter corresponds to a given deviation.
Let us ask ourselves, for example, how bright is the bow at 35° from the centre (deviation 145°)? The deviation is related to impact parameter by Equation \ref{eq:1.7.6}. For n = 4/3, we find that the impact parameters for deviations of 144, 145 and 146 degrees are as follows:
| D° | b |
|---|---|
| 144 | 0.6583 and 0.9623 |
| 145 | 0.6366 and 0.9693 |
| 146 | 0.6157 and 0.9736 |
Figure I.21 shows a raindrop seen from the direction of the approaching photons.
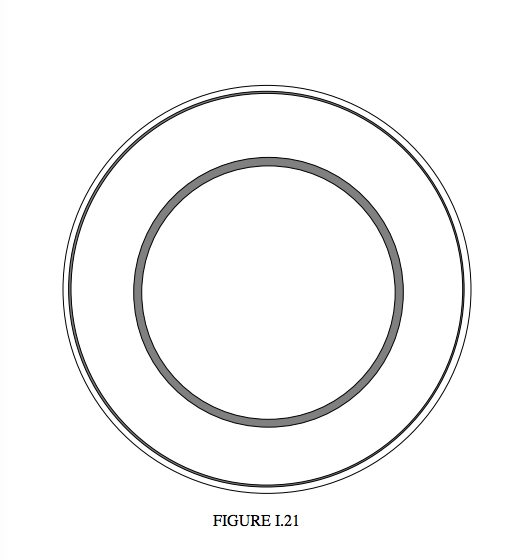
Any photons with impact parameters within the two dark annuli will be deviated between 144° and 146°, and will ultimately approach the observer at angular distances between 36° and 34° from the centre. The radiance at a distance of 35° from the centre will be proportional, among other things, to the sum of the areas of these two annuli.
I have said “among other things”. Let us now think about other things. I have drawn Figure I.15 as if all of the light is transmitted as it enters the drop, and then all of it is internally reflected within the drop, and finally all of it emerges when it leaves the drop. This is not so, of course. At entrance, at internal reflection and at emergence, some of the light is reflected and some is transmitted. The fractions that are reflected or transmitted depend on the angle of incidence, but, for minimum deviation, about 94% is transmitted on entry to and again at exit from the drop, but only about 6% is internally reflected. Also, after entry, internal reflection and exit, the percentage of polarization of the ray increases. The formulas for the reflection and transmission coefficients (Fresnel’s equations) are somewhat complicated (Equations 1.5.1 and 1.5.2) are for unpolarized incident light), but I have followed them through as a function of impact parameter, and have also taken account of the sizes of the one or two annuli involved for each impact parameter, and I have consequently calculated the variation of surface brightness for one color (n = 4/3) from the centre to the circumference of the bow. I omit the details of the calculations, since this chapter was originally planned as an elementary account of reflection and transmission, and we seem to have gone a little beyond that, but I show the results of the calculation in Figure I.22. I have not, however, taken account of the interference phenomena, which can often be clearly seen just within the primary bow.