4.2: Four-vectors (Part 1)
( \newcommand{\kernel}{\mathrm{null}\,}\)
The Velocity and Acceleration Four-vectors
Our basic Lorentz vector is the spacetime displacement dxi. Any other quantity that has the same behavior as dxi under rotations and boosts is also a valid Lorentz vector. Consider a particle moving through space, as described in a Lorentz frame. Since the particle may be subject to nongravitational forces, the Lorentz frame cannot be made to coincide (except perhaps momentarily) with the particle’s rest frame. If dxi is not lightlike, then the corresponding infinitesimal proper time interval dτ is nonzero. As with Newtonian three-vectors, dividing a four-vector by a Lorentz scalar produces another quantity that transforms as a four-vector, so dividing the infinitesimal displacement by a nonzero infinitesimal proper time interval, we have the four-velocity vector
vi=dxidτ
whose components in a Lorentz coordinate system are
(γ,γu1,γu2,γu3)
where (u1, u2, u3) is the ordinary three-component velocity vector as defined in classical mechanics. The four-velocity’s squared magnitude vivi is always exactly 1, even though the particle is not moving at the speed of light. (If it were moving at the speed of light, we would have dτ=0, and v would be undefined.)
When we hear something referred to as a “vector,” we usually take this is a statement that it not only transforms as a vector, but also that it adds as a vector. But we have already seen in Section 2.3 that even collinear velocities in relativity do not add linearly; therefore they clearly cannot add linearly when dressed in the clothing of four-vectors. We’ve also seen in Section 2.5 that the combination of non-collinear boosts is noncommutative, and is generally equivalent to a boost plus a spatial rotation; this is also not consistent with linear addition of four-vectors. At the risk of beating a dead horse, a four-velocity’s squared magnitude is always 1, and this is not consistent with being able to add four-velocity vectors.
Example 2: A zero velocity vector?
Suppose an object has a certain four-velocity vi in a certain frame of reference. Can we transform into a different frame in which the object is at rest, and its four-velocity is zero?
Solution
No. In general, the Lorentz transformation preserves the magnitude of vectors, so it can never transform a vector with a zero magnitude into one with nonzero magnitude. Since this is a material object (not a ray of light) we can transform into a frame in which the object is at rest, but an object at rest does not have a vanishing four-velocity. It has a four-velocity of (1, 0, 0, 0).
Example 2 suggests a nice way of thinking about velocity vectors, which is that every velocity vector represents a potential observer. An observer is a material object, and therefore has a timelike velocity vector. This observer writes her own velocity vector as (1, 0, 0, 0), i.e., as the unit vector in the timelike direction. Often when we see an expression involving a velocity vector, we can interpret it as describing a measurement taken by a specific observer.
Example 3: Orthogonality as simultaneity
In a space where the inner product can be negative, orthogonality doesn’t mean what our euclidean intuition thinks it means. For example, a lightlike vector can be orthogonal to itself — a situation that never occurs in a euclidean space. Suppose we have a timelike vector t and a spacelike one x. What would it mean for t and x to be orthogonal, with t · x = 0?
Solution
Since t is timelike, we can make a unit vector ˆt=t|t| out of it, and interpret ˆt as the velocity vector of some hypothetical observer. We then know that in that observer’s frame, ˆt is simply a unit vector along the time axis. It now becomes clear that x must be parallel to the x axis, i.e., it represents a displacement between two events that this observer considers to be simultaneous.
This is an example of the idea that expressions involving velocity vectors can be interpreted as measurements taken by a certain observer. The expression t · x = 0 can be interpreted as meaning that according to an observer whose world-line is tangent to t, x represents a relationship of simultaneity.
The four-acceleration is found by taking a second derivative with respect to proper time. Its squared magnitude is only approximately equal to minus the squared magnitude of the Newtonian acceleration three-vector, in the limit of small velocities.
Example 4: Constant acceleration
Suppose a spaceship moves so that the acceleration is judged to be the constant value a by an observer on board. Find the motion x(t) as measured by an observer in an inertial frame.
Solution
Let τ stand for the ship’s proper time, and let dots indicate derivatives with respect to τ. The ship’s velocity has magnitude 1, so $$\dot{t}^{2} - \dot{x}^{2} = 1 \ldotp\]
An observer who is instantaneously at rest with respect to the ship judges is to have a four-acceleration (0, a, 0, 0) (because the low-velocity limit applies). The observer in the (t, x) frame agrees on the magnitude of this vector, so
¨t2−¨x2=−a2.
The solution of these differential equations is t=1asinhaτ,x=1acoshaτ, and eliminating τ gives
x=1a√1+a2t2.
As t approaches infinity, dxdt approaches the speed of light.
The Momentum Four-vector
Definition for a Material Particle
If we hope to find something that plays the role of momentum in relativity, then the momentum three-vector probably needs to be generalized to some kind of four-vector. If so, then the law of conservation of momentum will be valid regardless of one’s frame of reference, which is necessary.2
Note
We are not guaranteed that this is the right way to proceed, since the converse is not true: some three-vectors such as the electric and magnetic fields are embedded in rank-2 tensors in more complicated ways than this. See section 4.2.
If we are to satisfy the correspondence principle then the relativistic definition of momentum should probably look as much as possible like the nonrelativistic one. Earlier, we defined the velocity four-vector in the case of a particle whose dxi is not lightlike. Let’s assume for the moment that it makes sense to think of mass as a scalar. As with Newtonian three-vectors, multiplying a Lorentz scalar by a four-vector vector produces another quantity that transforms as a four-vector. We therefore conjecture that the four-momentum of a material particle can be defined as pi = mvi, which in Lorentz coordinates is (mγ,mγv1,mγv2,mγv3). There is no a priori guarantee that this is right, but it’s the most reasonable thing to guess. It needs to be checked against experiment, and also for consistency with the other parts of our theory.
The spacelike components look like the classical momentum vector multiplied by a factor of γ, the interpretation being that to an observer in this frame, the moving particle’s inertia is increased relative to its value in the particle’s rest frame. Such an effect is indeed observed experimentally. This is why particle accelerators are so big and expensive. As the particle approaches the speed of light, γ diverges, so greater and greater forces are needed in order to produce the same acceleration. In relativistic scattering processes with material particles, we find empirically that the four-momentum we’ve defined is conserved, which confirms that our conjectures above are valid, and in particular that the quantity we’re calling m can be treated as a Lorentz scalar, and this is what all physicists do today. The reader is cautioned, however, that up until about 1950, it was common to use the word “mass” for the combination mγ (which is what occurs in the Lorentz-coordinate form of the momentum vector), while referring to m as the “rest mass.” This archaic terminology is only used today in some popular-level books and low-level school textbooks.
Equivalence of Mass and Energy
The momentum four-vector has locked within it the reason for Einstein’s famous E = mc2, which in our relativistic units becomes simply E = m. To see why, consider the experimentally measured inertia of a physical object made out of atoms. The subatomic particles are all moving, and many of the velocities, e.g., the velocities of the electrons, are quite relativistic. This has the effect of increasing the experimentally determined inertial mass of the whole object, by a factor of γ averaged over all the particles — even though the masses of the individual particles are invariant Lorentz scalars. (This same increase must also be observed for the gravitational mass, based on the equivalence principle as verified by Eötvös experiments.)
Now if the object is heated, the velocities will increase on the average, resulting in a further increase in its mass. Thus, a certain amount of heat energy is equivalent to a certain amount of mass. But if heat energy contributes to mass, then the same must be true for other forms of energy. For example, suppose that heating leads to a chemical reaction, which converts some heat into electromagnetic binding energy. If one joule of binding energy did not convert to the same amount of mass as one joule of heat, then this would allow the object to spontaneously change its own mass, and then by conservation of momentum it would have to spontaneously change its own velocity, which would clearly violate the principle of relativity. We conclude that mass and energy are equivalent, both inertially and gravitationally. In relativity, neither is separately conserved; the conserved quantity is their sum, referred to as the mass-energy, E. An alternative derivation, by Einstein, is given in example 16.
Energy is the Timelike Component of the Four-momentum
The Lorentz transformation of a zero vector is always zero. This means that the momentum four-vector of a material object can’t equal zero in the object’s rest frame, since then it would be zero in all other frames as well. So for an object of mass m, let its momentum four-vector in its rest frame be (f(m), 0, 0, 0), where f is some function that we need to determine, and f can depend only on m since there is no other property of the object that can be dynamically relevant here. Since conservation laws are additive, f has to be f(m) = km for some universal constant k. In where c = 1, k is unitless. Since we want to recover the appropriate Newtonian limit for massive bodies, and since vt = 1 in that limit, we need k = 1. Transforming the momentum four-vector from the particle’s rest frame into some other frame, we find that the timelike component is no longer m. We interpret this as the relativistic mass-energy, E.
Since the momentum four-vector was obtained from the magnitude-1 velocity four-vector through multiplication by m, its squared magnitude pipi is equal to the square of the particle’s mass. Writing p for the magnitude of the momentum three-vector, and E for the mass-energy, we find the useful relation m2 = E2 −p2. We take this to be the relativistic definition the mass of any particle, including one whose dxi is lightlike.
Particles Traveling at c
The definition of four-momentum as pi = mvi only works for particles that move at less than c. For those that move at c, the four-velocity is undefined. As we’ll see in example 6, this class of particles is exactly those that are massless. As shown in section 1.5, the three-momentum of a light wave is given by p = E. The fact that this momentum is nonzero implies that for light pi = mvi represents an indeterminate form. The fact that this momentum equals E is consistent with our definition of mass as m2 = E2 − p2.
Mass is Not Additive
Since the momentum four-vector pa is additive, and our definition of mass as papa depends on the vector in a nonlinear way, it follows that mass is not additive (even for particles that are not interacting but are simply considered collectively).
Example 5: Mass of two light waves
Let the momentum of a certain light wave be (pt, px) = (E, E), and let another such wave have momentum (E, −E). The total momentum is (2E, 0). Thus this pair of massless particles has a collective mass of 2E.
Example 6: Massless particles travel at c
We demonstrate this by showing that if we suppose the opposite, then there are two different consequences, either of which would be physically unacceptable.
When a particle does have a nonvanishing mass, we have
limEm→∞|v|=limEm→∞|p|E=1.
Thus if we had a massless particle with |v| ≠ 1, its behavior would be different from the limiting behavior of massive particles. But this is physically unacceptable because then we would have a magic method for detecting arbitrarily small masses such as 10−10000000000 kg. We don’t actually know that the photon, for example, is exactly massless; see example 13.
Furthermore, suppose that a massless particle had |v| < 1 in the frame of some observer. Then some other observer could be at rest relative to the particle. In such a frame, the particle’s three-momentum p is zero by symmetry, since there is no preferred direction for it. Then E2 = p2 + m2 is zero as well, so the particle’s entire energy-momentum four-vector is zero. But a four-vector that vanishes in one frame also vanishes in every other frame. That means we’re talking about a particle that can’t undergo scattering, emission, or absorption, and is therefore undetectable by any experiment. This is physically unacceptable because we don’t consider phenomena (e.g., invisible fairies) to be of physical interest if they are undetectable even in principle.
Example 7: Gravitational redshifts
Since a photon’s energy E is equivalent to a certain gravitational mass m, photons that rise or fall in a gravitational field must lose or gain energy, and this should be observed as a redshift or blueshift in the frequency. We expect the change in gravitational potential energy to be EΔϕ, giving a corresponding opposite change in the photon’s energy, so that ΔEE=Δφ. In metric units, this becomes ΔEE=Δφc2, and in the field near the Earth’s surface we have ΔEE=ghc2. This is the same result that was found in section 1.5 based only on the equivalence principle, and verified experimentally by Pound and Rebka as described in section 1.5.
Example 8: Constraints on polarization
We observe that electromagnetic waves are always polarized transversely, never longitudinally. Such a constraint can only apply to a wave that propagates at c. If it applied to a wave that propagated at less than c, we could move into a frame of reference in which the wave was at rest. In this frame, all directions in space would be equivalent, and there would be no way to decide which directions of polarization should be permitted. For a wave that propagates at c, there is no frame in which the wave is at rest (see section 3.4).
Example 9: Relativistic work-energy theorem
In Einstein’s original 1905 paper on relativity, he assumed without providing any justification that the Newtonian work-energy relation W = Fd was valid relativistically. One way of justifying this is that we can construct a simple machine with a mechanical advantage A and a reduction of motion by 1A, with these ratios being exact relativistically.3 One can then calculate, as Einstein did,
W=∫dpdtdx=∫dpdvdxdtdv=m(γ−1),
which is consistent with our result for E as a function of γ if we equate it to E(γ) − E(1).
3 For an explicit example, see bit.ly/1aUXIa8.
Example 10: The Dirac sea
A great deal of physics can be derived from the T.H. White’s principle that “whatever is not forbidden in compulsory” — originally intended for ants but applied to particles by Gell-Mann. In quantum mechanics, any process that is not forbidden by a conservation law is supposed to occur. The relativistic relation E=±√p2+m2 has two roots, a positive one and a negative one. The positive-energy and negative-energy states are separated by a no-man’s land of width 2m, so no continuous classical process can lead from one side to the other. But quantum-mechanically, if an electron exists with energy E=+√p2+m2, it should be able to make a quantum leap into a state with E=−√p2+m2, emitting the energy difference of 2E in the form of photons. Why doesn’t this happen? One explanation is that the states with E < 0 are all already occupied. This is the “Dirac sea,” which we now interpret as being full of electrons. A vacancy in the sea manifests itself as an antielectron.
Example 11: Massive neutrinos
Neutrinos were long thought to be massless, but are now believed to have masses in the eV range. If they had been massless, they would always have had to propagate at the speed of light. Although they are now thought to have mass, that mass is six orders of magnitude less than the MeV energy scale of the nuclear reactions in which they are produced, so all neutrinos observed in experiments are moving at velocities very close to the speed of light.
Example 12: No radioactive decay of massless particles
A photon cannot decay into an electron and a positron, γ → e+ + e−, in the absence of a charged particle to interact with. To see this, consider the process in the frame of reference in which the electron-positron pair has zero total momentum. In this frame, the photon must have had zero (three-)momentum, but a photon with zero momentum must have zero energy as well. This means that conservation of relativistic four-momentum has been violated: the timelike component of the four-momentum is the mass-energy, and it has increased from 0 in the initial state to at least 2mc2 in the final state.
To demonstrate the consistency of the theory, we can arrive at the same conclusion by a different method. Whenever a particle has a small mass (small compared to its energy, say), it must travel at close to c. It must therefore have a very large time dilation, and will take a very long time to undergo radioactive decay. In the limit as the mass approaches zero, the time required for the decay approaches infinity. Another way of saying this is that the rate of radioactive decay must be fixed in terms of proper time, but there is no such thing as proper time for a massless particle. Thus it is not only this specific process that is forbidden, but any radioactive decay process involving a massless particle.
There are various loopholes in this argument. The question is investigated more thoroughly by Fiore and Modanese.4
Example 13: Massive photons
Continuing in the same vein as example 11, we can consider the possibility that the photon has some nonvanishing mass. A 2003 experiment by Luo et al.5 has placed a limit of about 10−54 kg on this mass. This is incredibly small, but suppose that future experimental work using improved techniques shows that the mass is less than this, but actually nonzero. A naive reaction to this scenario is that it would shake relativity to its core, since relativity is based upon the assumption that the speed of light is a constant, whereas for a massive particle it need not be constant. But this is a misinterpretation of the role of c in relativity. As should be clear from the approach taken in section 2.2, c is primarily a geometrical property of spacetime, not a property of light.
In reality, such a discovery would be more of a problem for particle physicists than for relativists, as we can see by the following sketch of an argument. Imagine two charged particles, at rest, interacting via an electrical attraction. Quantum mechanics describes this as an exchange of photons. Since the particles are at rest, there is no source of energy, so where do we get the energy to make the photons? The Heisenberg uncertainty principle, ΔEΔt≳, allows us to steal this energy, provided that we give it back within a time \Deltat. This time limit imposes a limit on the distance the photons can travel, but by using photons of low enough energy, we can make this distance limit as large as we like, and there is therefore no limit on the range of the force. But suppose that the photon has a mass. Then there is a minimum mass-energy mc2 required in order to create a photon, the maximum time is h/mc2, and the maximum range is h/mc. Refining these crude arguments a little, one finds that exchange of zeromass particles gives a force that goes like \frac{1}{r^{2}}, while a nonzero mass results in \frac{e^{− \mu r}}{r^{2}}, where \mu^{−1} = \frac{\hbar}{mc}. For the photon, the best current mass limit corresponds to \mu^{−1} \gtrsim 10^{11} m, so the deviation from \frac{1}{r^{2}} would be difficult to measure in earthbound experiments.
Now Gauss’s law is a specific characteristic of \frac{1}{r^{2}} fields. It would be violated slightly if photons had mass. We would have to modify Maxwell’s equations, and it turns out6 that the necessary change to Gauss’s law would be of the form \nabla \cdot \textbf{E} = (\ldots) \rho − (\ldots) \mu^{2} \Phi, where \Phi is the electrical potential, and (. . . ) indicates factors that depend on the choice of units. This tells us that \Phi, which in classical electromagnetism can only be measured in terms of differences between different points in space, can now be measured in absolute terms. Gauge symmetry has been broken. But gauge symmetry is indispensible in creating well-behaved relativistic field theories, and this is the reason that, in general, particle physicists have a hard time with forces arising from the exchange of massive particles. The hypothetical Higgs particle, which may be observed at the Large Hadron Collider in the near future, is essentially a mechanism for wriggling out of this difficulty in the case of the massive W and Z particles that are responsible for the weak nuclear force; the mechanism cannot, however, be extended to allow a massive photon.
5 Luo et al., “New Experimental Limit on the Photon Rest Mass with a Rotating Torsion Balance,” Phys. Rev. Lett. 90 (2003) 081801. The interpretation of such experiments is difficult, and this paper attracted a series of comments. A weaker but more universally accepted bound is 8 × 10−52 kg, Davis, Goldhaber, and Nieto, Phys. Rev. Lett. 35 (1975) 1402.
6 Goldhaber and Nieto, ”Terrestrial and Extraterrestrial Limits on The Photon Mass,” Rev. Mod. Phys. 43 (1971) 277
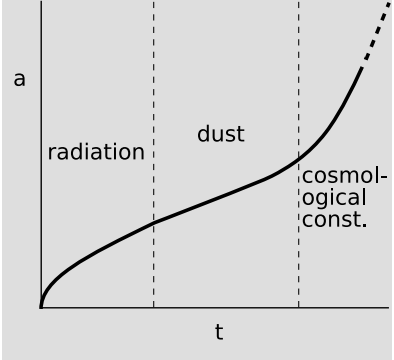
Example 14: Dust and radiation in cosmological models
In cosmological models, one needs an equation of state that relates the pressure P to the mass-energy density \rho. The pressure is a Lorentz scalar. The mass-energy density is not (since massenergy is just the timelike component of a particular vector), but in a coordinate system without any net flow of mass, we can approximate it as one.
The early universe was dominated by radiation. A photon in a box contributes a pressure on each wall that is proportional to |p\mu|, where \mu is a spacelike index. In thermal equilibrium, each of these three degrees of freedom carries an equal amount of energy, and since momentum and energy are equal for a massless particle, the average momentum along each axis is equal to \frac{1}{3} E. The resulting equation of state is P = \frac{1}{3} \rho. As the universe expanded, the wavelengths of the photons expanded in proportion to the stretching of the space they occupied, resulting in \lambda \propto a^{−1}, where a is a distance scale describing the universe’s intrinsic curvature at a fixed time. Since the number density of photons is diluted in proportion to a−3, and the mass per photon varies as a−1, both \rho and P vary as a−4.
Cosmologists refer to noninteracting, nonrelativistic materials as “dust,” which could mean many things, including hydrogen gas, actual dust, stars, galaxies, and some forms of dark matter. For dust, the momentum is negligible compared to the mass-energy, so the equation of state is P = 0, regardless of \rho. The massenergy density is dominated simply by the mass of the dust, so there is no red-shift scaling of the a−1 type. The mass-energy density scales as a−3. Since this is a less steep dependence on a than the a−4, there was a point, about a thousand years after the Big Bang, when matter began to dominate over radiation. At this point, the rate of expansion of the universe made a transition to a qualitatively different behavior resulting from the change in the equation of state.
In the present era, the universe’s equation of state is dominated by neither dust nor radiation but by the cosmological constant (see section 8.1). Figure 4.2.1 shows the evolution of the size of the universe for the three different regimes. Some of the simpler cases are derived starting in section 8.2.