8.6: Sources in General Relativity (Part 3)

Geodesic motion of test particles

Question 1 was: “Does a small enough physical object always have a world-line that is approximately a geodesic?” In other words, do Eötvös experiments give null results when carried out in laboratories using real-world apparatus of small enough size? We would like something of this type to be true, since general relativity is based on the equivalence principle, and the equivalence principle is motivated by the null results of Eötvös experiments. Nevertheless, it is fairly easy to show that the answer to the question is no, unless we make some more specific assumption, such as an energy condition, about the system being modeled.

Before we worry about energy conditions, let’s consider why the small size of the apparatus is relevant. Essentially this is because of gravitational radiation. In a gravitationally radiating system such as the Hulse-Taylor binary pulsar (section 6.2), the material bodies lose energy, and as with any radiation process, the radiated power depends on the square of the strength of the source. The world-line of a such a body therefore depends on its mass, and this shows that its world-line cannot be an exact geodesic, since the initially tangent world-lines of two different masses diverge from one another, and these two world-lines can’t both be geodesics.

Let’s proceed to give a rough argument for geodesic motion and then try to poke holes in it. When we test geodesic motion, we do an Eötvös experiment that is restricted to a certain small region of spacetime S. Our test-body’s world-line enters S with a certain energy-momentum vector p and exits with p'. If spacetime was flat, then Gauss’s theorem would hold exactly, and the vanishing divergence \(\nabla_{b}\)T^ab of the stress-energy tensor would require that the incoming flux represented by p be exactly canceled by the outgoing flux due to p'. In reality spacetime isn’t flat, and it isn’t even possible to compare p and p' except by parallel-transporting one into the same location as the other. Parallel transport is path-dependent, but if we make the reasonable restriction to paths that stay within S, we expect the ambiguity due to path-dependence to be proportional to the area enclosed by any two paths, so that if S is small enough, the ambiguity can be made small. Ignoring this small ambiguity, we can see that one way for the fluxes to cancel would be for the particle to travel along a geodesic, since both p and p' are tangent to the test-body’s world-line, and a geodesic is a curve that parallel-transports its own tangent vector. Geodesic motion is therefore one solution, and we expect the solution to be nearly unique when S is small.

Although this argument is almost right, it has some problems. First we have to ask whether “geodesic” means a geodesic of the full spacetime including the object’s own fields, or of the background spacetime B that would have existed without the object. The latter is the more sensible interpretation, since the question is basically asking whether a spacetime can really be defined geometrically, as the equivalence principle claims, based on the motion of test particles inserted into it. We also have to define words like “small enough” and “approximately;” to do this, we imagine a sequence of objects On that get smaller and smaller as n increases. We then form the following conjecture, which is meant to formulate question 1 more exactly: Given a vacuum background spacetime B, and a timelike world-line \(\ell\) in B, consider a sequence of spacetimes Sn, formed by inserting the On into B, such that: (i) the metric of S_n is defined on the same points as the metric of B; (ii) On moves along \(\ell\), and for any r > 0, there exists some n such that for m ≥ n, O_m is smaller than r;⁹ (iii) the metric of Sn approaches the metric of B as n → ∞. Then \(\ell\) is a geodesic of B.

Note

i.e., at any point P on \(\ell\), an observer moving along \(\ell\) at P defines a surface of simultaneity K passing through P, and sees the stress-energy tensor of On as vanishing outside of a three-sphere of radius r within K and centered on P

This is almost right but not quite, as shown by the following counterexample. Papapetrou¹⁰ has shown that a spinning body in a curved background spacetime deviates from a geodesic with an acceleration that is proportional to LR, where L is its angular momentum and R is the Riemann curvature. Let all the O_n have a fixed value of L, but let the spinning mass be concentrated into a smaller and smaller region as n increases, so as to satisfy (ii). As the radius r decreases, the motion of the particles composing an On eventually has to become ultrarelativistic, so that the main contribution to the gravitational field is from the particles’ kinetic energy rather than their rest mass. We then have L ∼ pr ∼ Er, so that in order to keep L constant, we must have E \(\propto \frac{1}{r}\). This causes two problems. First, it makes the gravitational field blow up at small distances, violating (iii). Also, we expect that for any known form of matter, there will come a point (probably the Tolman-Oppenheimer-Volkoff limit) at which we get a black hole; the singularity is then not part of the spacetime S_n, violating (i). But our failed counterexample can be patched up. We obtain a supply of exotic matter, whose gravitational mass is negative, and we mix enough of this mysterious stuff into each O_n so that the gravitational field shrinks rather than growing as n increases, and no black hole is ever formed.

Ehlers and Geroch¹¹ have proved that it suffices to require an additional condition: (iv) The O_n satisfy the dominant energy condition. This rules out our counterexample.

The Newtonian limit

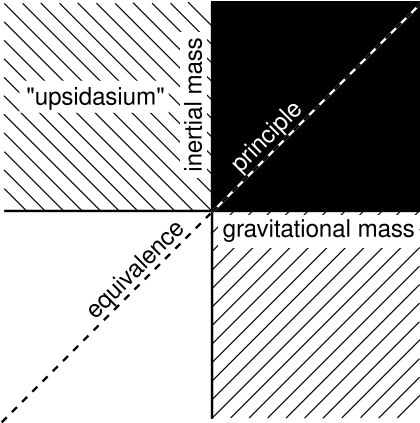
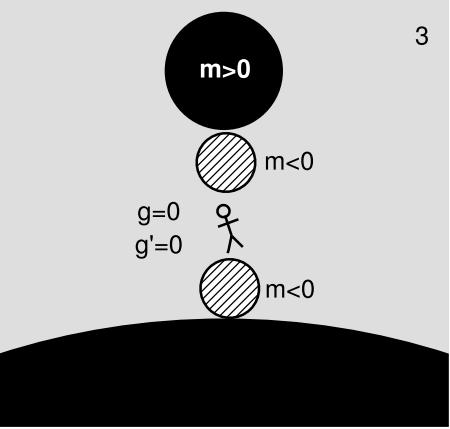
In units with c ≠ 1, a quantity like \(\rho\) + P is expressed as \(\frac{\rho + P}{c^{2}}\). The Newtonian limit is recovered as c → ∞, which makes the pressure term negligible, so that all the energy conditions reduce to \(\rho\) ≥ 0. What would it mean if this was violated? Would ρ < 0 describe an object with negative inertial mass, which would accelerate east when you pushed it to the west? Or would it describe something with negative gravitational mass, which would repel ordinary matter? We can imagine various possiblities, as shown in Figure 8.1.5. Anything that didn’t lie on the main diagonal would violate the equivalence principle, and would therefore be impossible to accomodate within general relativity’s geometrical description of gravity. If we had “upsidasium” matter such as that described by the second quadrant of the figure (example 2), gravity would be like electricity, except that like masses would attract and opposites repel; we could have gravitational dielectrics and gravitational Faraday cages. The fourth quadrant leads to amusing possibilities like Figure 8.1.6.

Figure \(\PageIndex{6}\) - Negative Mass.

Figure \(\PageIndex{7}\) - The black sphere is made of ordinary matter. The crosshatched sphere has positive gravitational mass and negative inertial mass. If the two of them are placed side by side in empty space, they will both accelerate steadily to the right, gradually approaching the speed of light. Conservation of momentum is preserved, because the exotic sphere has leftward momentum when it moves to the right, so the total momentum is always zero.

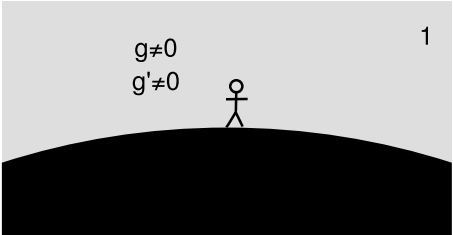
Example 10: no gravitational shielding

Electric fields can be completely excluded from a Faraday cage, and magnetic fields can be very strongly blocked with high-permeability materials such as mu-metal. It would be fun if we could do the same with gravitational fields, so that we could have zero-gravity or near-zero-gravity parties in a specially shielded room. It would be a form of antigravity, but a different one than the “upsidasium” type. Unfortunately this is difficult to do, and the reason it’s difficult turns out to be related to the unavailability of materials that violate energy conditions.

First we need to define what we mean by shielding. We restrict ourselves to the Newtonian limit, and to one dimension, so that a gravitational field is specified by a function of one variable g(x). The best kind of shielding would be some substance that we could cut with shears and form into a box, and that would exclude gravitational fields from the interior of the box. This would be analogous to a Faraday cage; no matter what external field it was embedded in, it would spontaneously adjust itself so that the internal field was canceled out. A less desirable kind of shielding would be one that we could set up on an ad hoc basis to null out a specific, given, externally imposed field. Once we know what the external field is, we try to choose some arrangement of masses such that the field is nulled out. We will show that even this kind of shielding is unachievable, if nulling out the field is interpreted to mean this: at some point, which for convenience we take to be the origin, we wish to have a gravitational field such that g(0) = 0, \(\frac{dg}{dx(0)}\) = 0, . . . \(\frac{d^{n} g}{dx^{n} (0)}\) = 0, where n is arbitrarily specified. For comparison, magnetic fields can be nulled out according to this definition by building an appropriately chosen configuration of coils such as a Helmholtz coil.

Since we’re only doing the Newtonian limit, the gravitational field is the sum of the fields made by all the sources, and we can take this as a sum over point sources. For a point source m placed at x₀, the field g(x) is odd under reflection about x₀. The derivative of the field g'(x) is even. Since g' is even, we can’t control its sign at x = 0 by choosing x₀ > 0 or x₀ < 0. The only way to control the sign of g' is by choosing the sign of m. Therefore if the sign of the externally imposed field’s derivative is wrong, we can never null it out. Figure 8.1.8 shows a special case of this theorem. The theorem does not apply to three dimensions, and it does not prove that all fields are impossible to null out, only that some are. For example, the field inside a hemispherical shell can be nulled by adding another hemispherical shell to complete the sphere. I thank P. Allen for helpful discussion of this topic.

Figure_8.1.8b.png" />

Figure \(\PageIndex{8}\) - Nulling out a gravitational field is impossible in one dimension without exotic matter. 1. The planet imposes a nonvanishing gravitational field with a nonvanishing gradient. 2. We can null the field at one point in space, by placing a sphere of very dense, but otherwise normal, matter overhead. The stick figure still experiences a tidal force, g' ≠ 0. 3. To change the field’s derivative without changing the field, we can place two additional masses above and below the given point. But to change its derivative in the desired direction — toward zero — we would have to make these masses negative.

Singularity Theorems

An important example of the use of the energy conditions is that Hawking and Ellis have proved that under the assumption of the strong energy condition, any body that becomes sufficiently compact will end up forming a singularity. We might imagine that the formation of a black hole would be a delicate thing, requiring perfectly symmetric initial conditions in order to end up with the perfectly symmetric Schwarzschild metric. Many early relativists thought so, for good reasons. If we look around the universe at various scales, we find that collisions between astronomical bodies are extremely rare. This is partly because the distances are vast compared to the sizes of the objects, but also because conservation of angular momentum has a tendency to make objects swing past one another rather than colliding head-on. Starting with a cloud of objects, e.g., a globular cluster, Newton’s laws make it extremely difficult, regardless of the attractive nature of gravity, to pick initial conditions that will make them all collide the future. For one thing, they would have to have exactly zero total angular momentum.

Most relativists now believe that this is not the case. General relativity describes gravity in terms of the tipping of light cones. When the field is strong enough, there is a tendency for the light cones to tip over so far that the entire future light-cone points at the source of the field. If this occurs on an entire surface surrounding the source, it is referred to as a trapped surface.

To make this notion of light cones “pointing at the source” more rigorous, we need to define the volume expansion \(\Theta\). Let the set of all points in a spacetime (or some open subset of it) be expressed as the union of geodesics. This is referred to as a foliation in geodesics, or a congruence. Let the velocity vector tangent to such a curve be u^a. Then we define \(\Theta = \nabla_{a} u^{a}\). This is exactly analogous to the classical notion of the divergence of the velocity field of a fluid, which is a measure of compression or expansion. Since \(\Theta\) is a scalar, it is coordinate-independent. Negative values of \(\Theta\) indicate that the geodesics are converging, so that volumes of space shrink. A trapped surface is one on which \(\Theta\) is negative when we foliate with lightlike geodesics oriented outward along normals to the surface.

When a trapped surface forms, any lumpiness or rotation in the initial conditions becomes irrelevant, because every particle’s entire future world-line lies inward rather than outward. A possible loophole in this argument is the question of whether the light cones will really tip over far enough. We could imagine that under extreme conditions of high density and temperature, matter might demonstrate unusual behavior, perhaps including a negative energy density, which would then give rise to a gravitational repulsion. Gravitational repulsion would tend to make the light cones tip outward rather than inward, possibly preventing the collapse to a singularity. We can close this loophole by assuming an appropriate energy condition. Penrose and Hawking have formalized the above argument in the form of a pair of theorems, known as the singularity theorems. One of these applies to the formation of black holes, and another one to cosmological singularities such as the Big Bang.

In a cosmological model, it is natural to foliate using worldlines that are at rest relative to the Hubble flow (or, equivalently, the world-lines of observers who see a vanishing dipole moment in the cosmic microwave background). The \(\Theta\) we then obtain is positive, because the universe is expanding. The volume expansion is \(\Theta\) = 3H₀, where H₀ ≈ 2.3 × 10⁻¹⁸ s⁻¹ is the Hubble constant (the fractional rate of change of the scale factor of cosmological distances). The factor of three occurs because volume is proportional to the cube of the linear dimensions.

Current status

The current status of the energy conditions is shaky. Although it is clear that all of them hold in a variety of situations, there are strong reasons to believe that they are violated at both microscopic and cosmological scales, for reasons both classical and quantummechanical.¹² We will see such a violation in the following section.

The Cosmological Constant

Having included the source term in the Einstein field equations, our most important application will be to cosmology. Some of the relevant ideas originate long before Einstein. Once Newton had formulated a theory of gravity as a universal attractive force, he realized that there would be a tendency for the universe to collapse. He resolved this difficulty by assuming that the universe was infinite in spatial extent, so that it would have no center of symmetry, and therefore no preferred point to collapse toward. The trouble with this argument is that the equilibrium it describes is unstable. Any perturbation of the uniform density of matter breaks the symmetry, leading to the collapse of some pocket of the universe. If the radius of such a collapsing region is r, then its gravitational is proportional to r³, and its gravitational field is proportional to \(\frac{r^{3}}{r^{2}}\) = r. Since its acceleration is proportional to its own size, the time it takes to collapse is independent of its size. The prediction is that the universe will have a self-similar structure, in which the clumping on small scales behaves in the same way as clumping on large scales; zooming in or out in such a picture gives a landscape that appears the same. With modern hindsight, this is actually not in bad agreement with reality. We observe that the universe has a hierarchical structure consisting of solar systems, galaxies, clusters of galaxies, superclusters, and so on. Once such a structure starts to condense, the collapse tends to stop at some point because of conservation of angular momentum. This is what happened, for example, when our own solar system formed out of a cloud of gas and dust.

Einstein confronted similar issues, but in a more acute form. Newton’s symmetry argument, which failed only because of its instability, fails even more badly in relativity: the entire spacetime can simply contract uniformly over time, without singling out any particular point as a center. Furthermore, it is not obvious that angular momentum prevents total collapse in relativity in the same way that it does classically, and even if it did, how would that apply to the universe as a whole? Einstein’s Machian orientation would have led him to reject the idea that the universe as a whole could be in a state of rotation, and in any case it was sensible to start the study of relativistic cosmology with the simplest and most symmetric possible models, which would have no preferred axis of rotation.

Because of these issues, Einstein decided to try to patch up his field equation so that it would allow a static universe. Looking back over the considerations that led us to this form of the equation, we see that it is very nearly uniquely determined by the following criteria:

1. It should be consistent with experimental evidence for local conservation of energy-momentum.
2. It should satisfy the equivalence principle.
3. It should be coordinate-independent.
4. It should be equivalent to Newtonian gravity or “plain” general relativity in the appropriate limit.
5. It should not be overdetermined.

This is not meant to be a rigorous proof, just a general observation that it’s not easy to tinker with the theory without breaking it.

Example 11: A failed attempt at tinkering

As an example of the lack of “wiggle room” in the structure of the field equations, suppose we construct the scalar T^a_a, the trace of the stress-energy tensor, and try to insert it into the field equations as a further source term. The first problem is that the field equation involves rank-2 tensors, so we can’t just add a scalar. To get around this, suppose we multiply by the metric. We then have something like G_ab = c₁T_ab + c₂g_abT^c_c, where the two constants c1 and c2 would be constrained by the requirement that the theory agree with Newtonian gravity in the classical limit.

To see why this attempt fails, note that the stress-energy tensor of an electromagnetic field is traceless, T^c_c = 0. Therefore the beam of light’s coupling to gravity in the c₂ term is zero. As discussed earlier, empirical tests of conservation of momentum would therefore constrain c₂ to be \(\lesssim\)10⁻⁸.

One way in which we can change the field equation without violating any of these requirements is to add a term \(\Lambda\)g_ab, giving

\[G_{ab} = 8 \pi T_{ab} + \Lambda g_{ab}, \tag{8.1.22}\]

which is what we will refer to as the Einstein field equation.¹³ As we’ll see in example 12, this is consistent with conservation of energy-momentum (requirement 1 above) if and only if \(\Lambda\) is constant. In example 13 we find that its effects are only significant on the largest scales, which makes it undetectable, for example, in solar-system tests (criterion 4). For these reasons Λ is referred to as the cosmological constant. As we’ll see below, Einstein introduced it in order to make a certain type of cosmology work.

Note

In books that use a − + + + metric rather then our + − − −, the sign of the cosmological constant term is reversed relative to ours.

We could also choose to absorb the \(\Lambda\)g_ab term in the field equations into the 8\(\pi\)T_ab, as if the cosmological constant term were due to some form of matter. It would then be a perfect fluid (example 4) with a negative pressure, and it would violate the strong energy condition (example 14). When we think of it this way, it’s common these days to refer to it as dark energy. But even if we think of it as analogous to a matter field, its constancy means that it has none of its own independent degrees of freedom. It can’t vibrate, rotate, flow, be compressed or rarefied, heated or cooled. It acts like a kind of energy that is automatically built in to every cubic centimeter of space. This is closely related to the fact that its contribution to the stress-energy tensor is proportional to the metric. One way of stating the equivalence principle (requirement 2 above) is that space itself does not come equipped with any other tensor besides the metric.

Einstein originally introduced a positive cosmological constant because he wanted relativity to be able to describe a static universe. To see why it would have this effect, compare its behavior with that of an ordinary fluid. When an ordinary fluid, such as the exploding air-gas mixture in a car’s cylinder, expands, it does work on its environment, and therefore by conservation of energy its own internal energy is reduced. A positive cosmological constant, however, acts like a certain amount of mass-energy built into every cubic meter of vacuum. Thus when it expands, it releases energy. Its pressure is negative.

Now consider the following semi-relativistic argument. Although we’ve already seen (section 6.2) that there is no useful way to separate the roles of kinetic and potential energy in general relativity, suppose that there are some quantities analogous to them in the description of the universe as a whole. (We’ll see below that the universe’s contraction and expansion is indeed described by a set of differential equations that can be interpreted in essentially this way.) If the universe contracts, a cubic meter of space becomes less than a cubic meter. The cosmological-constant energy associated with that volume is reduced, so some energy has been consumed. The kinetic energy of the collapsing matter goes down, and the collapse is decelerated.

Example 12: Cosmological constant must be constant

If \(\Lambda\) is thought of as a form of matter, then it becomes natural to ask whether it’s spread more thickly in some places than others: is the cosmological “constant” really constant? The following argument shows that it cannot vary. The field equations are \(G_{ab} = 8 \pi T_{ab} + \Lambda g_{ab}\). Taking the divergence of both sides, we have \(\nabla^{a} G_{ab} = 8 \pi \nabla^{a} T_{ab} + \nabla^{a} (\Lambda g_{ab})\). The left-hand side vanishes (see earlier). Since laboratory experiments have verified conservation of mass-energy to high precision for all the forms of matter represented by T, we have \(\nabla^{a} T_{ab} = 0\) as well. Applying the product rule to the term \(\nabla^{a} (\Lambda g_{ab})\), we get \(g_{ab} \nabla^{a} \Lambda + \Lambda \nabla^{a} g_{ab}\). But the covariant derivative of the metric vanishes, so the result is simply \(\nabla_{b} \Lambda\). Thus any variation in the cosmological constant over space or time violates the field equations, and the violation is equivalent to the violation we would get from a form of matter than didn’t conserve mass-energy locally.

Example 13: Cosmological constant is cosmological

The addition of the \(\Lambda\) term constitutes a change to the vacuum field equations, and the good agreement between theory and experiment in the case of, e.g., Mercury’s orbit puts an upper limit on \(\Lambda\) then implies that \(\Lambda\) must be small. For an order-of-magnitude estimate, consider that \(\Lambda\) has units of mass density, and the only parameters with units that appear in the description of Mercury’s orbit are the mass of the sun, m, and the radius of Mercury’s orbit, r. The relativistic corrections to Mercury’s orbit are on the order of v², or about 10⁻⁸, and they come out right. Therefore we can estimate that the cosmological constant could not have been greater than about (10⁻⁸)\(\frac{m}{r^{3}}\) ∼ 10⁻¹⁰ kg/m³, or it would have caused noticeable discrepancies. This is a very poor bound; if \(\Lambda\) was this big, we might even be able to detect its effects in laboratory experiments. Looking at the role played by r in the estimate, we see that the upper bound could have been made tighter by increasing r. Observations on galactic scales, for example, constrain it much more tightly. This justifies the description of \(\Lambda\) as cosmological: the larger the scale, the more significant the effect of a nonzero \(\Lambda\) would be.

Example 14: Energy conditions

Since the right-hand side of the field equation is 8\(\pi\)T_ab + \(\Lambda\)g_ab, it is possible to consider the cosmological constant as a type of matter contributing to the stress-energy tensor. We then have \(\rho\) = −P = \(\frac{\Lambda}{8 \pi}\). As described in more detail in section 8.2, we now know that \(\Lambda\) is positive. With \(\Lambda\) > 0, the weak and dominant energy conditions are both satisfied, so that in every frame of reference, \(\rho\) is positive and there is no flux of energy flowing at speeds greater than c. The negative pressure does violate the strong energy condition, meaning that the constant acts as a form of gravitational repulsion. If the cosmological constant is a product of the quantum-mechanical structure of the vacuum, then this violation is not too surprising, because quantum fields are known to violate various energy conditions. For example, the energy density between two parallel conducting plates is negative due to the Casimir effect.

References

¹⁰ Proc. Royal Soc. London A 209 (1951) 248. The relevant result is summarized in Misner, Thorne, and Wheeler, Gravitation, p. 1121.

¹¹ arxiv.org/abs/gr-qc/0309074v1

¹² Barcelo and Visser, “Twilight for the energy conditions?,” http://arxiv.org/abs/gr-qc/0205066v1.