5.2: Tidal Curvature Versus Curvature Caused by Local Sources
( \newcommand{\kernel}{\mathrm{null}\,}\)
A further complication is the need to distinguish tidal curvature from curvature caused by local sources. Figure 5.2.1 shows Comet Shoemaker-Levy, broken up into a string of fragments by Jupiter’s tidal forces shortly before its spectacular impact with the planet in 1994. Immediately after each fracture, the newly separated chunks had almost zero velocity relative to one another, so once the comet finished breaking up, the fragments’ world-lines were a sheaf of nearly parallel lines separated by spatial distances of only 1 km. These initially parallel geodesics then diverged, eventually fanning out to span millions of kilometers.

If initially parallel lines lose their parallelism, that is clearly an indication of intrinsic curvature. We call it a measure of sectional curvature, because the loss of parallelism occurs within a particular plane, in this case the (t,x) plane represented by Figure 5.2.2.
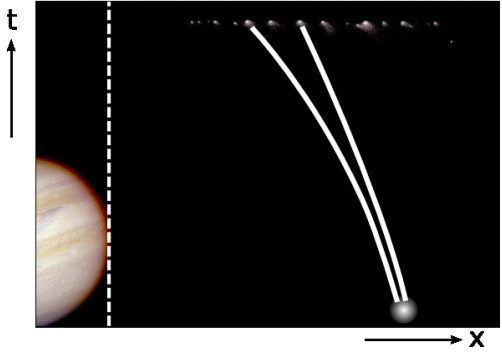
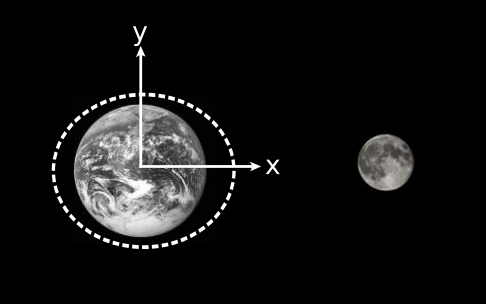
But this curvature was not caused by a local source lurking in among the fragments. It was caused by a distant source: Jupiter. We therefore see that the mere presence of sectional curvature is not enough to demonstrate the existence of local sources. Even the sign of the sectional curvature is not a reliable indication. Although this example showed a divergence of initially parallel geodesics, referred to as a negative curvature, it is also possible for tidal forces exerted by distant masses to create positive curvature. For example, the ocean tides on earth oscillate both above and below mean sea level, Figure Figure 5.2.3.
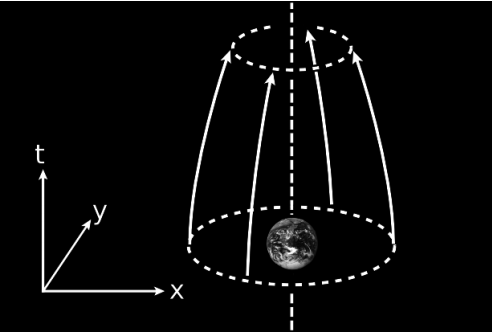
As an example that really would indicate the presence of a local source, we could release a cloud of test masses at rest in a spherical shell around the earth, and allow them to drop, Figure 5.2.4. We would then have positive and equal sectional curvature in the t−x, t−y, and t−z planes. Such an observation cannot be due to a distant mass. It demonstrates an over-all contraction of the volume of an initially parallel sheaf of geodesics, which can never be induced by tidal forces. The earth’s oceans, for example, do not change their total volume due to the tides, and this would be true even if the oceans were a gas rather than an incompressible fluid. It is a unique property of 1r2 forces such as gravity that they conserve volume in this way; this is essentially a restatement of Gauss’s law in a vacuum.