10.4: Radioactive Decay
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Describe the decay of a radioactive substance in terms of its decay constant and half-life
- Use the radioactive decay law to estimate the age of a substance
- Explain the natural processes that allow the dating of living tissue using 14C
In 1896, Antoine Becquerel discovered that a uranium-rich rock emits invisible rays that can darken a photographic plate in an enclosed container. Scientists offer three arguments for the nuclear origin of these rays. First, the effects of the radiation do not vary with chemical state; that is, whether the emitting material is in the form of an element or compound. Second, the radiation does not vary with changes in temperature or pressure—both factors that in sufficient degree can affect electrons in an atom. Third, the very large energy of the invisible rays (up to hundreds of eV) is not consistent with atomic electron transitions (only a few eV). Today, this radiation is explained by the conversion of mass into energy deep within the nucleus of an atom. The spontaneous emission of radiation from nuclei is called nuclear radioactivity (Figure 10.4.1).

Radioactive Decay Law
When an individual nucleus transforms into another with the emission of radiation, the nucleus is said to decay. Radioactive decay occurs for all nuclei with Z>82, and also for some unstable isotopes with Z<83. The decay rate is proportional to the number of original (undecayed) nuclei N in a substance. The number of nuclei lost to decay, −dN in time interval dt, is written
−dNdt=λN
where λ is called the decay constant. (The minus sign indicates the number of original nuclei decreases over time.) In other words, the more nuclei available to decay, the more that do decay (in time dt). Equation ??? can be rewritten as
dNN=−λdt.
Integrating both sides of the equation, and defining N0 to be the number of nuclei at t=0, we obtain
∫NN0dN′N=−∫t0λdt′.
This gives us
lnNN0=−λt.
Taking the left and right sides of Equation ??? as a power of e, we have the radioactive decay law.
The total number N of radioactive nuclei remaining after time t is
N=N0e−λt
where λ is the decay constant for the particular nucleus.
The total number of nuclei drops very rapidly at first, and then more slowly (Figure 10.4.2).
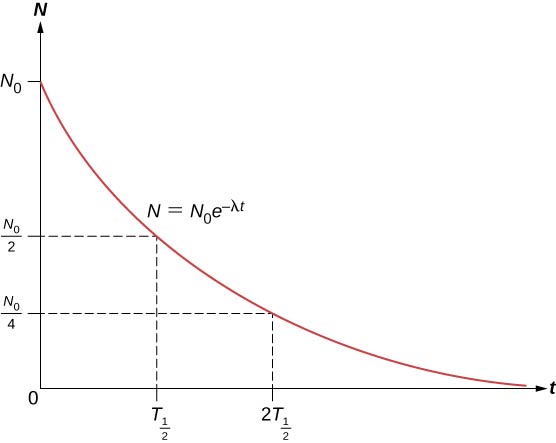
The half-life (T1/2) of a radioactive substance is defined as the time for half of the original nuclei to decay (or the time at which half of the original nuclei remain). The half-lives of unstable isotopes are shown in the chart of nuclides. The number of radioactive nuclei remaining after an integer (n) number of half-lives is therefore
N=N02n
If the decay constant (λ) is large, the half-life is small, and vice versa. To determine the relationship between these quantities, note that when t=T1/2, then N=N0/2.
Thus, Equation ??? can be rewritten as
N02=N0e−λT1/2.
Dividing both sides by N0 and taking the natural logarithm yields
ln12=lne−λT1/2
which reduces to
λ=0.693T1/2.
Thus, if we know the half-life T1/2 of a radioactive substance, we can find its decay constant. The lifetime ¯T of a radioactive substance is defined as the average amount of time that a nucleus exists before decaying. The lifetime of a substance is just the reciprocal of the decay constant, written as
¯T=1λ.
The activity A is defined as the magnitude of the decay rate, or
A=−dNdt=λN=λN0e−λt.
The infinitesimal change dN in the time interval dt is negative because the number of parent (undecayed) particles is decreasing, so the activity (A) is positive. Defining the initial activity as A0=λN0, we have
A=A0e−λt.
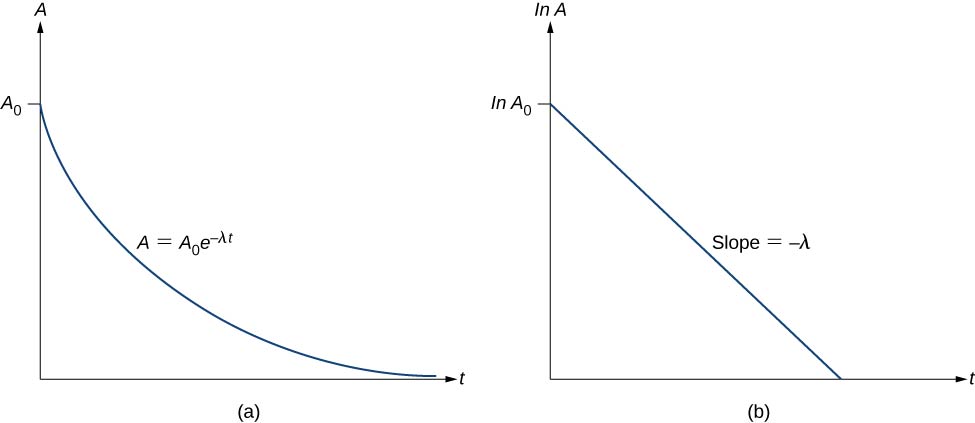
Thus, the activity A of a radioactive substance decreases exponentially with time (Figure 10.4.3).
The half-life of strontium-90, Sr9038, is 28.8 y. Find (a) its decay constant and (b) the initial activity of 1.00 g of the material.
Strategy
We can find the decay constant directly from Equation ???. To determine the activity, we first need to find the number of nuclei present.
Solution
a. The decay constant is found to be
λ=0.693T1/2=(0.693T1/2)(1yr3.16×107s)=7.61×10−10s−1.
b. The atomic mass of 9038Sr is 89.91 g. Using Avogadro’s number NA=6.022×1023 atoms/mol, we find the initial number of nuclei in 1.00 g of the material:
N0=1.00g89.91g(NA)=6.70×1021nuclei.
From this, we find that the activity A0 at t=0 for 1.00 g of strontium-90 is
A0=λN0=(7.61×10−10s−1)(6.70×1021nuclei)=5.10×1012decays/s.
Expressing λ in terms of the half-life of the substance, we get
A=A0e−(0.693/T1/2)T1/2=A0e−0.693=A0/2.
Therefore, the activity is halved after one half-life. We can determine the decay constant λ by measuring the activity as a function of time. Taking the natural logarithm of the left and right sides of Equation ???, we get
lnA=−λt+lnA0.
This equation follows the linear form y=mx+b. If we plot \ln A versus t, we expect a straight line with slope −λ and y-intercept lnA0 (Figure 10.4.3b). Activity A is expressed in units of becquerels (Bq), where one 1Bq=1decaypersecond. This quantity can also be expressed in decays per minute or decays per year. One of the most common units for activity is the curie (Ci), defined to be the activity of 1 g of 226Ra. The relationship between the Bq and Ci is
1Ci=3.70×1010Bq.
Approximately 20% of the human body by mass is carbon. Calculate the activity due to 14C in 1.00 kg of carbon found in a living organism. Express the activity in units of Bq and Ci.
Strategy
The activity of 14C is determined using the equation A0=λN0, where λ is the decay constant and N0 is the number of radioactive nuclei. The number of 14C nuclei in a 1.00-kg sample is determined in two steps. First, we determine the number of 12C nuclei using the concept of a mole. Second, we multiply this value by 1.3×10−12 (the known abundance of 14C in a carbon sample from a living organism) to determine the number of 14C nuclei in a living organism. The decay constant is determined from the known half-life of 14C (available from [link]).
Solution
One mole of carbon has a mass of 12.0 g, since it is nearly pure 12C. Thus, the number of carbon nuclei in a kilogram is
N(12C)=6.02×1023mol−112.0g/mol×(1000g)=5.02×1025.
The number of 14C nuclei in 1 kg of carbon is therefore
N(14C)=(5.02×1025)(1.3×1012)=6.52×1013.
Now we can find the activity A by using Equation ???. Entering known values gives us
A=0.693(6.52×1013)5730y=7.89×109y−1
or 7.89×109 decays per year. To convert this to the unit Bq, we simply convert years to seconds. Thus,
A=(7.89×109y−1)1.00y3.16×107s=250Bq,
or 250 decays per second. To express A in curies, we use the definition of a curie,
A=250Bq3.7×1010Bq/Ci=6.76×10−9Ci.
Thus,
A=6.76nCi.
Significance
Approximately 20% of the human body by weight is carbon. Hundreds of 14C decays take place in the human body every second. Carbon-14 and other naturally occurring radioactive substances in the body compose a person’s background exposure to nuclear radiation. As we will see later in this chapter, this activity level is well below the maximum recommended dosages.
Radioactive Dating
Radioactive dating is a technique that uses naturally occurring radioactivity to determine the age of a material, such as a rock or an ancient artifact. The basic approach is to estimate the original number of nuclei in a material and the present number of nuclei in the material (after decay), and then use the known value of the decay constant λ and Equation ???to calculate the total time of the decay, t.
An important method of radioactive dating is carbon-14 dating. Carbon-14 nuclei are produced when high-energy solar radiation strikes 14N nuclei in the upper atmosphere and subsequently decay with a half-life of 5730 years. Radioactive carbon has the same chemistry as stable carbon, so it combines with the ecosphere and eventually becomes part of every living organism. Carbon-14 has an abundance of 1.3 parts per trillion of normal carbon. Therefore, if you know the number of carbon nuclei in an object, you multiply that number by 1.3×10−12 to find the number of 14C nuclei in that object. When an organism dies, carbon exchange with the environment ceases, and 14C is not replenished as it decays.
By comparing the abundance of 14C in an artifact, such as mummy wrappings, with the normal abundance in living tissue, it is possible to determine the mummy’s age (or the time since the person’s death). Carbon-14 dating can be used for biological tissues as old as 50,000 years, but is generally most accurate for younger samples, since the abundance of 14C nuclei in them is greater. Very old biological materials contain no 14C at all. The validity of carbon dating can be checked by other means, such as by historical knowledge or by tree-ring counting.
In an ancient burial cave, your team of archaeologists discovers ancient wood furniture. Only 80% of the original 14C remains in the wood. How old is the furniture?
Strategy
The problem statement implies that N/N0=0.80. Therefore, we rearrange Equation ??? to find the product, λt. We know the half-life of 14C is 5730 y, so we also know the decay constant, and therefore the total decay time t.
Solution
We rearrange Equation ??? for N/N0 to gives
NN0=e−λt.
Thus
0.80=e−λt.
Taking the natural logarithm of both sides yields
ln0.80=−λt,
so that
−0.223=−λt.
Rearranging the equation to isolate t gives us
t=0.223(0.6935730y)=1844y.
Significance
The furniture is almost 2000 years old—an impressive discovery. The typical uncertainty on carbon-14 dating is about 5%, so the furniture is anywhere between 1750 and 1950 years old. This date range must be confirmed by other evidence, such as historical records.
A radioactive nuclide has a high decay rate. What does this mean for its half-life and activity?
- Answer
-
Half-life is inversely related to decay rate, so the half-life is short. Activity depends on both the number of decaying particles and the decay rate, so the activity can be great or small.
Visit the Radioactive Dating Game to learn about the types of radiometric dating and try your hand at dating some ancient objects.


