11.6: The Standard Model
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Describe the Standard Model in terms of the four fundamental forces and exchange particles
- Draw a Feynman diagram for a simple particle interaction
- Use Heisenberg’s uncertainty principle to determine the range of forces described by the Standard Model
- Explain the rationale behind grand unification theories
The chief intellectual activity of any scientist is the development and revision of scientific models. A particle physicist seeks to develop models of particle interactions. This work builds directly on work done on gravity and electromagnetism in the seventeenth, eighteenth, and nineteenth centuries. The ultimate goal of physics is a unified “theory of everything” that describes all particle interactions in terms of a single elegant equation and a picture. The equation itself might be complex, but many scientists suspect the idea behind the equation will make us exclaim: “How could we have missed it? It was so obvious!”
In this section, we introduce the Standard Model, which is the best current model of particle interactions. We describe the Standard Model in detail in terms of electromagnetic, weak nuclear, and strong forces. At the end of this section, we review unification theories in particle physics.
Introduction to the Standard Model
The Standard Model of particle interactions contains two ideas: electroweak theory and quantum chromodynamics (QCD) (the force acting between color charges). Electroweak theory unifies the theory of quantum electrodynamics (QED), the modern equivalent of classical electromagnetism, and the theory of weak nuclear interactions. The Standard Model combines the theory of relativity and quantum mechanics.
In the Standard Model, particle interactions occur through the exchange of bosons, the “force carriers.” For example, the electrostatic force is communicated between two positively charged particles by sending and receiving massless photons. This can occur at a theoretical infinite range. The result of these interactions is Coulomb repulsion (or attraction). Similarly, quarks bind together through the exchange of massless gluons. Leptons scatter off other leptons (or decay into lighter particles) through the exchange of massive W and Z bosons. A summary of forces as described by the Standard Model is given in Table 11.6.1. The gravitational force, mediated by the exchange of massless gravitations, is added in this table for completeness but is not part of the Standard Model.
| Force | Relative strength | Exchange particle (bosons) | Particles acted upon | Range |
|---|---|---|---|---|
| Strong | 1 | Gluon | Quarks | 10−15m |
| Electromagnetic | 1/137 | photon | Charged particles | ∞ |
| Weak | 10−10 | W+,W−,Z bosons | Quarks, leptons, neutrinos | 10−18m |
| Gravitational | 10−38 | graviton | All particles | ∞ |
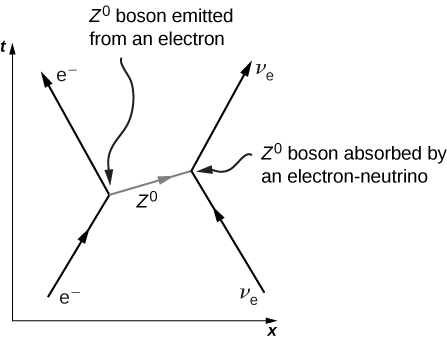
The Standard Model can be expressed in terms of equations and diagrams. The equations are complex and are usually covered in a more advanced course in modern physics. However, the essence of the Standard Model can be captured using Feynman diagrams. A Feynman diagram, invented by American physicist Richard Feynman (1918–1988), is a space-time diagram that describes how particles move and interact. Different symbols are used for different particles. Particle interactions in one dimension are shown as a time-position graph (not a position-time graph). As an example, consider the scattering of an electron and electron-neutrino (Figure 11.6.1). The electron moves toward positive values of x (to the right) and collides with an electron neutrino moving to the left. The electron exchanges a Z boson (charge zero). The electron scatters to the left and the neutrino scatters to the right. This exchange is not instantaneous. The Z boson travels from one particle to the other over a short period of time. The interaction of the electron and neutrino is said to occur via the weak nuclear force. This force cannot be explained by classical electromagnetism because the charge of the neutrino is zero. The weak nuclear force is discussed again later in this section.
Electromagnetic Force
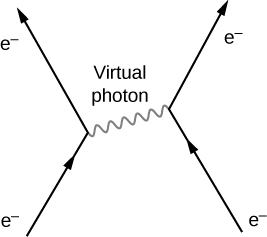
According to QED, the electromagnetic force is transmitted between charged particles through the exchange of photons. The theory is based on three basic processes: An electron travels from one place to the next, emits or absorbs a photon, and travels from one place to another again. When two electrons interact, one electron emits the photon and the other receives it (Figure 11.6.2). Photons transfer energy and momentum from one electron to the other. The net result in this case is a repulsive force. The photons exchanged are virtual. A virtual particle is a particle that exists for too short a time to be observable. Since the photon transit time Δt is extremely small, Heisenberg’s uncertainty principle states that the uncertainly in the photon’s energy, ΔE, may be very large.
To estimate the range of the electromagnetic interaction, assume that the uncertainty on the energy is comparable to the energy of the photon itself, written
ΔE≈E.
The Heisenberg uncertainly principle states that
ΔE≈hΔt.
Combining these equations, we have
Δt≈hE.
The energy of a photon is given by E=hf, so
Δt≈hhf≈1f=λc.
The distance d that the photon can move in this time is therefore
d=cΔt≈c(λc)=λ.
The energy of the virtual photon can be arbitrarily small, so its wavelength can be arbitrarily large—in principle, even infinitely large. The electromagnetic force is therefore a long-range force.
Weak Nuclear Force
The weak nuclear force is responsible for radioactive decay. The range of the weak nuclear force is very short (only about 10−18 m) and like the other forces in the Standard Model, the weak force can be described in terms of particle exchange. (There is no simple function like the Coulomb force to describe these interactions.) The particle exchanged is one of three bosons: W+, W− and Z0. The Standard Model predicts the existence of these spin-1 particles and also predicts their specific masses. In combination with previous experiments, the mass of the charged W bosons was predicted to be 81GeV/c2 and that of the Z0 was predicted to be 90GeV/c2. A CERN experiment discovered particles in the 1980s with precisely these masses—an impressive victory for the model.
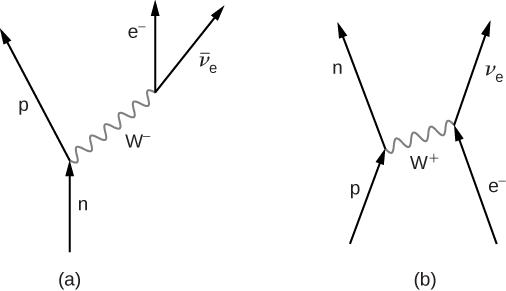
The weak nuclear force is most frequently associated with scattering and decays of unstable particles to light particles. For example, neutrons decay to protons through the weak nuclear force. This reaction is written
n→p+e−+¯νe,
where n is the neutron, p is a proton, e− is an electron, and νe is a nearly massless electron neutrino. This process, called beta decay, is important in many physical processes. A Feynman diagram of beta decay is given in Figure 11.6.3a. The neutron emits a W− and becomes a proton, then the W− produces an electron and an antineutrino. This process is similar to the scattering event
e−+p→n+νe,
In this process, the proton emits a W+ and is converted into a neutron (Figure 11.6.3b). The W+ then combines with the electron, forming a neutrino. Other electroweak interactions are considered in the exercises.
The range of the weak nuclear force can be estimated with an argument similar to the one before. Assuming the uncertainty on the energy is comparable to the energy of the exchange particle by (E≈mc2), we have
Δt≈hmc2.
The maximum distance d that the exchange particle can travel (assuming it moves at a speed close to c) is therefore
d≈cΔt=hmc.
For one of the charged vector bosons with mc2≈80GeV=1.28×10−8J, we obtain mc=4.27×10−17J⋅s/m. Hence, the range of the force mediated by this boson is ≈1.5×10−17m
Strong Nuclear Force
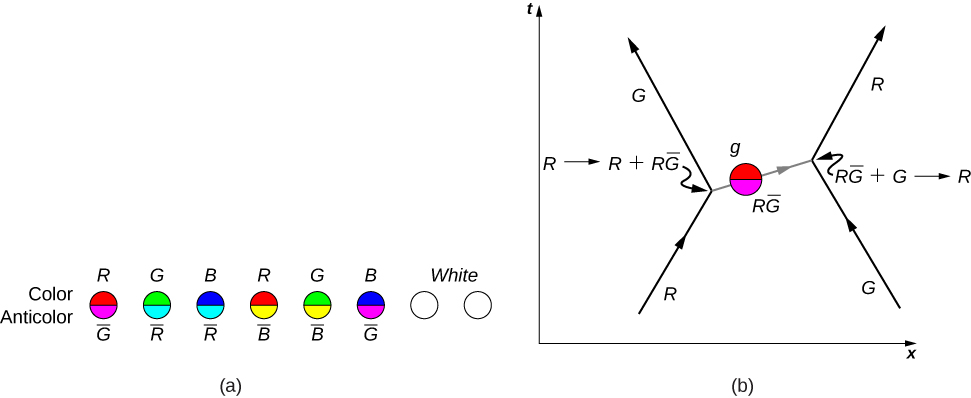
Strong nuclear interactions describe interactions between quarks. Details of these interactions are described by QCD. According to this theory, quarks bind together by sending and receiving gluons. Just as quarks carry electric charge [either (+2/3)e or (−1/3)e that determines the strength of electromagnetic interactions between the quarks, quarks also carry “color charge” (either red, blue, or green) that determines the strength of strong nuclear interactions. As discussed before, quarks bind together in groups in color neutral (or “white”) combinations, such as red-blue-green and red-antired.
Interestingly, the gluons themselves carry color charge. Eight known gluons exist: six that carry a color and anticolor, and two that are color neutral (Figure 11.6.4a). To illustrate the interaction between quarks through the exchange of charged gluons, consider the Feynman diagram in Figure 11.6.4b. As time increases, a red down quark moves right and a green strange quark moves left. (These appear at the lower edge of the graph.) The up quark exchanges a red-antigreen gluon with the strange quark. (Anticolors are shown as secondary colors. For example, antired is represented by cyan because cyan mixes with red to form white light.) According to QCD, all interactions in this process—identified with the vertices—must be color neutral. Therefore, the down quark transforms from red to green, and the strange quark transforms from green to red.
As suggested by this example, the interaction between quarks in an atomic nucleus can be very complicated. Figure 11.6.5 shows the interaction between a proton and neutron. Notice that the proton converts into a neutron and the neutron converts into a proton during the interaction. The presence of quark-antiquark pairs in the exchange suggest that bonding between nucleons can be modeled as an exchange of pions.

In practice, QCD predictions are difficult to produce. This difficulty arises from the inherent strength of the force and the inability to neglect terms in the equations. Thus, QCD calculations are often performed with the aid of supercomputers. The existence of gluons is supported by electron-nucleon scattering experiments. The estimated quark momenta implied by these scattering events are much smaller than we would expect without gluons because the gluons carry away some of the momentum of each collision.
Unification Theories
Physicists have long known that the strength of an interaction between particles depends on the distance of the interaction. For example, two positively charged particles experience a larger repulsive force at a short distance then at a long distance. In scattering experiments, the strength of an interaction depends on the energy of the interacting particle, since larger energy implies both closer and stronger interactions.
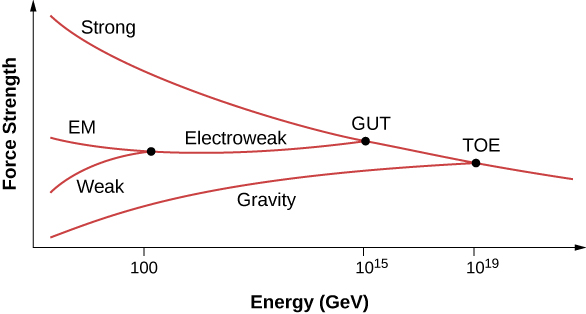
Particle physicists now suspect that the strength of all particle interactions (the four forces) merge at high energies, and the details of particle interactions at these energies can be described in terms of a single force (Figure 11.6.6). A unified theory describes what these interactions are like and explains why this description breaks down at low-energy scales. A grand unified theory is a theory that attempts to describe strong and electroweak interaction in terms of just one force. A theory of everything (TOE) takes the unification concept one step further. A TOE combines all four fundamental forces (including gravity) into one theory.


