6.3: Lee-Yang Theory
( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand\Dalpha
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Dbeta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Dgamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Ddelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Depsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Dvarepsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Dzeta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Deta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Dtheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Dvartheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Diota
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Dkappa
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Dlambda
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Dvarpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\DGamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\DDelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\DTheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vmu
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vnu
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vxi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vom
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vrho
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarrho
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vsigma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarsigma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vtau
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vupsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vphi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarphi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vchi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vpsi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\Vomega
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\VGamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\VDelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\newcommand\BI{\mib I}}
\)
\newcommand { M}
\newcommand { m}
}
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
1$#1_$
\newcommand\SZ{\textsf Z}} \( \newcommand\kFd{k\ns_{\RF\dar}\)
\newcommand\mutB{\tilde\mu}\ns_\ssr{B}
\( \newcommand\xhihOZ
Callstack:
at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
\( \newcommand\labar
Callstack:
at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.03:_Lee-Yang_Theory), /content/body/p/span, line 1, column 23
Analytic Properties of the Partition Function
How can statistical mechanics describe phase transitions? This question was addressed in some beautiful mathematical analysis by Lee and Yang7. Consider the grand partition function Ξ,
Ξ(T,V,z)=∞∑N=0zNQ∗N(T,V)λ−dNT ,
where
Q∗N(T,V)=1N!∫ddx∗1⋯∫ddx∗Ne−U(x∗1,…,x∗N)/kBT
is the contribution to the N-particle partition function from the potential energy U (assuming no momentum-dependent potentials). For two-body central potentials, we have
U(x∗1,…,x∗N)=∑i<jv(|x∗i−x∗j|).
Suppose further that these classical particles have hard cores. Then for any finite volume, there must be some maximum number N∗V such that Q∗N(T,V) vanishes for N>N∗V. This is because if N>N∗V at least two spheres must overlap, in which case the potential energy is infinite. The theoretical maximum packing density for hard spheres is achieved for a hexagonal close packed (HCP) lattice8, for which f†HCP=π3√2=0.74048. If the spheres have radius r∗0, then N∗V=V/4√2r30 is the maximum particle number.
Thus, if V itself is finite, then Ξ(T,V,z) is a finite degree polynomial in z, and may be factorized as
Ξ(T,V,z)=N∗V∑N=0zNQ∗N(T,V)λ−dNT=N∗V∏k=1(1−zz∗k) ,
where z∗k(T,V) is one of the N∗V zeros of the grand partition function. Note that the O(z0) term is fixed to be unity. Note also that since the configuration integrals Q∗N(T,V) are all positive, Ξ(z) is an increasing function along the positive real z axis. In addition, since the coefficients of zN in the polynomial Ξ(z) are all real, then Ξ(z)=0 implies ¯Ξ(z)=Ξ(ˉz)=0, so the zeros of Ξ(z) are either real and negative or else come in complex conjugate pairs.
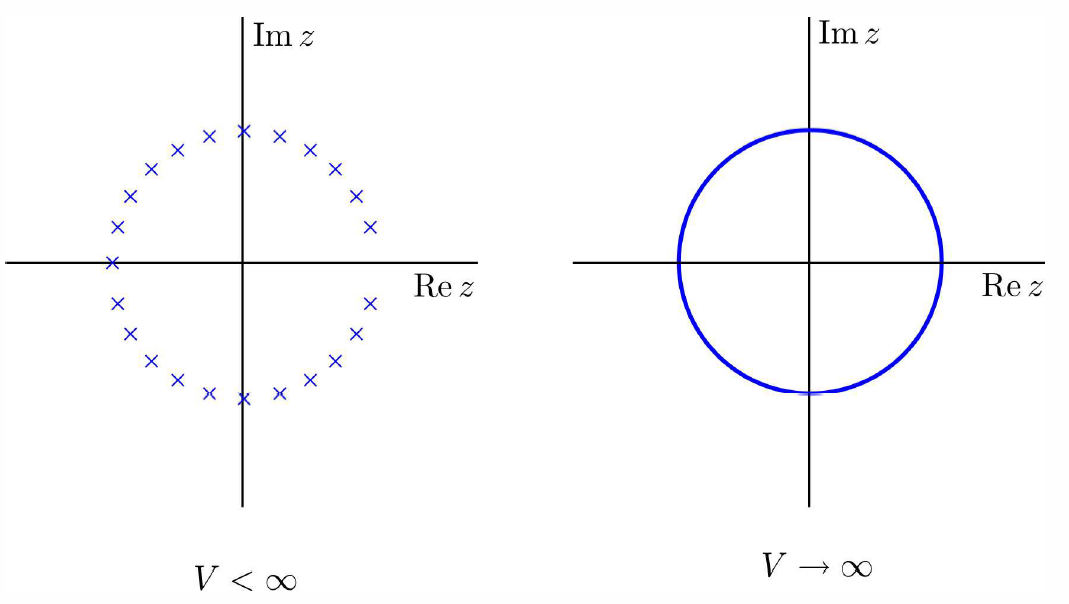
For finite N∗V, the situation is roughly as depicted in the left panel of Figure 6.3.1, with a set of N∗V zeros arranged in complex conjugate pairs (or negative real values). The zeros aren’t necessarily distributed along a circle as shown in the figure, though. They could be anywhere, so long as they are symmetrically distributed about the Re(z) axis, and no zeros occur for z real and nonnegative.
Lee and Yang proved the existence of the limits
pkBT=limV→∞1VlnΞ(T,V,z)n=limV→∞z∂∂z[1VlnΞ(T,V,z)] ,
and notably the result
n=z∂∂z(pkBT) ,
which amounts to the commutativity of the thermodynamic limit V→∞ with the differential operator z∂∂z. In particular, p(T,z) is a smooth function of z in regions free of roots. If the roots do coalesce and pinch the positive real axis, then then density n can be discontinuous, as in a first order phase transition, or a higher derivative ∂jp/∂nj can be discontinuous or divergent, as in a second order phase transition.
Electrostatic Analogy
There is a beautiful analogy to the theory of two-dimensional electrostatics. We write
pkBT=1VN∗V∑k=1ln(1−zz∗k)=−N∗V∑k=1[ϕ(z−z∗k)−ϕ(0−z∗k)] ,
where
ϕ(z)=−1Vln(z)
is the complex potential due to a line charge of linear density λ=V−1 located at origin. The number density is then
n=z∂∂z(pkBT)=−z∂∂zN∗V∑k=1ϕ(z−z∗k) ,
to be evaluated for physical values of z, z∈R+. Since ϕ(z) is analytic,
∂ϕ∂ˉz=12∂ϕ∂x+i2∂ϕ∂y=0 .
If we decompose the complex potential ϕ=ϕ∗1+iϕ∗2 into real and imaginary parts, the condition of analyticity is recast as the Cauchy-Riemann equations,
∂ϕ∗1∂x=∂ϕ∗2∂y,∂ϕ∗1∂y=−∂ϕ∗2∂x .
Thus,
−∂ϕ∂z=−12∂ϕ∂x+i2∂ϕ∂y=−12(∂ϕ∗1∂x+∂ϕ∗2∂y)+i2(∂ϕ∗1∂y−∂ϕ∗2∂x)=−∂ϕ∗1∂x+i∂ϕ∗1∂y=E∗x−iE∗y ,
where E=−∇ϕ∗1 is the electric field. Suppose, then, that as V→∞ a continuous charge distribution develops, which crosses the positive real z axis at a point x∈R+. Then
n∗+−n∗−x=E∗x(x+)−E∗x(x−)=4πσ(x) ,
where σ is the linear charge density (assuming logarithmic two-dimensional potentials), or the two-dimensional charge density (if we extend the distribution along a third axis).
Example
As an example, consider the function
Ξ(z)=(1+z)M(1−zM)1−z=(1+z)M(1+z+z2+…+zM−1) .
The (2M−1) degree polynomial has an Mth order zero at z=−1 and (M−1) simple zeros at z=e2πik/M, where k∈{1,…,M−1}. Since M serves as the maximum particle number N∗V, we may assume that V=Mv∗0, and the V→∞ limit may be taken as M→∞. We then have
pkBT=limV→∞1VlnΞ(z)=1v∗0limM→∞1MlnΞ(z)=1v∗0limM→∞1M[Mln(1+z)+ln(1−zM)−ln(1−z)] .
The limit depends on whether |z|>1 or |z|<1, and we obtain
pv∗0kBT={ln(1+z) if |z|<1[ln(1+z)+lnz] if |z|>1 .
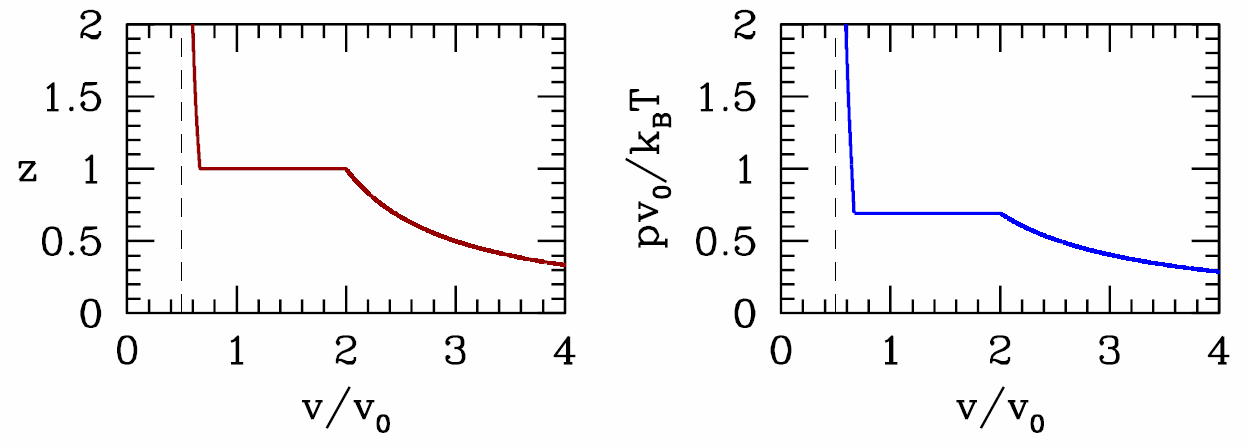
Thus,
n=z∂∂z(pkBT)={1v∗0⋅z1+z if |z|<11v∗0⋅[z1+z+1] if |z|>1 .
If we solve for z(v), where v=n−1, we find
z={v∗0v−v∗0 if v>2v∗0v∗0−v2v−v∗0 if 12v∗0<v<23v∗0 .
We then obtain the equation of state,
pv∗0kBT={ln(vv−v∗0) if v>2v∗0ln2 if 23v∗0<v<2v∗0ln(v(v∗0−v)(2v−v∗0)2) if 12v∗0<v<23v∗0 .


