6.4: Liquid State Physics
( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand\Dalpha
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Dbeta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Dgamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Ddelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Depsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Dvarepsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Dzeta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Deta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Dtheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Dvartheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Diota
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Dkappa
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Dlambda
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Dvarpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\DGamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\DDelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\DTheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vmu
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vnu
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vxi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vom
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vrho
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarrho
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vsigma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarsigma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vtau
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vupsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vphi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarphi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vchi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vpsi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\Vomega
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\VGamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\VDelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\newcommand\BI{\mib I}}
\)
\newcommand { M}
\newcommand { m}
}
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
1$#1_$
\newcommand\SZ{\textsf Z}} \( \newcommand\kFd{k\ns_{\RF\dar}\)
\newcommand\mutB{\tilde\mu}\ns_\ssr{B}
\( \newcommand\xhihOZ
Callstack:
at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
\( \newcommand\labar
Callstack:
at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.04:_Liquid_State_Physics), /content/body/p/span, line 1, column 23
The many-particle Distribution Function
The virial expansion is typically applied to low-density systems. When the density is high, when na3∼1, where a is a typical molecular or atomic length scale, the virial expansion is impractical. There are to many terms to compute, and to make progress one must use sophisticated resummation techniques to investigate the high density regime.
To elucidate the physics of liquids, it is useful to consider the properties of various correlation functions. These objects are derived from the general N-body Boltzmann distribution,
f(x†1,…,x†N;p†1,…,p†N)={Z−1N⋅1N!e−βˆH∗N(p,x)OCEΞ−1⋅1N!eβμNe−βˆH∗N(p,x)GCE .
We assume a Hamiltonian of the form
ˆH∗N=N∑i=1p2i2m+W(x∗1,…,x∗N).
The quantity
f(x†1,…,x†N;p†1,…,p†N)ddx∗1ddp∗1hd⋯ddx∗Nddp∗Nhd
is the propability of finding N particles in the system, with particle #1 lying within d3x∗1 of x∗1 and having momentum within ddp∗1 of p†1, If we compute averages of quantities which only depend on the positions {x∗j} and not on the momenta {p∗j}, then we may integrate out the momenta to obtain, in the OCE,
P(x∗1,…,x∗N)=Q−1N⋅1N!e−βW(x∗1,…,x∗N) ,
where W is the total potential energy,
W(x∗1,…,x∗N)=∑iv(x∗i)+∑i<ju(x∗i−x∗j)+∑i<j<kw(x∗i−x∗j,x∗j−x∗k)+… ,
and Q∗N is the configuration integral,
Q∗N(T,V)=1N!∫ddx∗1⋯∫ddx∗Ne−βW(x∗1,…,x∗N) .
We will, for the most part, consider only two-body central potentials as contributing to W, which is to say we will only retain the middle term on the RHS. Note that P(x∗1,…,x∗N) is invariant under any permutation of the particle labels.
Averages over the Distribution
To compute an average, one integrates over the distribution:
⟨F(x∗1,…,x∗N)⟩=∫ddx∗1⋯∫ddx∗NP(x∗1,…,x∗N)F(x∗1,…,x∗N) .
The overall N-particle probability density is normalized according to
∫ddx∗NP(x∗1,…,x∗N)=1 .
The average local density is
n∗1(r)=⟨∑iδ(r−x∗i)⟩=N∫ddx∗2⋯∫ddx∗NP(r,x∗2,…,x∗N) .
Note that the local density obeys the sum rule
∫ddrn∗1(r)=N .
In a translationally invariant system, n∗1=n=NV is a constant independent of position. The boundaries of a system will in general break translational invariance, so in order to maintain the notion of a translationally invariant system of finite total volume, one must impose periodic boundary conditions.
The two-particle density matrix n∗2(r∗1,r∗2) is defined by
n∗2(r∗1,r∗2)=⟨∑i≠jδ(r†1−x∗i)δ(r∗2−x∗j)⟩=N(N−1)∫ddx∗3⋯∫ddx∗NP(r∗1,r∗2,x∗3,…,x∗N) .
As in the case of the one-particle density matrix, the local density n∗1(r), the two-particle density matrix satisfies a sum rule:
∫ddr∗1∫ddr∗2n∗2(r∗1,r∗2)=N(N−1) .
Generalizing further, one defines the k-particle density matrix as
n∗k(r∗1,…,r∗k)=⟨∑i∗1⋯i∗k′δ(r†1−x∗i∗1)⋯δ(r∗k−x∗i∗k) ⟩=N!(N−k)!∫ddx∗k+1⋯∫ddx∗NP(r∗1,…,r∗k,x∗k+1,…,x∗N) ,
where the prime on the sum indicates that all the indices i∗1,…,i∗k are distinct. The corresponding sum rule is then
∫ddr∗1⋯∫ddr∗kn∗k(r∗1,…,r∗k)=N!(N−k)! .
The average potential energy can be expressed in terms of the distribution functions. Assuming only two-body interactions, we have
⟨W⟩=⟨∑i<ju(x∗i−x∗j)⟩=12∫ddr∗1∫ddr∗2u(r∗1−r∗2)⟨∑i≠jδ(r∗1−x∗i)δ(r∗2−x∗j)⟩=12∫ddr∗1∫ddr∗2u(r∗1−r∗2)n∗2(r∗1,r∗2) .
As the separations r∗ij=|r∗i−r∗j| get large, we expect the correlations to vanish, in which case
n∗k(r∗1,…,r∗k)=⟨∑i∗1⋯i∗k′δ(r†1−x∗i∗1)⋯δ(r∗k−x∗i∗k)⟩r∗ij→∞→∑i∗1⋯i∗k′⟨δ(r†1−x∗i∗1)⟩⋯⟨δ(r∗k−x∗i∗k)⟩=N!(N−k)!⋅1Nk n∗1(r∗1)⋯n∗1(r∗k)N∑N=(1−1N)(1−2N)⋯(1−k−1N)n∗1(r∗1)⋯n∗1(r∗k) .
The k-particle distribution function is defined as the ratio
g∗k(r∗1,…,r∗k)≡n∗k(r∗1,…,r∗k)n∗1(r∗1)⋯n∗1(r∗k) .
For large separations, then,
g∗k(r∗1,…,r∗k)r∗ij→∞→k−1∏j=1(1−jN) .
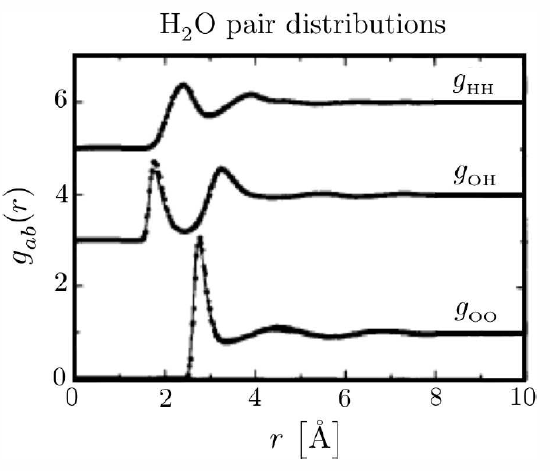
For isotropic systems, the two-particle distribution function g∗2(r∗1,r∗2) depends only on the magnitude |r∗1−r∗2|. As a function of this scalar separation, the function is known as the radial distribution function:
g(r)≡g∗2(r)=1n2⟨∑i≠jδ(r−x∗i)δ(x∗j)⟩=1Vn2⟨∑i≠jδ(r−x∗i+x∗j)⟩ .
The radial distribution function is of great importance in the physics of liquids because
- thermodynamic properties of the system can be related to g(r)
- g(r) is directly measurable by scattering experiments
For example, in an isotropic system the average potential energy is given by
⟨W⟩=12∫ddr∗1∫ddr∗2u(r∗1−r∗2)n∗2(r∗1,r∗2)=12n2∫ddr∗1∫ddr∗2u(r∗1−r∗2)g(|r∗1−r∗2|)=N22V∫ddru(r)g(r) .
For a three-dimensional system, the average internal ( potential) energy per particle is
⟨W⟩N=2πn∞∫0drr2g(r)u(r) .
Intuitively, f(r)dr≡4πr2ng(r)dr is the average number of particles lying at a radial distance between r and r+dr from a given reference particle. The total potential energy of interaction with the reference particle is then f(r)u(r)dr. Now integrate over all r and divide by two to avoid double-counting. This recovers Equation ???.

In the OCE, g(r) obeys the sum rule
∫ddrg(r)=VN2⋅N(N−1)=V−VN ,
hence
n∫ddr[g(r)−1]=−1(OCE) .
The function h(r)≡g(r)−1 is called the pair correlation function.
In the grand canonical formulation, we have
n∫d3rh(r)=⟨N⟩V⋅[⟨N(N−1)⟩⟨N⟩2V−V]=⟨N2⟩−⟨N⟩2⟨N⟩−1N∑N=nkBTκ∗T−1(GCE) ,
where κ∗T is the isothermal compressibility. Note that in an ideal gas we have h(r)=0 and κ∗T=κ0T≡1/nkBT. Self-condensed systems, such as liquids and solids far from criticality, are nearly incompressible, hence 0<nkBTκ∗T≪1, and therefore n∫d3rh(r)≈−1. For incompressible systems, where κ∗T=0, this becomes an equality.
As we shall see below in §5.4, the function h(r), or rather its Fourier transform ˆh(k), is directly measured in a scattering experiment. The question then arises as to which result applies: the OCE result from Equation ??? or the GCE result from Equation ???. The answer is that under almost all experimental conditions it is the GCE result which applies. The reason for this is that the scattering experiment typically illuminates only a subset of the entire system. This subsystem is in particle equilibrium with the remainder of the system, hence it is appropriate to use the grand canonical ensemble. The OCE results would only apply if the scattering experiment were to measure the entire system.
Virial Equation of State
The virial of a mechanical system is defined to be
G=∑ix†i⋅F†i ,
where F∗i is the total force acting on particle i. If we average G over time, we obtain
⟨G⟩=limT→∞1TT∫0dt∑ix†i⋅F†i=−limT→∞1TT∫0dt∑im˙x2i=−3NkBT .
Here, we have made use of
x∗i⋅F∗i=mx∗i⋅¨x∗i=−m˙x2i+ddt(mx∗i⋅˙x∗i) ,
as well as ergodicity and equipartition of kinetic energy. We have also assumed three space dimensions. In a bounded system, there are two contributions to the force F∗i. One contribution is from the surfaces which enclose the system. This is given by9
⟨G⟩†surfaces=⟨∑ix∗i⋅F(surf)i⟩=−3pV .
The remaining contribution is due to the interparticle forces. Thus,
pkBT=NV−13VkBT⟨∑ix∗i⋅∇∗iW⟩ .
Invoking the definition of g(r), we have
p=nkBT{1−2πn3kBT∞∫0drr3g(r)u′(r)} .
As an alternate derivation, consider the First Law of Thermodynamics,
dΩ=−SdT−pdV−Ndμ ,
from which we derive
p=−(∂Ω∂V)∗T,μ=−(∂F∂V)∗T,N .
Now let V→ℓ3V, where ℓ is a scale parameter. Then
p=−∂Ω∂V=−13V∂∂ℓ|†ℓ=1Ω(T,ℓ3V,μ) .
Now
Ξ(T,ℓ3V,μ)=∞∑N=01N!eβμNλ−3NT∫ℓ3Vd3x∗1⋯∫ℓ3Vd3x∗Ne−βW(x∗1,…,x∗N)=∞∑N=01N!(eβμλ−3T)Nℓ3N∫Vd3x∗1⋯∫Vd3x∗Ne−βW(ℓx∗1,…,ℓx∗N)
Thus,
p=−13V∂Ω(ℓ3V)∂ℓ|ℓ=1=kBT3V1Ξ∂Ξ(ℓ3V)∂ℓ=kBT3V1Ξ∞∑N=01N!(zλ−3T)N{∫Vd3x∗1⋯∫Vd3x∗Ne−βW(x∗1,…,x∗N)[3N−β∑ix∗i⋅∂W∂x∗i]}=nkBT−13V⟨∂W∂ℓ⟩†ℓ=1 .
Finally, from W=∑i<ju(ℓx∗ij) we have
⟨∂W∂ℓ⟩†ℓ=1=∑i<jx∗ij⋅∇u(x∗ij)=2πN2V∞∫0drr3g(r)u′(r) ,
and hence
p=nkBT−23πn2∞∫0drr3g(r)u′(r) .
Note that the density n enters the equation of state explicitly on the RHS of the above equation, but also implicitly through the pair distribution function g(r), which has implicit dependence on both n and T.
Correlations and Scattering
Consider the scattering of a light or particle beam ( photons or neutrons) from a liquid. We label the states of the beam particles by their wavevector k and we assume a general dispersion ε∗k. For photons, ε∗k=ℏc|k|, while for neutrons ε∗k=ℏ2k2/2m∗n. We assume a single scattering process with the liquid, during which the total momentum and energy of the liquid plus beam are conserved. We write
k′=k+qε∗k′=ε∗k+ℏω ,
where k′ is the final state of the scattered beam particle. Thus, the fluid transfers momentum Δp=ℏq and energy ℏω to the beam.
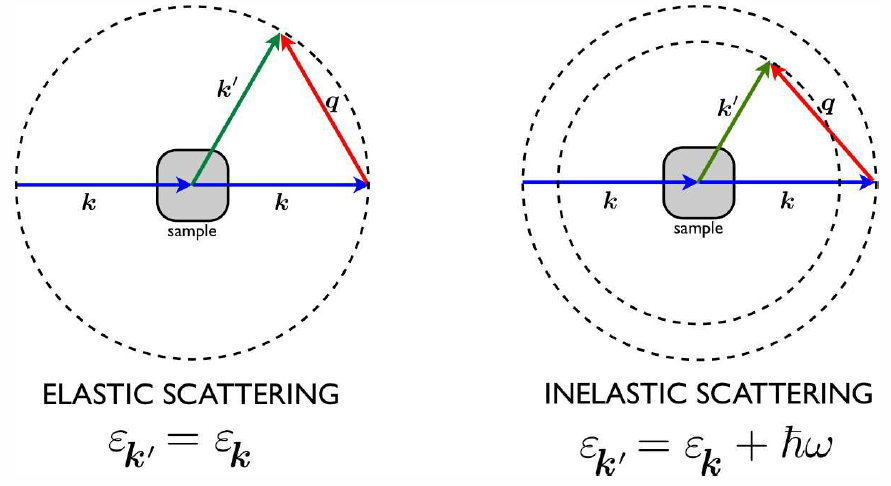
Now consider the scattering process between an initial state |i,k⟩ and a final state |j,k′⟩, where these states describe both the beam and the liquid. According to Fermi’s Golden Rule, the scattering rate is
Γ∗ik→jk′=2πℏ|⟨j,k′|V|i,k⟩|2δ(E∗j−E∗i+ℏω) ,
where V is the scattering potential and E∗i is the initial internal energy of the liquid. If r is the position of the beam particle and {x∗l} are the positions of the liquid particles, then
V(r)=N∑l=1v(r−x∗l) .
The differential scattering cross section (per unit frequency per unit solid angle) is
∂2σ∂Ω∂ω=ℏ4πg(ε∗k′)|v∗k|∑i,jP∗iΓ∗ik→jk′ ,
where
g(ε)=∫ddk(2π)dδ(ε−ε∗k)
is the density of states for the beam particle and
P∗i=1Ze−βE∗i .
Consider now the matrix element
⟨j,k′|V|i,k⟩=⟨j|1VN∑l=1∫ddrei(k−k′)⋅rv(r−x∗l)|i⟩=1Vˆv(q)⟨j|N∑l=1e−iq⋅x∗l|i⟩ ,
where we have assumed that the incident and scattered beams are plane waves. We then have
∂2σ∂Ω∂ω=ℏ2g(ε∗k+q)|∇†kε∗k||ˆv(q)|2V2∑iP∗i ∑j|⟨j|N∑l=1e−iq⋅x∗l|i⟩|2δ(E∗j−E∗i+ℏω)=g(ε∗k+q)4π|∇†kε∗k|NV2|ˆv(q)|2S(q,ω) ,
where S(q,ω) is the dynamic structure factor,
S(q,ω)=2πℏN∑iP∗i ∑j|⟨j|N∑l=1e−iq⋅x∗l|i⟩|2δ(E∗j−E∗i+ℏω)
Note that for an arbitrary operator A,
∑j|⟨j|A|i⟩|2δ(E∗j−E∗i+ℏω)=12πℏ∑j∞∫−∞dtei(E∗j−E∗i+ℏω)t/ℏ⟨i|A†|j⟩⟨j|A|i⟩=12πℏ∑j∞∫−∞dteiωt⟨i|A†|j⟩⟨j|eiˆHt/ℏAe−iˆHt/ℏ|i⟩=12πℏ∞∫−∞dteiωt⟨i|A†(0)A(t)|i⟩ .
Thus,
S(q,ω)=1N∞∫−∞dteiωt∑iP∗i⟨i|∑l,l′eiq⋅x∗l(0)e−iq⋅x∗l′(t)|i⟩=1N∞∫−∞dteiωt⟨∑l,l′eiq⋅x∗l(0)e−iq⋅x∗l′(t)⟩ ,
where the angular brackets in the last line denote a thermal expectation value of a quantum mechanical operator. If we integrate over all frequencies, we obtain the equal time correlator,
S(q)=∞∫−∞dω2πS(q,ω)=1N∑l,l′⟨eiq⋅(x∗l−x∗l′)⟩=Nδ∗q,0+1+n∫ddre−iq⋅r[g(r)−1] .
known as the static structure factor10. Note that S(q=0)=N, since all the phases eiq⋅(x∗i−x∗j) are then unity. As q→∞, the phases oscillate rapidly with changes in the distances |x∗i−x∗j|, and average out to zero. However, the ‘diagonal’ terms in the sum, those with i=j, always contribute a total of 1 to S(q). Therefore in the q→∞ limit we have S(q→∞)=1.
In general, the detectors used in a scattering experiment are sensitive to the energy of the scattered beam particles, although there is always a finite experimental resolution, both in q and ω. This means that what is measured is actually something like
S∗meas(q,ω)=∫ddq′∫dω′F(q−q′)G(ω−ω′)S(q′,ω′) ,
where F and G are essentially Gaussian functions of their argument, with width given by the experimental resolution. If one integrates over all frequencies ω, if one simply counts scattered particles as a function of q but without any discrimination of their energies, then one measures the static structure factor S(q). Elastic scattering is determined by S(q,ω=0, no energy transfer.

Correlation and Response
Suppose an external potential v(x) is also present. Then
P(x∗1,…,x∗N)=1Q∗N[v]⋅1N!e−βW(x∗1,…,x∗N)e−β∑iv(x∗i) ,
where
Q∗N[v]=1N!∫ddx∗1⋯∫ddx∗Ne−βW(x∗1,…,x∗N)e−β∑iv(x∗i) .
The Helmholtz free energy is then
F=−1βln(λ−dNTQ∗N[v]) .
Now consider the functional derivative
δFδv(r)=−1β⋅1Q∗N⋅δQ†Nδv(r) .
Using
∑iv(x∗i)=∫ddrv(r)∑iδ(r−x∗i) ,
hence
δFδv(r)=∫ddx∗1⋯∫ddx∗NP(x∗1,…,x∗N)∑iδ(r−x∗i)=n∗1(r) ,
which is the local density at r.
Next, consider the response function,
χ(r,r′)≡δn∗1(r)δv(r′)=δ2F[v]δv(r)δv(r′)=1β⋅1Q2NδQ∗Nδv(r)δQ∗Nδv(r′)−1β⋅1Q∗Nδ2Q∗Nδv(r)δv(r′)N∑N=βn∗1(r)n∗1(r′)−βn∗1(r)δ(r−r′)−βn∗2(r,r′) .
In an isotropic system, \xhi(\Br,\Br')=\xhi(\Br-\Br') is a function of the coordinate separation, and
\begin{split} -\kT\,\chi(\Br-\Br')&=-n^2 + n\,\delta(\Br-\Br') + n^2 g\big(|\Br-\Br'|\big)\bvph\\ &=n^2\,h\big(|\Br-\Br'|\big) + n\,\delta(\Br-\Br')\ . \end{split}
Taking the Fourier transform,
-\kT\,{\hat\chi}(\Bq)=n+n^2\,{\hat h}(\Bq)=n \,S(\Bq)\ .
We may also write
{\kappa\ns_T\over\kappa^0_T}=1+n\,{\hat h}(0)=-n\kT\,{\hat\chi}(0)\ ,
\kappa\ns_T=-\Hxhi(0).
What does this all mean? Suppose we have an isotropic system which is subjected to a weak, spatially inhomogeneous potential v(\Br). We expect that the density n(\Br) in the presence of the inhomogeneous potential to itself be inhomogeneous. The first corrections to the v=0 value n=n_0 are linear in v, and given by
\begin{split} \delta n(\Br)&=\int\!\!d^d\!r'\>\xhi(\Br,\Br')\, v(\Br')\\ &=-\beta n_0\, v(\Br) - \beta n_0^2\!\int\!\!d^d\!r'\>h(\Br-\Br)\, v(\Br')\ . \end{split}
Note that if v(\Br)>0 it becomes energetically more costly for a particle to be at \Br. Accordingly, the density response is negative, and proportional to the ratio v(\Br)/\kT – this is the first term in the above equation. If there were no correlations between the particles, then h=0 and this would be the entire story. However, the particles in general are correlated. Consider, for example, the case of hard spheres of diameter a, and let there be a repulsive potential at \Br=0. This means that it is less likely for a particle to be centered anywhere within a distance a of the origin. But then it will be more likely to find a particle in the next ‘shell’ of radial thickness a.
BBGKY Hierarchy
The distribution functions satisfy a hierarchy of integro-differential equations known as the BBGKY hierarchy11. In homogeneous systems, we have
g\ns_k(\rok)={N!\over (N-k)!}\,{1\over n^k}\!\int\!\!d^d\!x\ns_{k+1}\cdots\!\int\!\!d^d\!x\ns_N\,P(\rok\,,\,\Bx\ns_{k+1}\,,\,\ldots\,,\,\Bx\ns_N)\ ,
where
P(\xoN)={1\over Q\ns_N}\cdot{1\over N!}\>e^{-\beta W(\xoN)}\ .
Taking the gradient with respect to \Br\ns_1, we have
\begin{split} {\pz\over\pz\Br\ns_1}g\ns_k(\rok)&={1\over Q\ns_N}\cdot{n^{-k}\over (N-k)!}\!\int\!\!d^d\!x\ns_{k+1}\cdots\!\int\!\!d^d\!x\ns_N\, e^{-\beta\sum_{k<i<j}u(\Bx\ns_{ij})}\\ &\qquad\qquad\times{\pz\over\pz\Br\ns_1}\bigg[ e^{-\beta\sum_{i<j\le k} u(\Br\ns_{ij})}\cdot e^{-\beta\sum_{i\le k < j}u(\Br\ns_i-\Bx\ns_j)}\bigg]\ , \end{split}
where \sum_{k<i<j} means to sum on indices i and j such that i<j and k<i,
\begin{aligned} \sum_{k<i<j}u(\Bx\ns_{ij})&\equiv \sum_{i=k+1}^{N-1} \sum_{j=i+1}^Nu\big(\Bx\ns_i-\Bx\ns_j\big)\\ \sum_{i<j\le k}u(\Br\ns_{ij})&\equiv \sum_{i=1}^{k-1} \sum_{j=i+1}^k u\big(\Br\ns_i-\Br\ns_j\big)\\ \sum_{i\le k < j}u(\Br\ns_i-\Bx\ns_j)&=\sum_{i=1}^k \sum_{j=k+1}^N u(\Br\ns_i-\Bx\ns_j)\ .\end{aligned}
Now
\begin{split} {\pz\over\pz\Br\ns_1}\bigg[ e^{-\beta\sum_{i<j\le k} u(r\ns_{ij})}\cdot e^{-\beta\sum_{i\le k < j}u(\Br\ns_i-\Bx\ns_j)}\bigg]=\\ &\hskip-2.4in\beta\>\Bigg\{\!\sum_{1<j\le k} {\pz u(\Br\ns_1-\Br\ns_j)\over\pz\Br\ns_1}\ + \sum_{k<j} {\pz u(\Br\ns_1-\Br\ns_j)\over\pz\Br\ns_1}\Bigg\} \cdot\bigg[ e^{-\beta\sum_{i<j\le k} u(r\ns_{ij})}\cdot e^{-\beta\sum_{i\le k < j}u(\Br\ns_i-\Bx\ns_j)}\bigg]\ \ , \end{split}
hence
\begin{split} {\pz\over\pz\Br\ns_1}g\ns_k(\rok)&=-\beta\sum_{j=2}^k{\pz u(\Br\ns_1-\Br\ns_j)\over\pz\Br\ns_1}\,g\ns_k(\rok)\\ &\qquad-\beta(N-k)\!\int\!\!d^d\!x\ns_{k+1}\,{\pz u(\Br\ns_1-\Bx\ns_{k+1})\over\pz\Br\ns_1}\,P(\rok\,,\,\Bx\ns_{k+1}\,,\,\ldots\,,\,\Bx\ns_N)\\ &=-\beta\sum_{j=2}^k{\pz u(\Br\ns_1-\Br\ns_j)\over\pz\Br\ns_1}\,g\ns_k(\rok)\\ &\hskip1.1in +n\!\int\!\!d^d\!x\ns_{k+1}\,{\pz u(\Br\ns_1-\Bx\ns_{k+1})\over\pz\Br\ns_1}\,g\ns_{k+1}(\rok\,,\,x\ns_{k+1})\quad. \end{split}
Thus, we obtain the BBGKY hierarchy:
\begin{split} -\kT\,{\pz\over\pz\Br\ns_1}g\ns_k(\rok)&=\sum_{j=2}^k{\pz u(\Br\ns_1-\Br\ns_j)\over\pz\Br\ns_1}\,g\ns_k(\rok)\\ &\qquad\qquad + n\!\int\!\!d^d\!r'\,{\pz u(\Br\ns_1-\Br')\over\pz\Br\ns_1}\,g\ns_{k+1}(\rok\,,\,\Br')\quad. \end{split}
The BBGKY hierarchy is an infinite tower of coupled integro-differential equations, relating g\ns_k to g\ns_{k+1} for all k. If we approximate g\ns_k at some level k in terms of equal or lower order distributions, then we obtain a closed set of equations which in principle can be solved, at least numerically. For example, the Kirkwood approximation closes the hierarchy at order k=2 by imposing the condition
g\ns_3(\Br\ns_1\,,\,\Br\ns_2\,,\,\Br\ns_3)\equiv g(\Br\ns_1-\Br\ns_2)\,g(\Br\ns_1-\Br\ns_3)\,g(\Br\ns_2-\Br\ns_2)\ .
This results in the single integro-differential equation
-\kT\,\bnabla g(\Br)=g(\Br)\,\bnabla u + n\!\int\!\!d^d\!r'\,g(\Br)\,g(\Br')\,g(\Br-\Br')\,\bnabla u(\Br-\Br')\ .
This is known as the Born-Green-Yvon (BGY) equation. In practice, the BGY equation, which is solved numerically, gives adequate results only at low densities.
Ornstein-Zernike Theory
The direct correlation function c(\Br) is defined by the equation
h(\Br)=c(\Br) + n\!\int\!\!d^3\!r'\>h(\Br-\Br')\,c(\Br')\ ,
where h(r)=g(r)-1 and we assume an isotropic system. This is called the Ornstein-Zernike equation. The first term, c(\Br), accounts for local correlations, which are then propagated in the second term to account for long-ranged correlations.
The OZ equation is an integral equation, but it becomes a simple algebraic one upon Fourier transforming:
{\hat h}(\Bq)={\hat c}(\Bq) + n\,{\hat h}(\Bq)\,{\hat c}(\Bq)\ ,
the solution of which is
{\hat h}(\Bq)={{\hat c}(\Bq)\over 1-n\,{\hat c}(\Bq)}\ .
The static structure factor is then
S(\Bq)=1+n\,{\hat h}(\Bq)={1\over 1-n\,{\hat c}(\Bq)}\ .
In the grand canonical ensemble, we can write
\kappa\ns_T={1+n\,{\hat h}(0)\over n\kT}={1\over n\kT}\cdot{1\over 1-n\,{\hat c}(0)} \qquad\Longrightarrow\qquad n\,{\hat c}(0)=1-{\kappa^0_T\over\kappa\ns_T}\ ,
where \kappa^0_T=1/n\kT is the ideal gas isothermal compressibility.
At this point, we have merely substituted one unknown function, h(\Br), for another, namely c(\Br). To close the system, we need to relate c(\Br) to h(\Br) again in some way. There are various approximation schemes which do just this.
Percus-Yevick Equation
In the Percus-Yevick approximation, we take
c(\Br)=\big[1-e^{\beta u(\Br)}\big]\cdot g(\Br)\ .
Note that c(\Br) vanishes whenever the potential u(\Br) itself vanishes. This results in the following integro-differential equation for the pair distribution function g(\Br):
g(\Br)=e^{-\beta u(\Br)}+n\,e^{-\beta u(\Br)}\!\int\!\!d^3\!r'\>\big[g(\Br-\Br')-1\big]\cdot\big[1-e^{\beta u(\Br')}\big]\,g(\Br')\ .
This is the Percus-Yevick equation. Remarkably, the Percus-Yevick (PY) equation can be solved analytically for the case of hard spheres, where u(r)=\infty for r\le a and u(r)=0 for r>a, where a is the hard sphere diameter. Define the function y(\Br)=e^{\beta u(\Br)}g(\Br), in which case
c(\Br)=y(\Br)\,f(\Br)=\begin{cases} -y(\Br) & ,\ r\le a \\ 0 & ,\ r>a\ . \end{cases}
Here, f(\Br)=e^{-\beta u(\Br)}-1 is the Mayer function. We remark that the definition of y(\Br) may cause some concern for the hard sphere system, because of the e^{\beta u(\Br)} term, which diverges severely for r\le a. However, g(r) vanishes in this limit, and their product y(\Br) is in fact finite! The PY equation may then be written for the function y(\Br) as
y(\Br)=1+n\!\!\!\int\limits_{r'<a}\!\!\!\!d^3\!r'\>y(\Br')-n\!\!\!\!\!\!\!\int\limits_{r'<a\atop |\Br-\Br'|>a}\!\!\!\!\!\!\!\!d^3\!r'\>y(\Br')\,y(\Br-\Br')\ .
This has been solved using Laplace transform methods by M. S. Wertheim, J. Math. Phys. 5, 643 (1964). The final result for c(\Br) is
c(\Br)=-\left\{\lambda\ns_1 + 6\eta\,\lambda_2\,\Big({r\over a}\Big) + \half \eta\,\lambda_1\,\Big({r\over a}\Big)^3\right\}\cdot\RTheta(a-r)\ , \label{PYdcf}
where \eta=\frac{1}{6}\pi a^3 n is the packing fraction and
\lambda\ns_1={(1+2\eta)^2\over (1-\eta)^4} \qquad,\qquad\lambda_2=-{(1+\half\eta)^2\over (1-\eta)^4}\ . \label{PYlambdas}
This leads to the equation of state
p=n\kT\cdot{1+\eta+\eta^2\over (1-\eta)^3}\ . \label{PYesa}
This gets B\ns_2 and B\ns_3 exactly right. The accuracy of the PY approximation for higher order virial coefficients is shown in table [pytab].
To obtain the equation of state from Equation ref{PYdcf}, we invoke the compressibility equation,
n\kT\,\kappa\ns_T=\pabc{n}{p}{T}={1\over 1-n\,{\hat c}(0)}\ .
We therefore need
\begin{split} {\hat c}(0)&=\int\!\!d^3\!r\,c(\Br)\\ &=-4\pi a^3\!\!\int\limits_0^1\!\!dx\,x^2\,\left[\lambda\ns_1 + 6\,\eta\,\lambda\ns_2\,x + \half\,\eta\,\lambda\ns_1\,x^3\right]\\ &=-4\pi a^3\left[\frac{1}{3}\,\lambda\ns_1 + \frac{3}{2}\,\eta\,\lambda\ns_2 + \frac{1}{12}\,\eta\,\lambda\ns_1\right]\ . \end{split}
With \eta=\frac{1}{6}\pi a^3 n and using the definitions of \lambda\ns_{1,2} in Equation \ref{PYlambdas}, one finds
1-n\,{\hat c}(0)={1+4\eta+4\eta^2\over (1-\eta)^4}\ .
We then have, from the compressibility equation,
{6\kT\over \pi a^3}\,{\pz p\over\pz\eta}={1+4\eta+4\eta^2\over (1-\eta)^4}\ .
Integrating, we obtain p(\eta) up to a constant. The constant is set so that p=0 when n=0. The result is Equation \ref{PYesa}.
| quantity | exact | PY | HNC |
|---|---|---|---|
| B_4/B_2^3 | 0.28695 | 0.2969 | 0.2092 |
| B_5/B_2^4 | 0.1103 | 0.1211 | 0.0493 |
| B_6/B_2^5 | 0.0386 | 0.0281 | 0.0449 |
| B_7/B_2^6 | 0.0138 | 0.0156 | – |
Another commonly used scheme is the hypernetted chains (HNC) approximation, for which
c(\Br)=-\beta u(\Br) + h(\Br) - \ln\!\Big(1+h(\Br)\Big)\ .
The rationale behind the HNC and other such approximation schemes is rooted in diagrammatic approaches, which are extensions of the Mayer cluster expansion to the computation of correlation functions. For details and references to their application in the literature, see Hansen and McDonald (1990) and Reichl (1998).
Ornstein-Zernike Approximation at Long Wavelengths
Let’s expand the direct correlation function {\hat c}(\Bq) in powers of the wavevector \Bq, viz.
\Hc(\Bq)=\Hc(0)+c\ns_2\,q^2 + c\ns_4\,q^4 + \ldots\ .
Here we have assumed spatial isotropy. Then
\begin{split} 1-n\,\Hc(\Bq)&={1\over S(\Bq)}=1-n\,\Hc(0)-n\,c\ns_2\,q^2 + \ldots\\ &\equiv \xi^{-2} R^2+ q^2 R^2 + \CO(q^4)\ , \end{split}
where
R^2=-n\,c\ns_2 = 2\pi n\!\!\int\limits_0^\infty \!\!dr\,r^4\,c(r)
and
\xi^{-2}={1-n\,\Hc(0)\over R^2}={1-4\pi n\!\int_0^\infty\!\!dr\,r^2\,c(r)\over 2\pi n\!\int_0^\infty \!\!dr\,r^4\,c(r)}\ .
The quantity R(T) tells us something about the effective range of the interactions, while \xi(T) is the correlation length. As we approach a critical point, the correlation length diverges as a power law:
\xi(T)\sim A |T-T\ns_\Rc|^{-\nu}\ .
The susceptibility is given by
\Hxhi(\Bq)=-n\beta\, S(\Bq)=-{n\beta R^{-2}\over \xi^{-2}+ q^2 + \CO(q^4)}
In the Ornstein-Zernike approximation, one drops the \CO(q^4) terms in the denominator and retains only the long wavelength behavior. in the direct correlation function. Thus,
\xhihOZ(\Bq)=-{n\beta R^{-2}\over\xi^{-2}+q^2}\ .
We now apply the inverse Fourier transform back to real space to obtain \xhiOZ(\Br). In d=1 dimension the result can be obtained exactly:
\begin{split} \xhiOZ_{d=1}(x)&=-{n\over\kT R^2}\!\int\limits_{-\infty}^\infty\!\!{dq\over 2\pi}\>{e^{iqx}\over \xi^{-2}+q^2}\\ &=-{n\xi\over 2\kT R^2}\,e^{-|x|/\xi}\ . \end{split}
In higher dimensions d>1 we can obtain the result asymptotically in two limits:
- Take r\to \infty with \xi fixed. Then \xhiOZ_d(\Br)\simeq -C\ns_d \,n\cdot{\xi^{(3-d)/2}\over \kT\,R^2}\cdot{e^{-r/\xi}\over r^{(d-1)/2}}\cdot\left\{1+\CO\bigg({d-3\over r/\xi}\bigg)\right\}\ , where the C\ns_d are dimensionless constants.
- Take \xi\to\infty with r fixed; this is the limit T\to T\ns_\Rc at fixed r. In dimensions d>2 we obtain \xhiOZ_d(\Br)\simeq -{C'_d\, n\over\kT R^2}\cdot{e^{-r/\xi}\over r^{d-2}}\cdot \left\{1+\CO\bigg({d-3\over r/\xi}\bigg)\right\}\ . In d=2 dimensions we obtain \xhiOZ_{d=2}(\Br)\simeq-{C'_2\,n\over\kT R^2}\cdot\ln\!\bigg({r\over\xi}\bigg)\,e^{-r/\xi}\cdot\left\{1+\CO\bigg({1\over\ln(r/\xi)}\bigg)\right\}\ , where the C'_d are dimensionless constants.
At criticality, \xi\to\infty, and clearly our results in d=1 and d=2 dimensions are nonsensical, as they are divergent. To correct this behavior, M. E. Fisher in 1963 suggested that the OZ correlation functions in the r\ll \xi limit be replaced by
\xhi(\Br)\simeq -C''_d\,n \cdot {\xi^\eta\over \kT R^2}\cdot{e^{-r/\xi}\over r^{d-2+\eta}}\ ,
a result known as anomalous scaling. Here, \eta is the anomalous scaling exponent.
Recall that the isothermal compressibility is given by \kappa\ns_T=-\Hxhi(0). Near criticality, the integral in \Hxhi(0) is dominated by the r\ll\xi part, since \xi\to\infty. Thus, using Fisher’s anomalous scaling,
\begin{split} \kappa\ns_T=-\Hxhi(0)&=-\int\!\!d^d\!r\,\xhi(\Br)\\ &\sim A\!\int\!\!d^d\!r\>{e^{-r/\xi}\over r^{d-2+\eta}} \sim B\,\xi^{2-\eta}\sim C\,\big|T-T\ns_\Rc\big|^{-(2-\eta)\nu}\ , \end{split}
where A, B, and C are temperature-dependent constants which are nonsingular at T=T\ns_\Rc. Thus, since \kappa\ns_T\propto |T-T\ns_\Rc|^{-\gamma}, we conclude
\gamma=(2-\eta)\,\nu\ ,
a result known as hyperscaling.


