3.2: Work and Energy
- Page ID
- 102331
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Calculate the work done by any force.
- Calculate the kinetic energy of a particle given its mass and velocity or momentum.
- Relate the difference of potential energy to work done on a particle for a system without friction or air drag.
- Explain the meaning of the zero of the potential energy function for a system.
- Define conservative force and non-conservative force.
- Formulate the principle of conservation of mechanical energy, with or without the presence of non-conservative forces
Work
In physics, work represents a type of energy. Work is done when a force acts on something that undergoes a displacement from one position to another. Forces can vary as a function of position, and displacements can be along various paths between two points. We first define the increment of work dW done by a force \(\vec{F}\) acting through an infinitesimal displacement d\(\vec{r}\) as the dot product of these two vectors:
\[dW = \vec{F} \cdotp d \vec{r} = |\vec{F}||d \vec{r}| \cos \theta \ldotp \label{7.1}\]
Then, we can add the contributions for infinitesimal displacements along a path between two positions to get the total work.
The work done by a force is the integral of the force with respect to displacement along the path of the displacement:
\[W_{AB} = \int_{path\; AB} \vec{F} \cdotp d \vec{r} \ldotp \label{7.2}\]
The vectors involved in the definition of the work done by a force acting on a particle are illustrated in Figure \(\PageIndex{1}\).
We choose to express the dot product in terms of the magnitudes of the vectors and the cosine of the angle between them because the meaning of the dot product for work can be put into words more directly in terms of magnitudes and angles. We could equally well have expressed the dot product in terms of the various components introduced in Vectors. In two dimensions, these were the x- and y-components in Cartesian coordinates, or the r- and \(\varphi\)-components in polar coordinates; in three dimensions, it was just x-, y-, and z-components. Which choice is more convenient depends on the situation. In words, you can express Equation \ref{7.1} for the work done by a force acting over a displacement as a product of one component acting parallel to the other component. From the properties of vectors, it doesn’t matter if you take the component of the force parallel to the displacement or the component of the displacement parallel to the force—you get the same result either way.
Recall that the magnitude of a force times the cosine of the angle the force makes with a given direction is the component of the force in the given direction. The components of a vector can be positive, negative, or zero, depending on whether the angle between the vector and the component-direction is between 0° and 90° or 90° and 180°, or is equal to 90°. As a result, the work done by a force can be positive, negative, or zero, depending on whether the force is generally in the direction of the displacement, generally opposite to the displacement, or perpendicular to the displacement. The maximum work is done by a given force when it is along the direction of the displacement (cos \(\theta\) = ± 1), and zero work is done when the force is perpendicular to the displacement (cos \(\theta\) = 0).
The unit of work is units of force multiplied by units of length, which in the SI system is newtons times meters, \(\mathrm{N}\cdot\mathrm{m}\). This combination is called a joule and is abbreviated as J.
Kinetic Energy
Kinetic energy is the energy of motion. For particles with speeds slow compared to the speed of light, we can define the kinetic energy of a particle with mass \(m\) and speed \(v\) or momentum magnitude \( p = mv \).
The kinetic energy of a particle is:
\[K = \frac{1}{2} mv^{2} = \frac{p^{2}}{2m} \ldotp \label{7.6}\]
We then extend this definition to any system of particles by adding up the kinetic energies of all \(N\) of its constituent particles:
\[K =\sum_{i=1}^N \frac{1}{2} m_iv_i^{2} \ldotp \label{7.7}\]
The units of kinetic energy are joules (J).
If force is applied to a particle, it will accelerate, thereby changing its speed and kinetic energy. However, from Equation \ref{7.2}, the applied force must also do work on the particle. As a result, work and kinetic energy must be related, and this relationship is defined in the work-kinetic energy theorem.
The net work done on a particle equals the change in the particle's kinetic energy:
\[W_{net} = K_B - K_A . \label{workKEThm} \]
Potential Energy
Potential energy is "stored" energy. As an example, consider kicking a football as illustrated in Figure \(\PageIndex{1}\). For simplicity, let's ignore friction and air resistance and define our coordinate system with the vertical axis in the positive direction. As the football rises, the work done by the gravitational force on the football is negative, because the ball’s displacement is positive vertically and the force due to gravity is negative vertically. The ball slows down until it reaches its highest point in the motion, implying decreasing kinetic energy. Under the principle of conservation of energy, this loss in kinetic energy must translate into a gain in gravitational potential energy of the football-Earth system so that the total energy of the system is conserved (constant). In some sense, energy is being temporarily "stored" by gravity in the increased height of the football.
As the football falls toward Earth, the work done on the football is now positive, because the displacement and the gravitational force both point vertically downward. The ball also speeds up, which indicates an increase in kinetic energy. Therefore, energy is converted from gravitational potential energy back into kinetic energy.
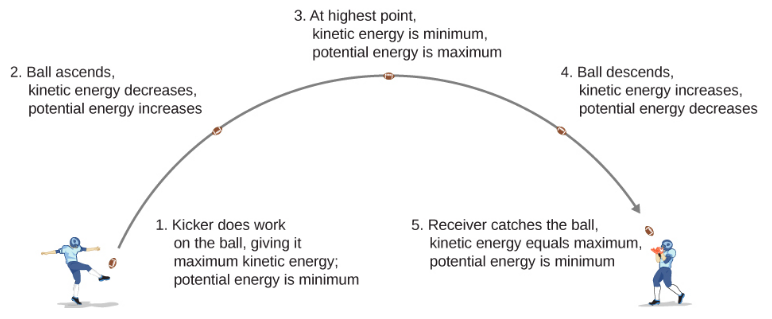
Based on this scenario, we can define the difference of potential energy from point A to point B as the negative of the work done:
\[ \Delta U_{A B}=U_{B}-U_{A}=-W_{A B} \label{8.1} \]
This formula explicitly states a potential energy difference, not just an absolute potential energy. Therefore, we need to define potential energy at a given position in such a way as to state standard values of potential energy on their own, rather than potential energy differences. We do this by rewriting the potential energy function in terms of an arbitrary constant,
\[ \Delta U=U(\overrightarrow{\mathbf{r}})-U\left(\overrightarrow{\mathbf{r}}_{0}\right) \label{8.2} \]
The choice of the potential energy at a starting location of \(\vec{r}_0\) is made out of convenience in the given problem. Most importantly, the choice should be stated and kept consistent throughout the given problem. There are some well-accepted choices of initial potential energy. For example, the lowest height in a problem is usually defined as zero potential energy, or if an object is in space, the farthest point away from the system is often defined as zero potential energy. Then, the potential energy, with respect to zero at \(\vec{r}_0\), is just \(U(\vec{r})\).
Common types of potential energy include gravitational potential energy and elastic potential energy, i.e., energy stored in compressed or extended springs. (We will see that electric charges can also have electric potential energy.)
Conservation of Energy
We can now mathematically define the concept of energy conservation.
The mechanical energy E of a particle stays constant unless forces outside the system or non-conservative forces do work on it, in which case, the change in the mechanical energy is equal to the work done by the non-conservative forces:
\[W_{nc,\; AB} = \Delta (K + U)_{AB} = \Delta E_{AB} \ldotp \label{8.12}\]
Non-conservative forces are dissipative forces such as friction or air resistance. These forces take energy away from the system as the system progresses, energy that you can’t get back. These forces are path-dependent; it matters where the object starts and stops. Conservative forces are forces for which the change in energy is path-independent. Gravity is an example of a conservative force. Conservative forces can have a potential energy associated with them. (We will see that the electric force is a conservative force, and therefore we will be able to define an electric potential energy.) Mathematically, these concepts can be defined in terms of integrals of force over a path.
The work done by a conservative force is independent of the path; in other words, the work done by a conservative force is the same for any path connecting two points:
\[W_{AB,\; path-1} = \int_{AB,\; path-1} \vec{F}_{cons} \cdotp d \vec{r} = W_{AB,\; path-2} = \int_{AB,\; path-2} \vec{F}_{cons} \cdotp d \vec{r} \ldotp \label{8.8}\]
The work done by a non-conservative force depends on the path taken. Equivalently, a force is conservative if the work it does around any closed path is zero:
\[W_{closed\; path} = \oint \vec{E}_{cons} \cdotp d \vec{r} = 0 \ldotp \label{8.9}\]
In Equation \ref{8.9}, we use the notation of a circle in the middle of the integral sign for a line integral over a closed path, a notation found in most physics and engineering texts.] Equations \ref{8.8} and \ref{8.9} are equivalent because any closed path is the sum of two paths: the first going from A to B, and the second going from B to A. The work done going along a path from B to A is the negative of the work done going along the same path from A to B, where A and B are any two points on the closed path:
\[\begin{split} 0 = \int \vec{F}_{cons} \cdotp d \vec{r} & = \int_{AB,\; path-1} \vec{F}_{cons} \cdotp d \vec{r} + \int_{BA,\; path-2} \vec{F}_{cons} \cdotp d \vec{r} \\ & = \int_{AB,\; path-1} \vec{F}_{cons} \cdotp d \vec{r} - \int_{AB,\; path-2} \vec{F}_{cons} \cdotp d \vec{r} = 0 \ldotp \end{split}\]
It is sometimes convenient to separate the case where the work done by non-conservative forces is zero, either because no such forces are assumed present or, like the normal force, they do zero work when the motion is parallel to the surface. Then
The mechanical energy of a particle does not change if all the non-conservative forces that may act on it do no work.
\[0 = W_{nc,\; AB} = \Delta (K + U)_{AB} = \Delta E_{AB} \ldotp \label{8.13}\]
In many cases, there exist systems for which Equation \ref{8.13} will hold exactly or approximately. In such situations, conservation of energy can be a powerful tool for understanding the behavior of the system.